Chae Seungmin

DevOps & carefree life [TMON] Channel Service Dev. Team

5 minute read

Map Simplification

  • k-map 을 이용한 간소화



Minterm 최소항

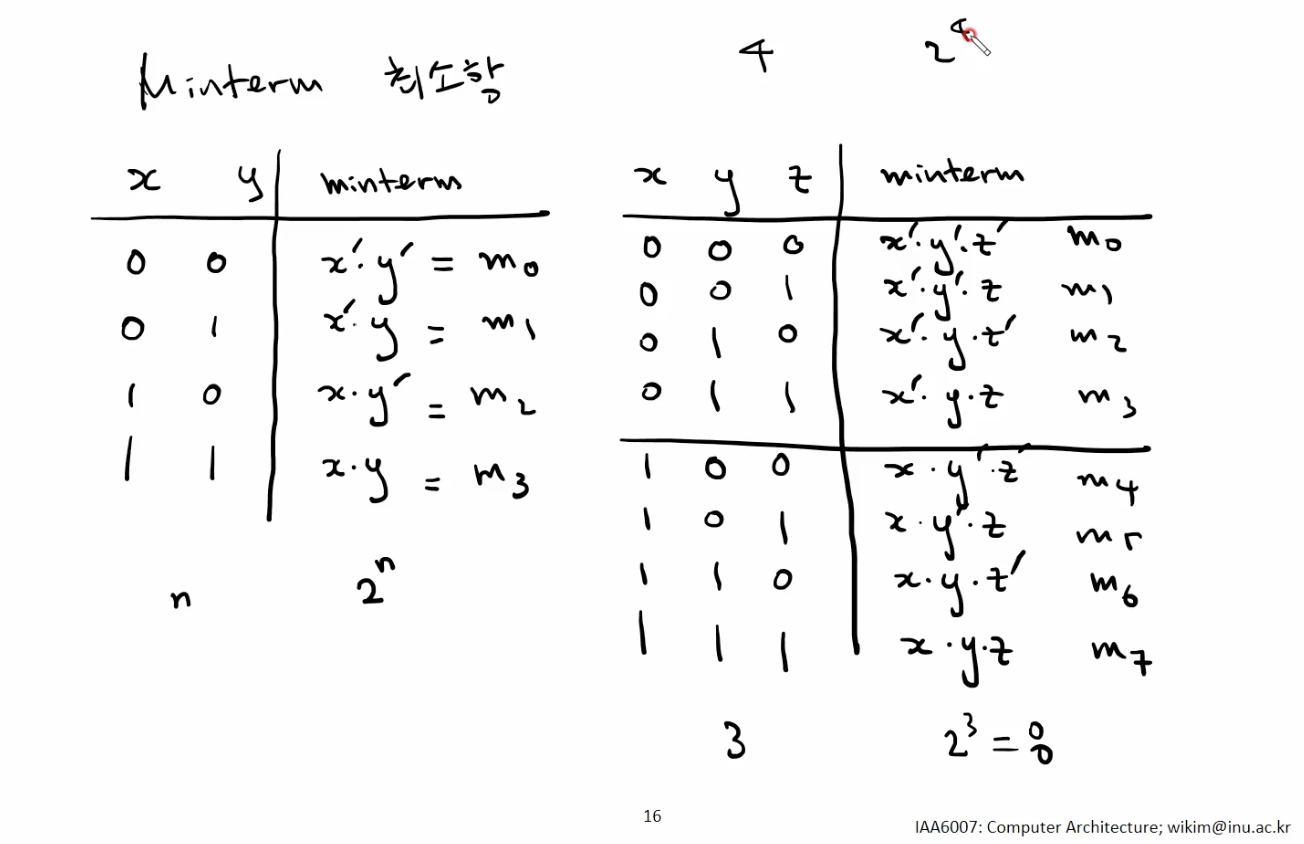
path 좌측: 2개 Input 에 대한 Minterm. 우측: 3개 Input 에 대한 Minterm.

Minterm: each combination of the variables

  • 모든 항이 들어가는 동시에 Input 을 1로 만들어주며 AND 만을 사용하는 조합
    • AND 연산이 사용되므로 0 은 NOT 으로 변환, 1은 그대로
    • 최소항에 대한 index는 0부터 시작하여 증가 (m0, m1, m2…)

  • 예시 (Function 을 Minterm 의 조합으로 변환)
    path
    • 모든 Input 이 각 항마다 존재해야 하므로 x + x’ = 1 임을 잘 활용하여 항 내에 존재하지 않는 Input 을 추가해준다.
    • Minterm 의 조합으로 나타낸 표현이므로 Sum of Minterm 이라고 한다. (= Canonical Form)
      • Sum of Minterm 의 표현 방법 세 가지
        • Equation : xy’z + xy’z’ …
        • Symbol : m0 + m1 + m2 …
        • Index : ∑(0, 1, 2, 4, 5, 6, 7)
  • 입력 개수와 Minterm 의 개수 간의 상관 관계
    • n variables -> 2^n minterms
  • Sum of Minterm 은 Sum of Product 의 특수한 형태.
    • 각 항이 Minterm 으로 이루어진 Sum of Product 형식.



Sum of Product (SOP) , Product of Sums(POS)

  1. Sum of Product (SOP)
    • F = y’ + xy + x’y’z’
      • 각 항은 OR 연산으로 구성.
      • 모든 항은 AND 로 연결되어 있음.

  2. Product of Sums (POS)
    • F = y’(x + y)(x’ + y’ + z’)
      • 각 항은 AND 연산으로 구성.
      • 모든 항은 OR 로 연결되어 있음.



Sum of Minterm (Canonical Form)

  • Sum of Product (SOP) 의 특수한 형태.
  • Canonical SOP 라고 할 수 있음.

path



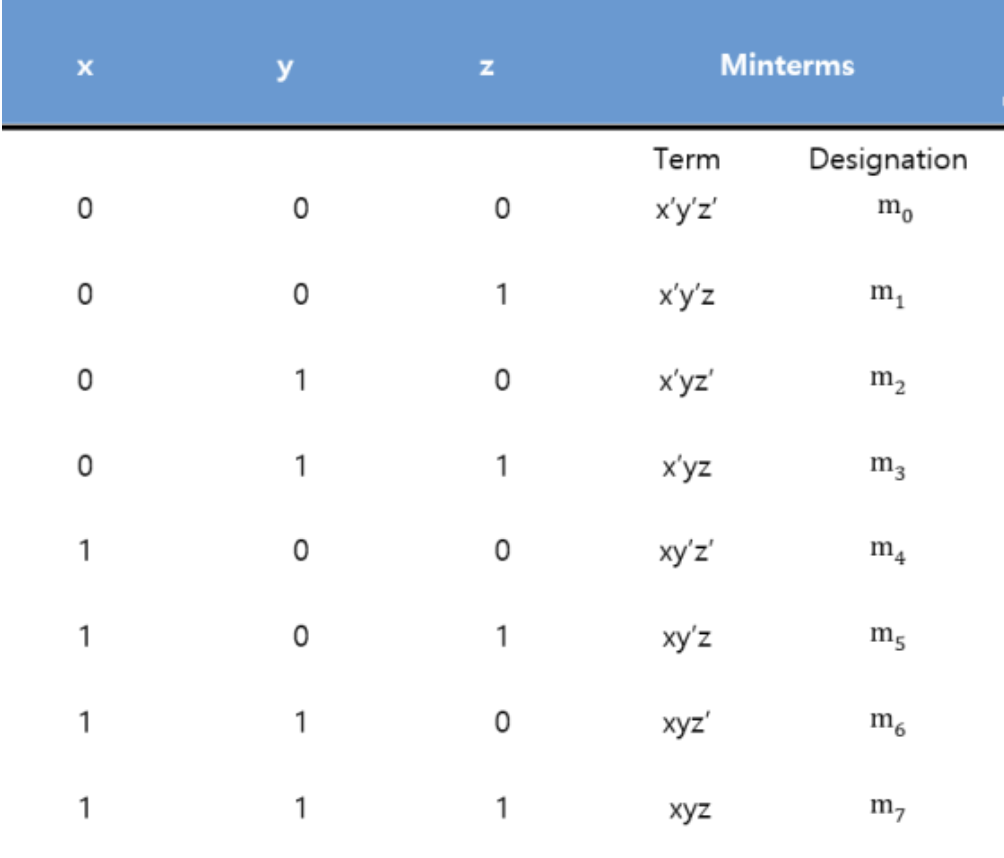
[기존 방법 - Sum of Minterm 구하기]

path

  1. 기존 수식을 Minterm 으로 변환.
    • x + x’ 은 항상 1 이므로 어디든 추가해서 사용 가능
  2. Minterm 으로 변환된 수식을 진리표에 따라 설정된 m (index) 으로 변환.
  3. 변환된 index으로 이루어진 수식을 sum 기호를 사용하여 마무리.



[쉬운 방법 - Sum of Minterm 구하기]

  1. F(Function) 의 진리표 구하기
  2. 해당 F 의 진리표 값이 1인 곳의 Minterm을 Sum 하면 끝.



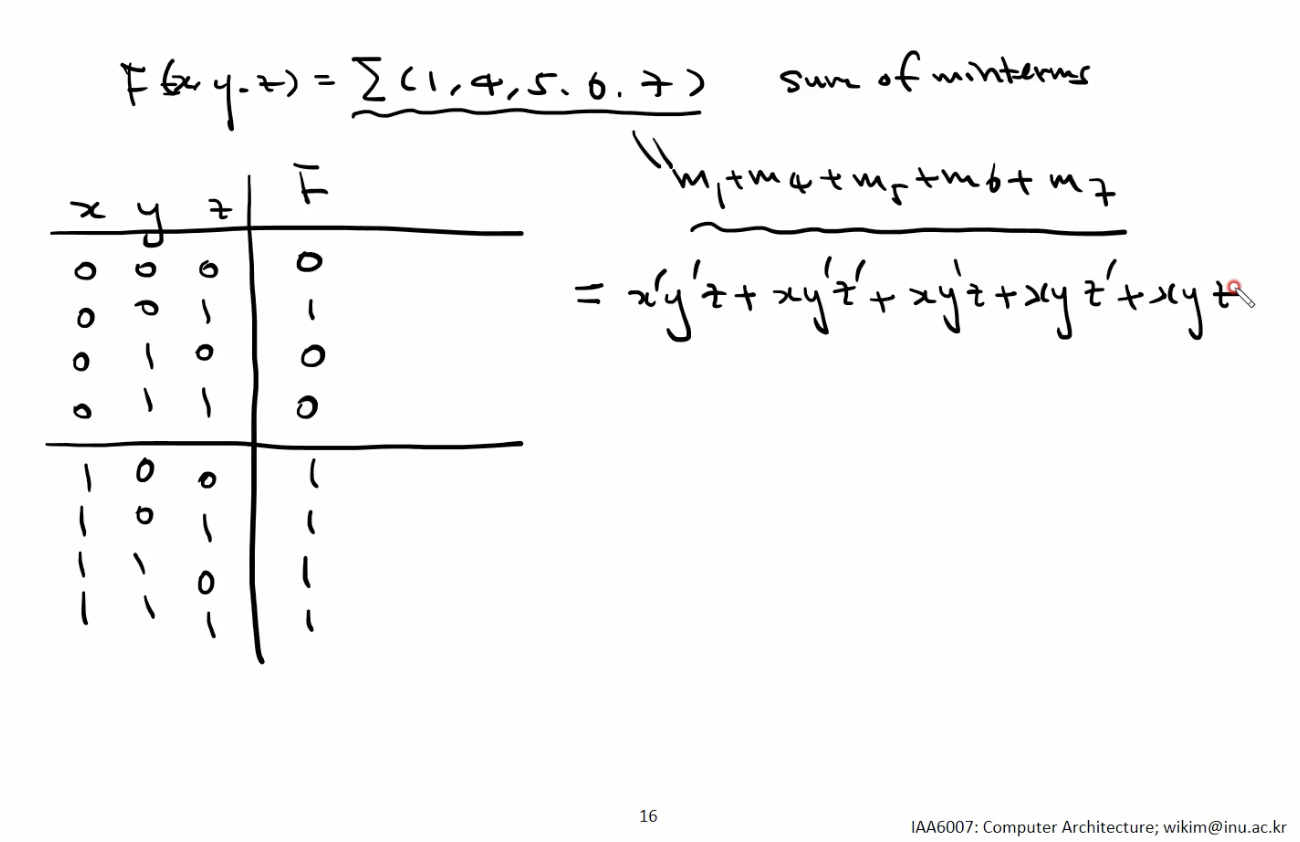
예시 1 (Function을 Sum of Minterm 으로 변환)

path

  • Function 의 진리표를 구한다.

    path
  • Function 의 진리표에서 1인 항들을 Sum.
  • Sum of Minterm 변환 끝.



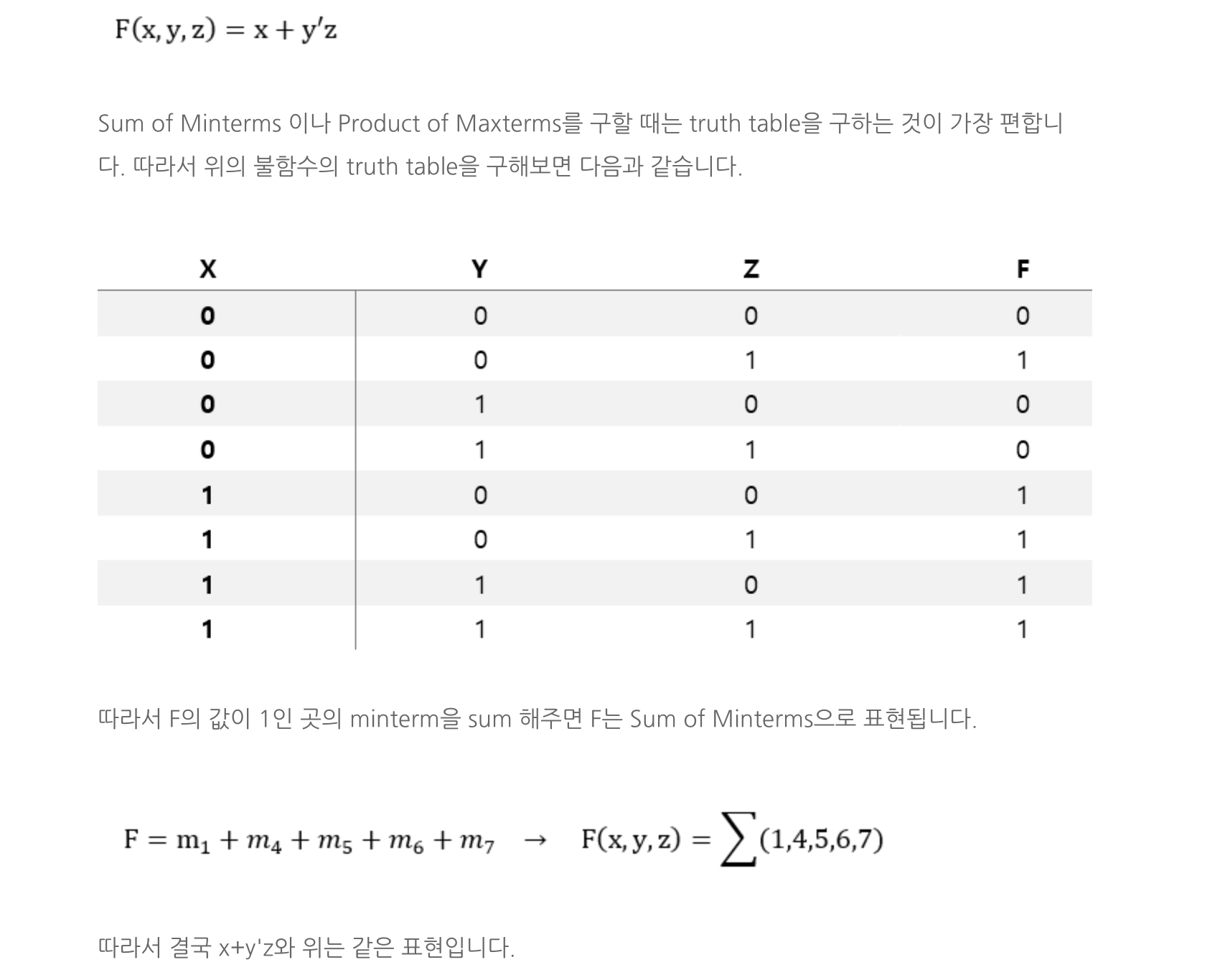
예시 2 (Sum of Minterm 을 Function 으로 변환)

path

  • Function 에 대한 진리표 구하기.
  • 해당 진리표에서 1인 항들을 Equation으로 표현.



참고 자료

path



카르노 맵 (Karnaugh map) 을 이용한 Boolean Function의 간소화

준비

  • Variables 및 Minterm 진리표



전체 모습 path



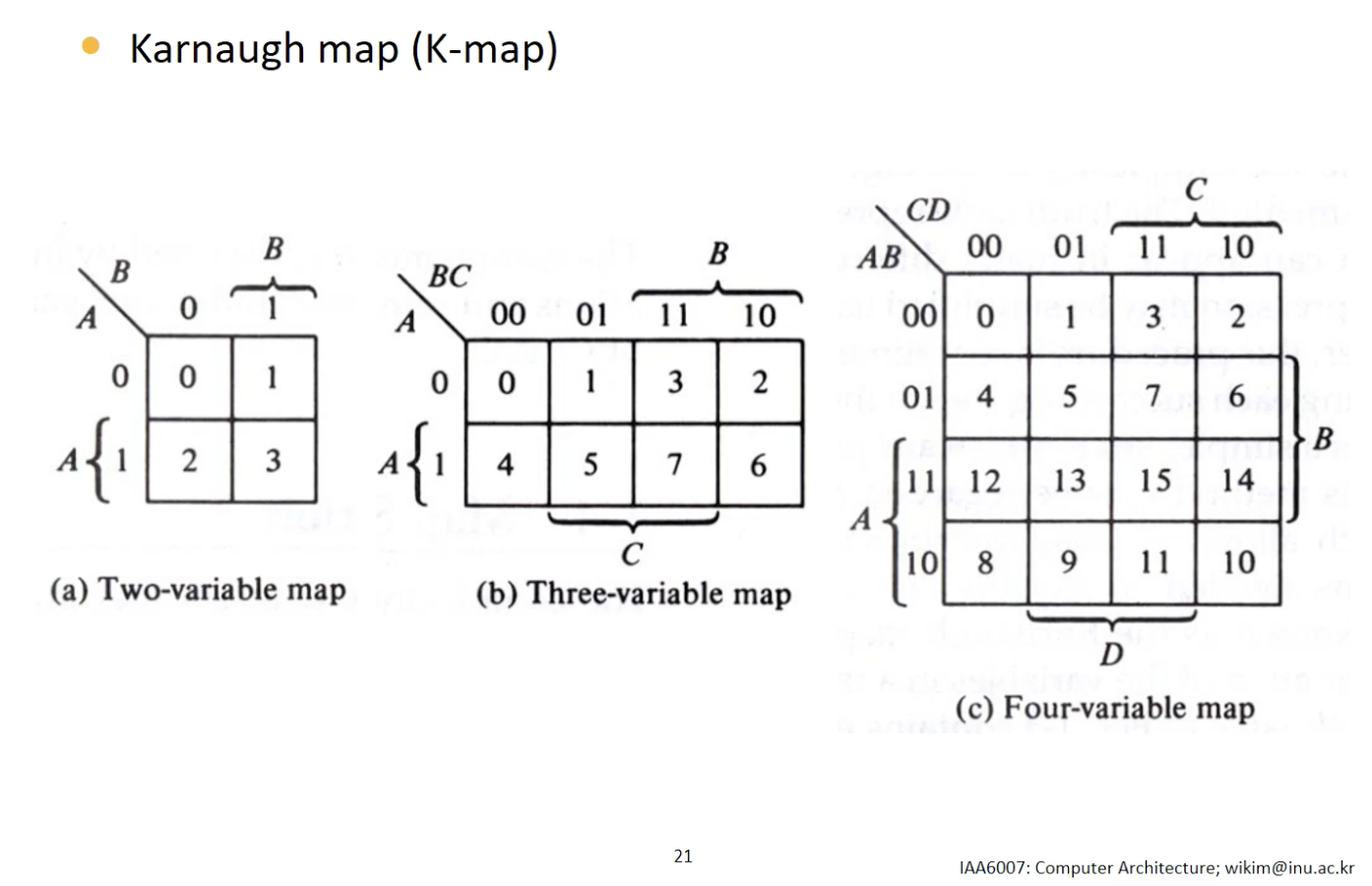
특징

  • Kmap 의 Cell 개수는 Minterm의 개수와 같다.



예시 (Variable 2개)

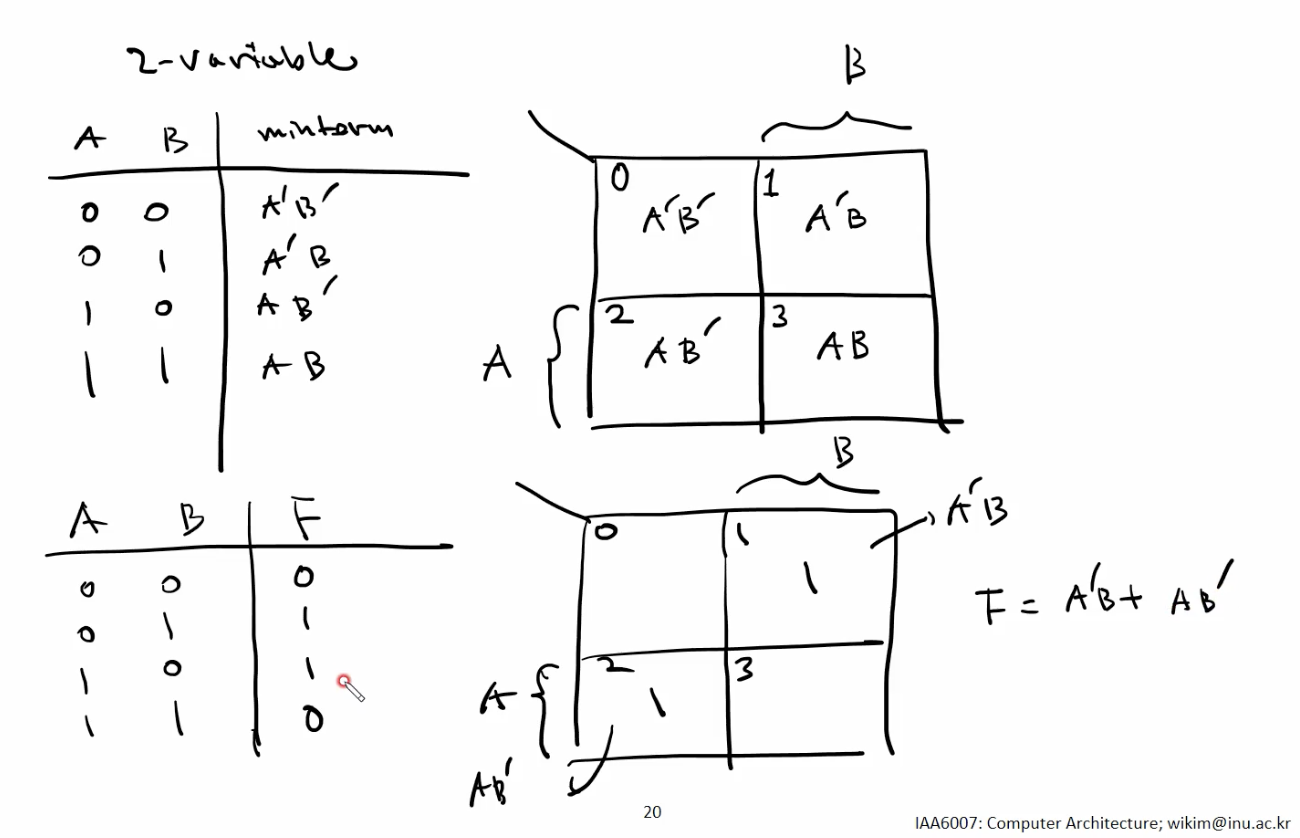
path 상단: K-map 기본 Frame / 하단: 예시

  • 두 개 Variable의 Minterm 진리표 구하기.
  • 해당 진리표를 참고하여 K-map 그리기.
  • 진리표와 K-map 을 참고하여 K-map 의 각 Cell 에 Indexing 하기.

    Ex)
  • 2개 Variable 에 대한 진리표 값이 1인 항의 Index 를 찾는다. (1, 2)
  • 해당 Index 를 가진 K-map 의 Cell 에 1 표시 및 Minterm 찾기. (A’B, AB’)



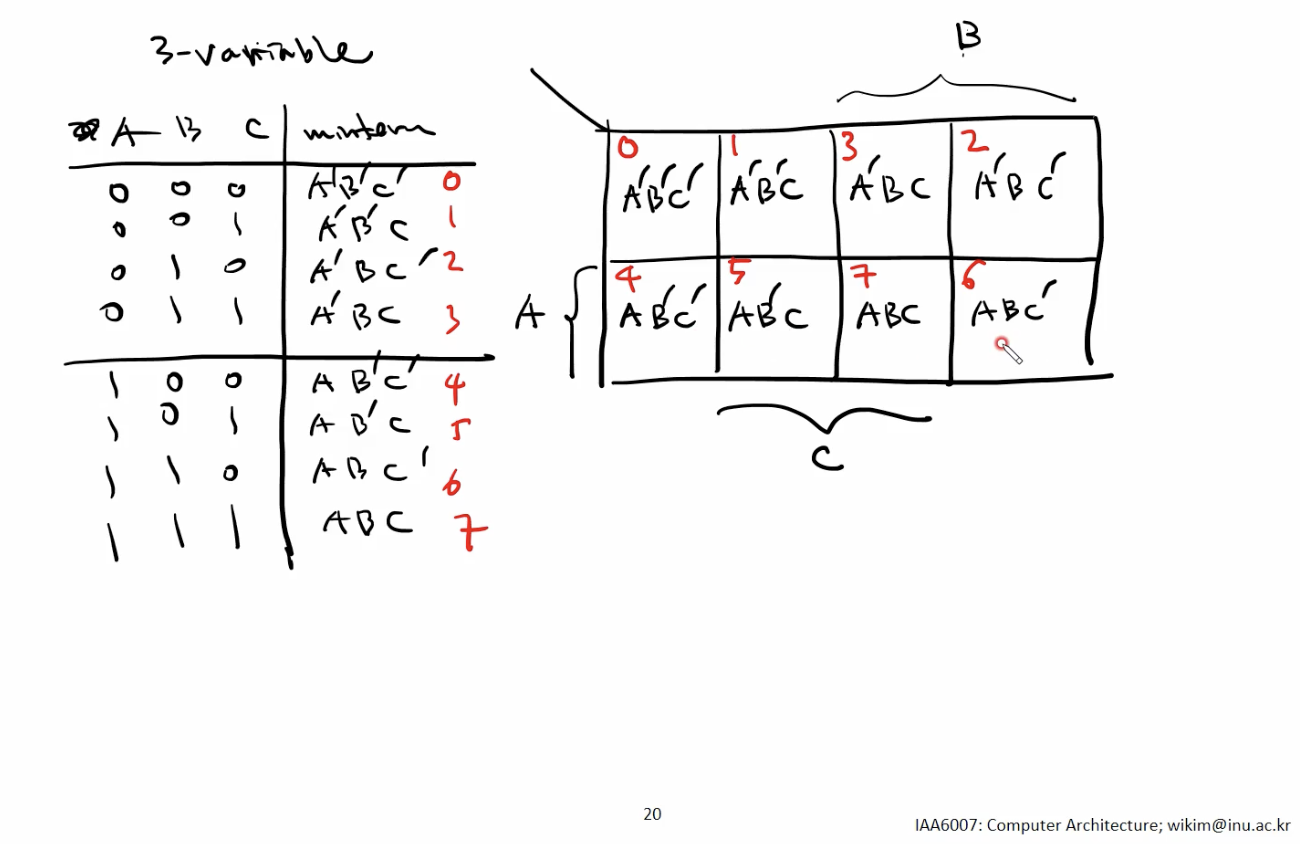
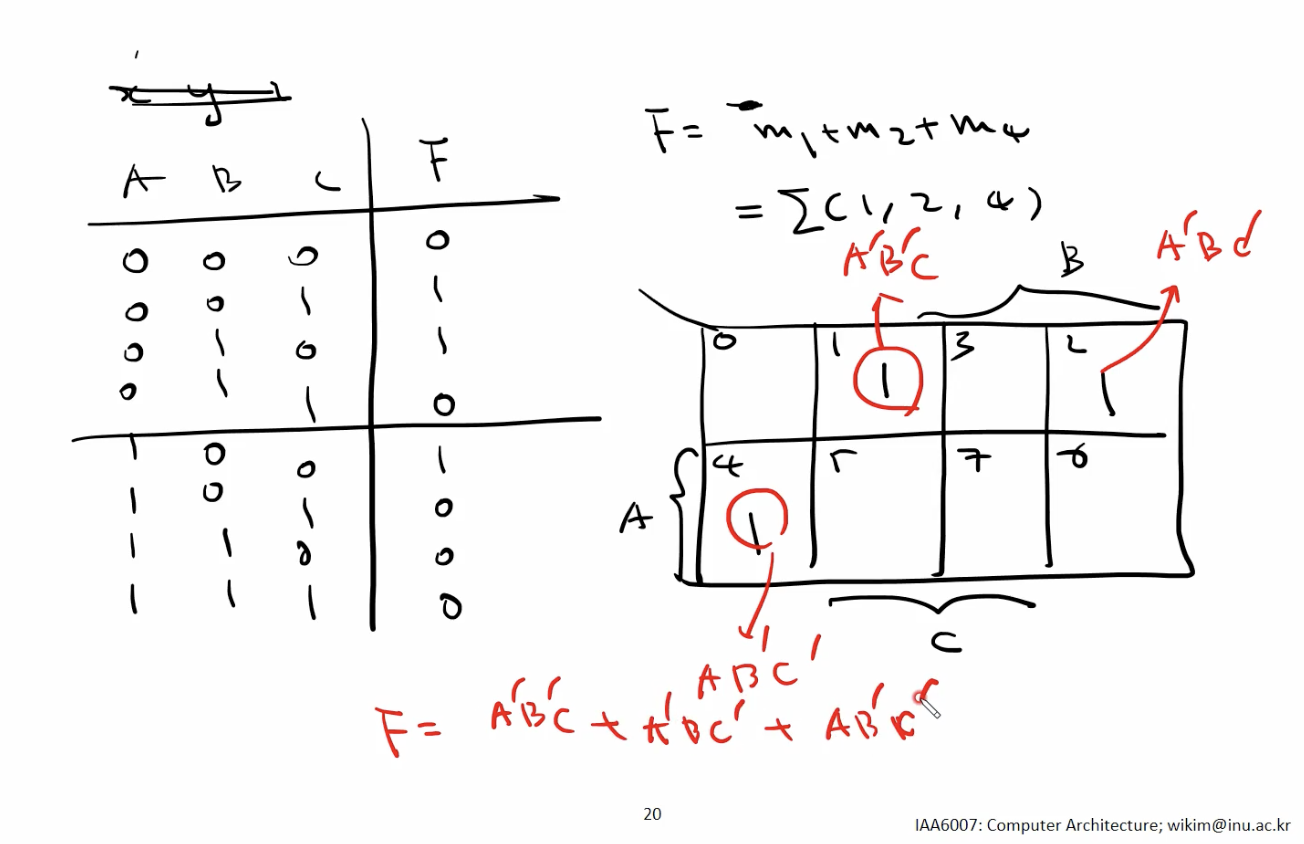
예시 (Variable 3개)

path

  • Variable 이 세 개인 경우 Kmap의 각 Cell에 대한 Indexing 순서 중요.
    0 , 1 , 3 , 2
    4 , 5 , 7 , 6

    Ex) (F = m1 + m2 + m4) path



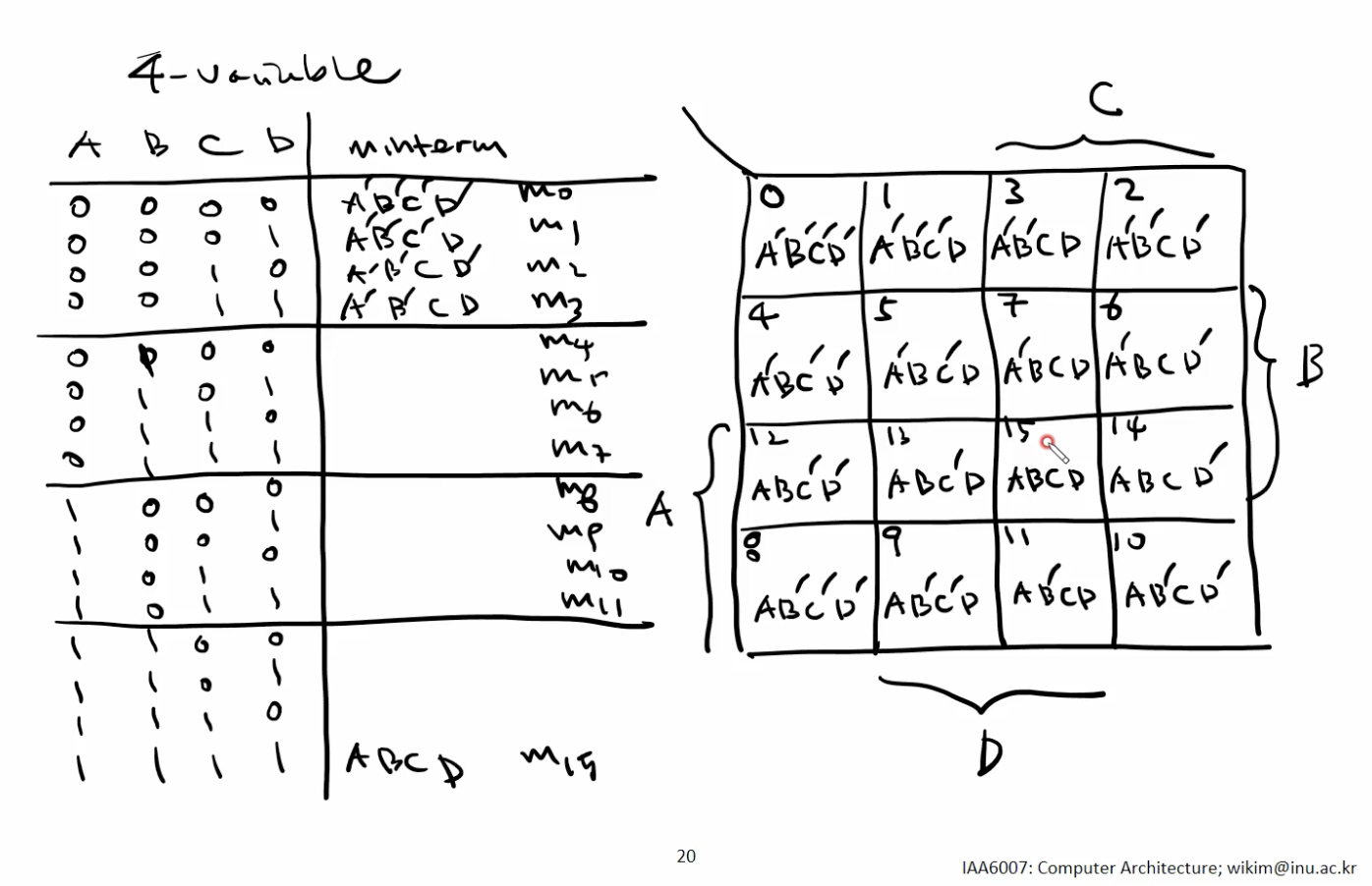
예시 (Variable 4개)

path

  • K-map Indexing 순서 확인



K-map 을 사용한 간소화
path

  • Cell 묶기 (각 Cell은 OR, + 로 연결됨)
    • 2 Cells
      • (m0, m1) → A’B’C’
      • 하나의 Variable 탈락 (3 Variables 로 간소화)
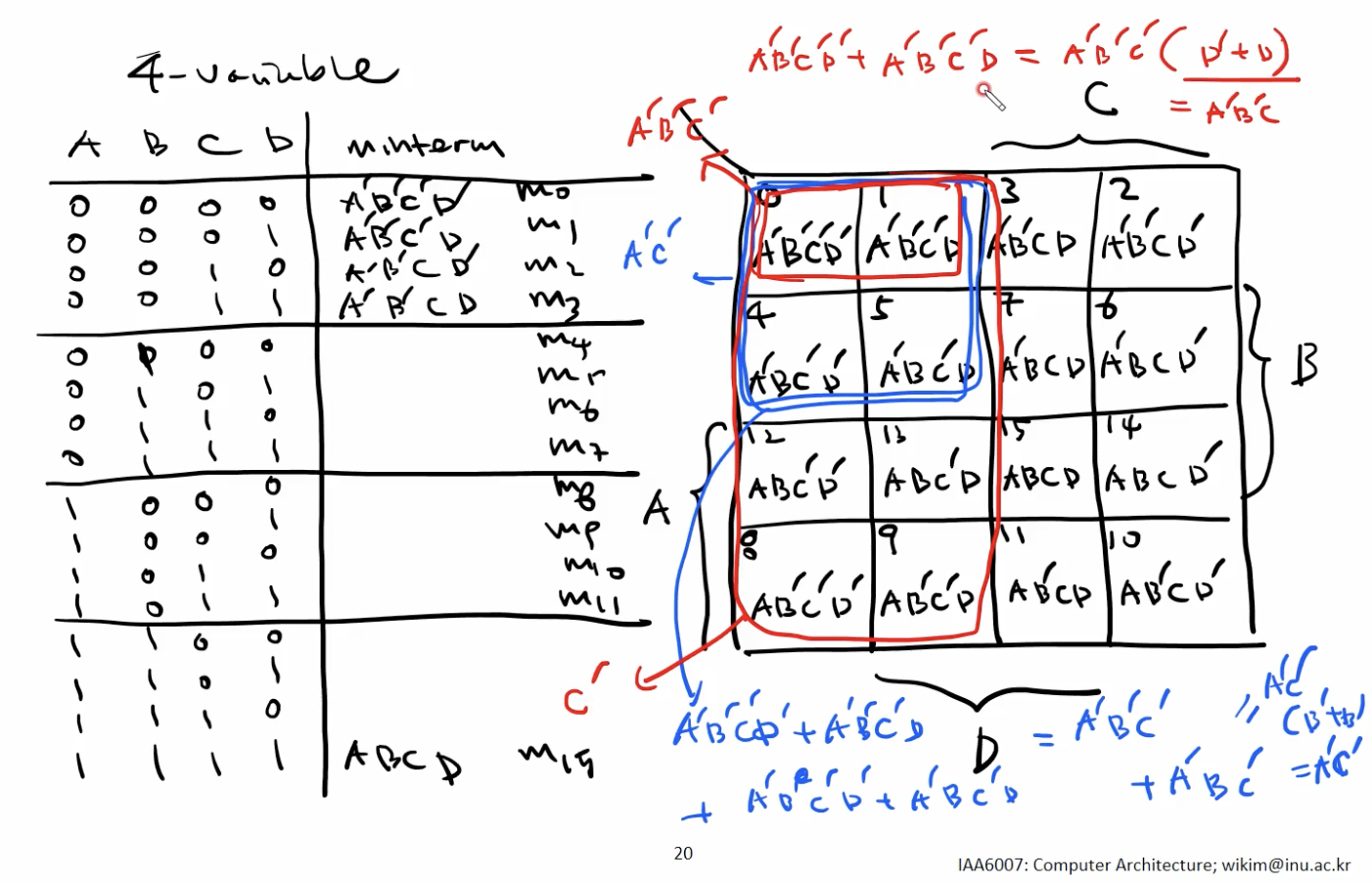
    • 4 Cells
      • (m0, m1, m4, m5) → A’C’
      • 두 개의 Variable 탈락 (2 Variables 로 간소화)
    • 8 Cells
      • (m0, m1, m4, m5, m12, m13, m8, m9) → C’
      • 세 개의 Variable 탈락 (1 Variables 로 간소화)

  • 결론
    • Cell 을 묶는 건 근접한 Cell 만 가능.
      • 근접: 변 (모서리X)
    • 2의 제곱 단위로 묶어야 한다. (2, 4, 8, …)
    • 묶을 때 Cell의 개수는 최대화, Group의 개수는 최소화
      • Cell 을 묶는 과정에서 중복되는 부분이 발생하더라도 최대화 하여 묶음.
    • Cell 을 묶을 시 K map 을 보았을 때 관련이 없어지는 Variable 은 제외가 되어 간소화 된다.
    • Kmap 을 사용한 간소화의 결과는 SOP 형식으로 반환된다.

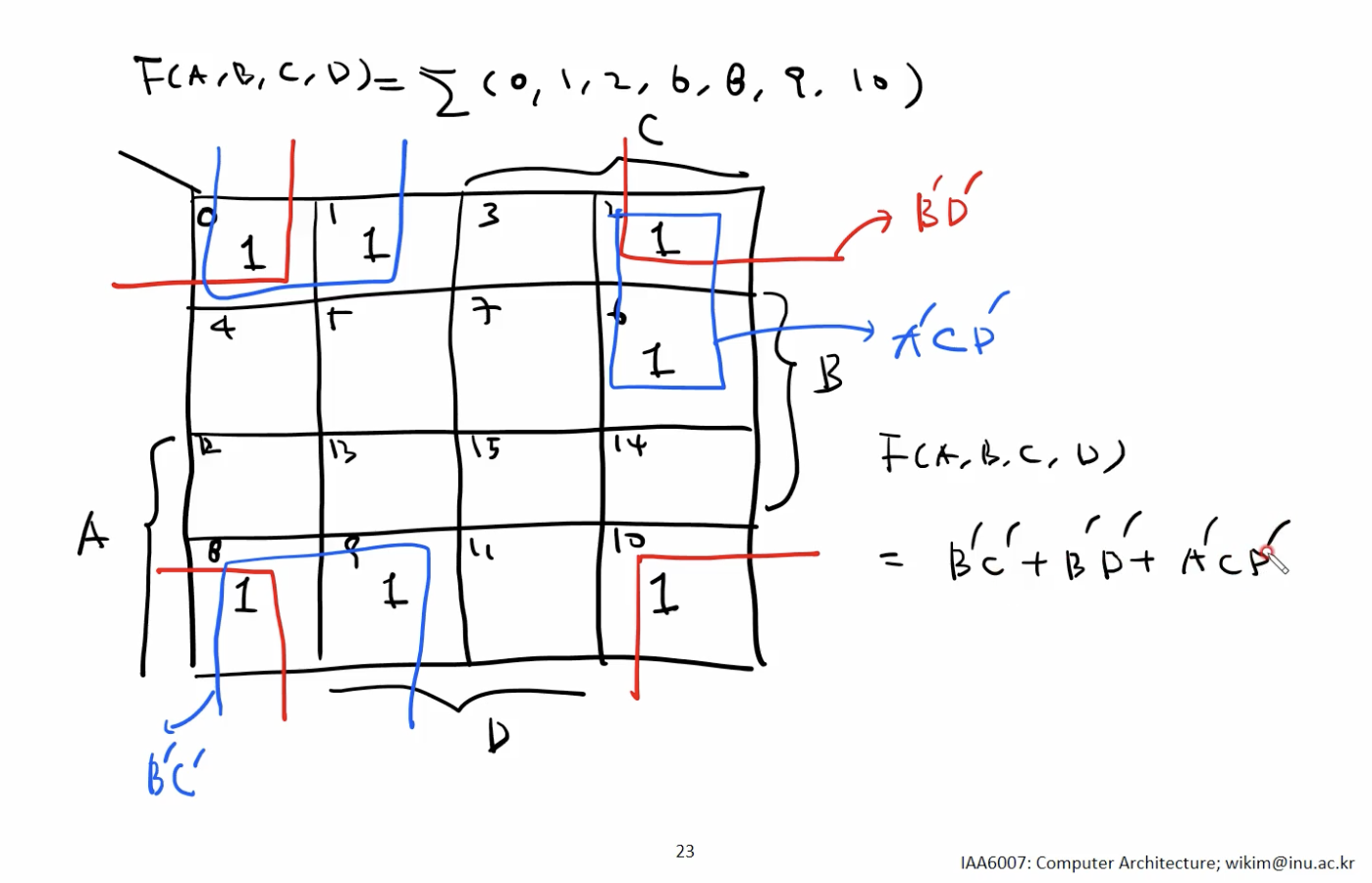
  • 예시 path
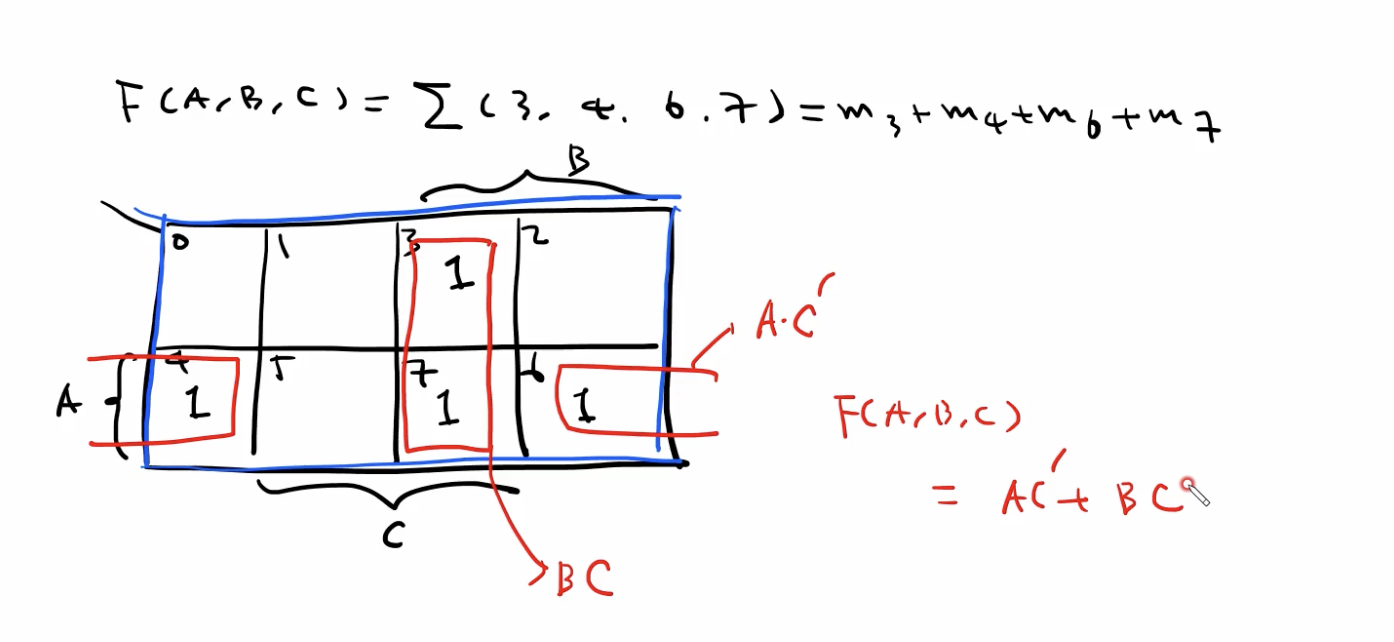
    • Input Variables: 3개

      path
    • Input Variables: 3개
    • 겹치는 부분이 발생하더라도 2의 제곱수 만큼 최대로 묶어야 한다.

      path
    • Input Variable: 4개
    • 마찬가지로 묶은 Cell 의 개수는 최대화, 그룹은 최소화 하여 묶기.



조금 다른 형태의 문제
path

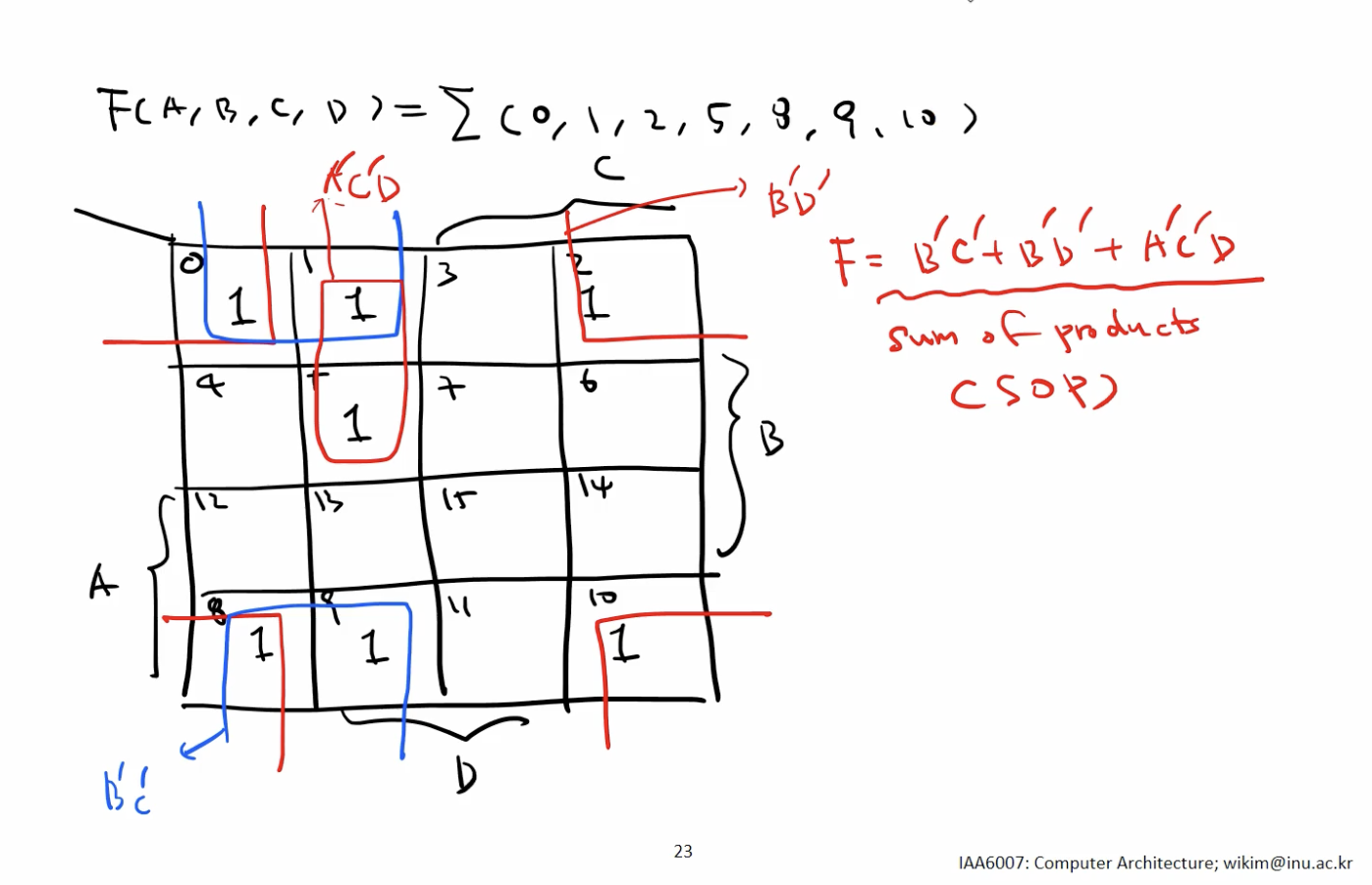
  • Kmap 을 사용한 간소화의 결과는 SOP 형식으로 반환된다.



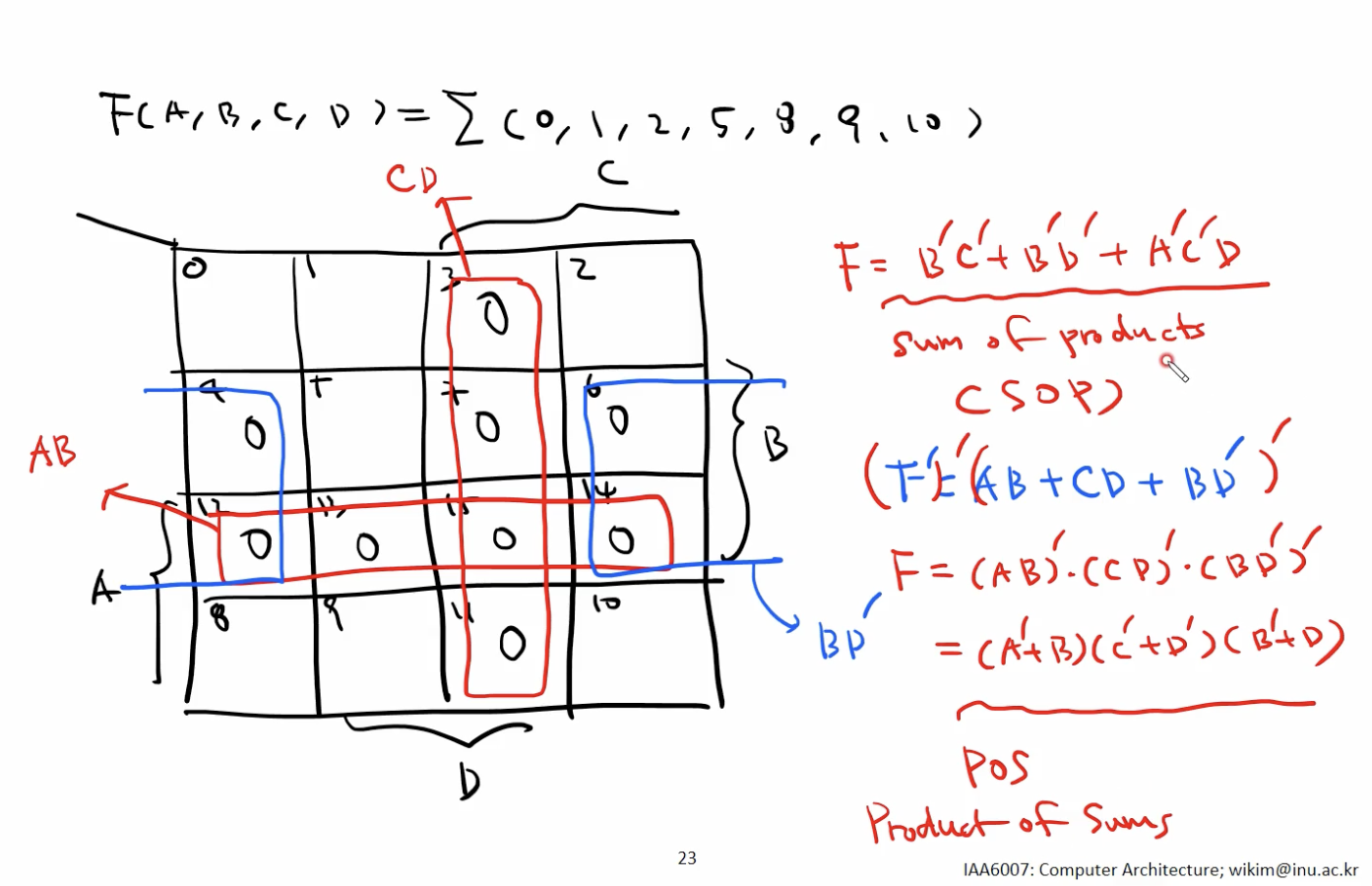
SOP -> POS 형식으로 변환하기
path

  • 위와 같이 Cell의 값이 1 이 아닌, 0인 항을 묶으면 된다. (= NOT F)
    • 우선 NOT F (= F’) 를 찾은 후 확인할 수 있는 SOP 형식에 다시 NOT 연산 실행.



SOP로 변환 후 NAND Gateway 만을 사용해서 다이어그램 그리기

  1. 기존 다이어그램 path

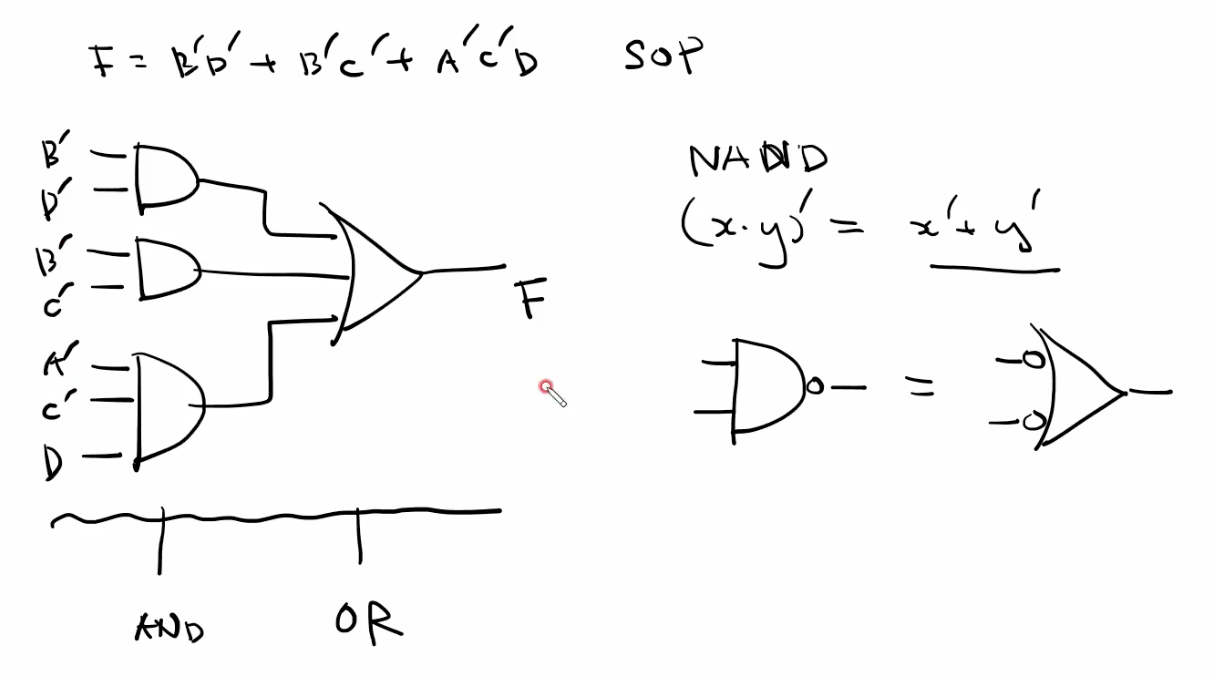
  2. NAND 만을 사용한 다이어그램 변환 path
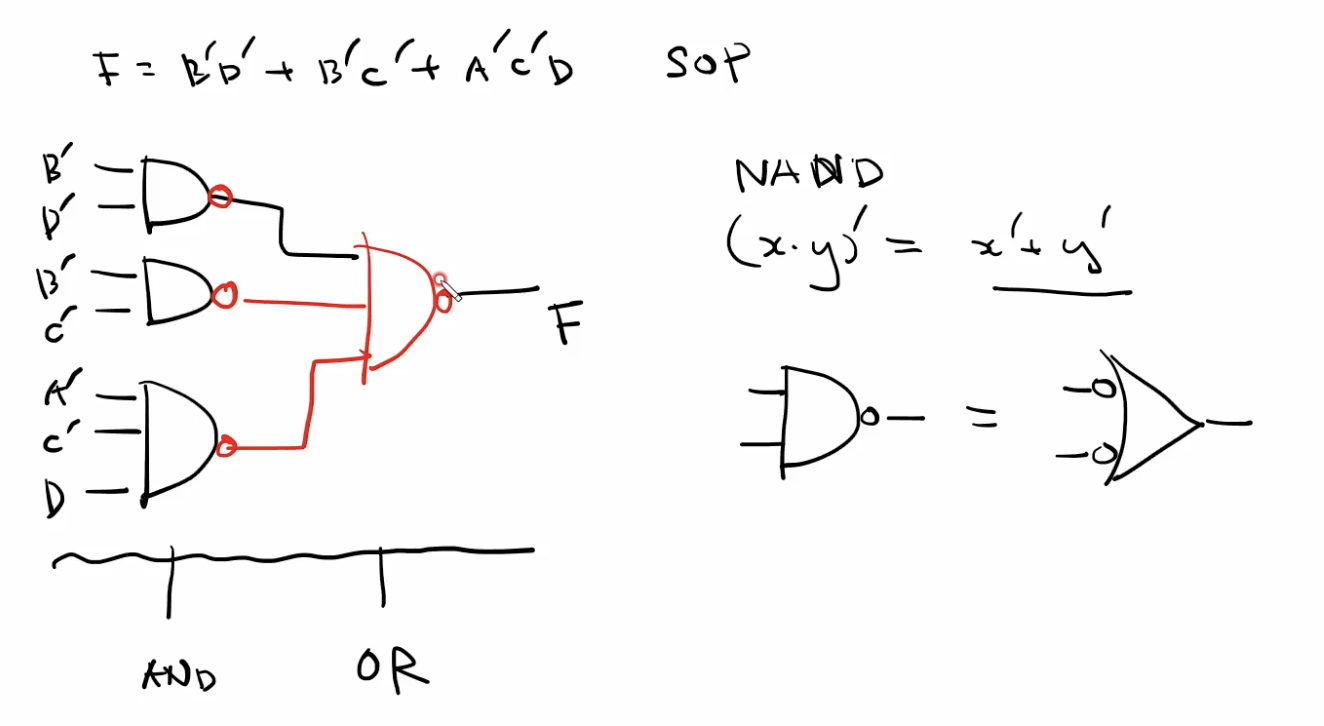
    • NOT 을 Inverter 앞 뒤에 추가하여 로직의 변경없이 NAND 만을 사용한 다이어그램으로 변환이 가능하다.



POS 변환 후 NOR Gateway 만을 사용해서 다이어그램 그리기

  1. 기존 다이어그램 path

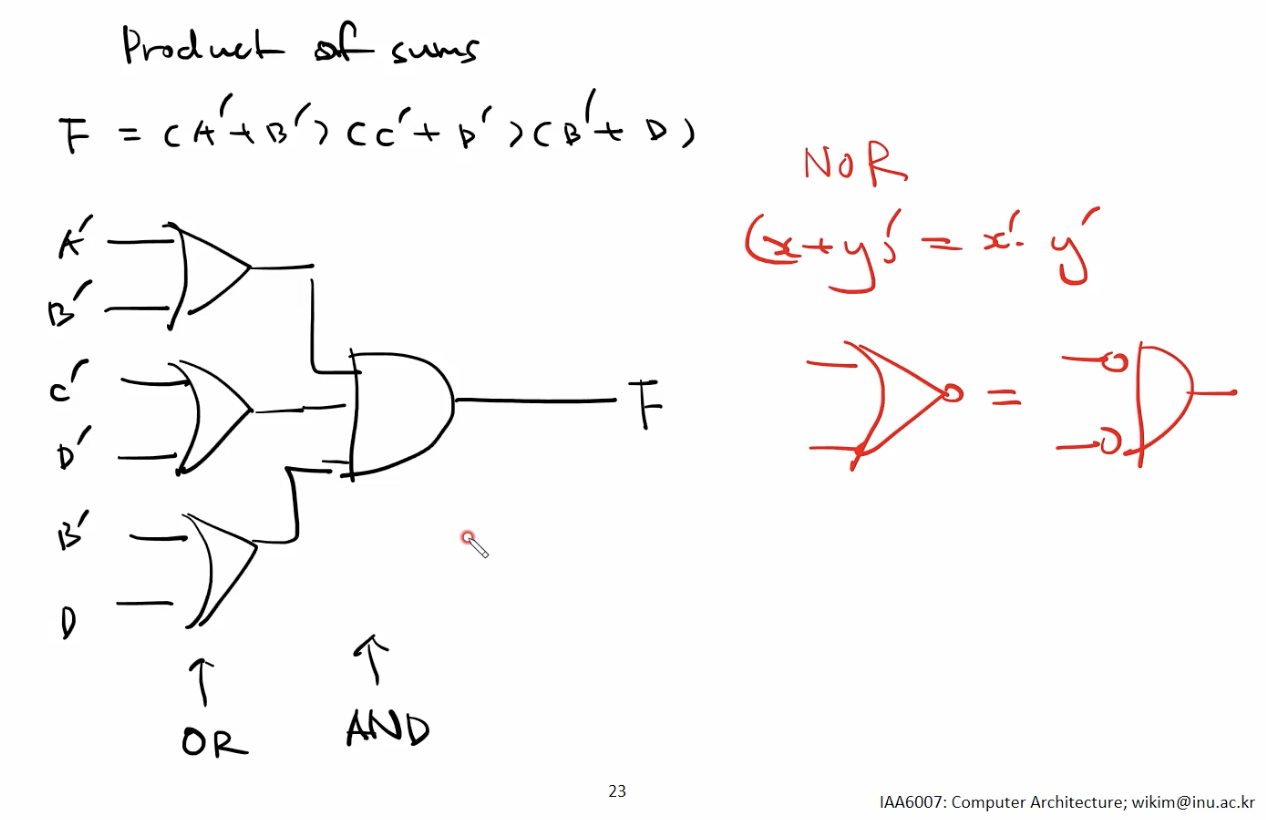
  2. NOR Gateway 만을 사용한 다이어그램 path
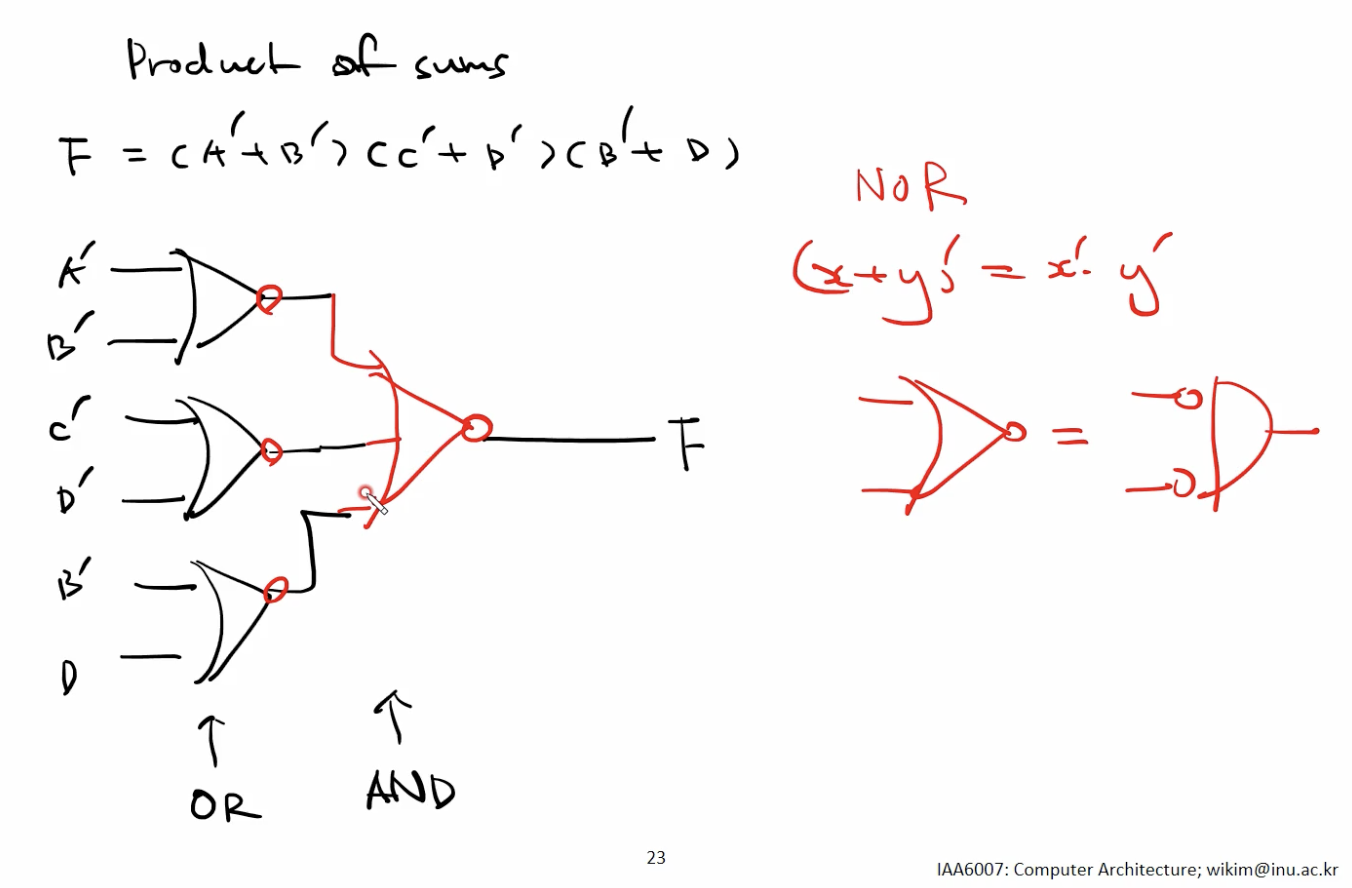
    • NOT 을 Inverter 앞 뒤에 추가하여 로직의 변경없이 NOR 만을 사용한 다이어그램으로 변환이 가능하다.



무관 조건 (Don’t care condition)

  • Function 에서 무관조건에 해당하는 Index는 0, 1 중 어떤 값이더라도 결과에 영향을 주지 않는다.
    • 어떤 값이어도 상관없는 항 (x로 표시)
    • 해당 항은 K-map값이 1인 항과 같이 묶을 수 있는 항.



문제 유형 1. SOP

path

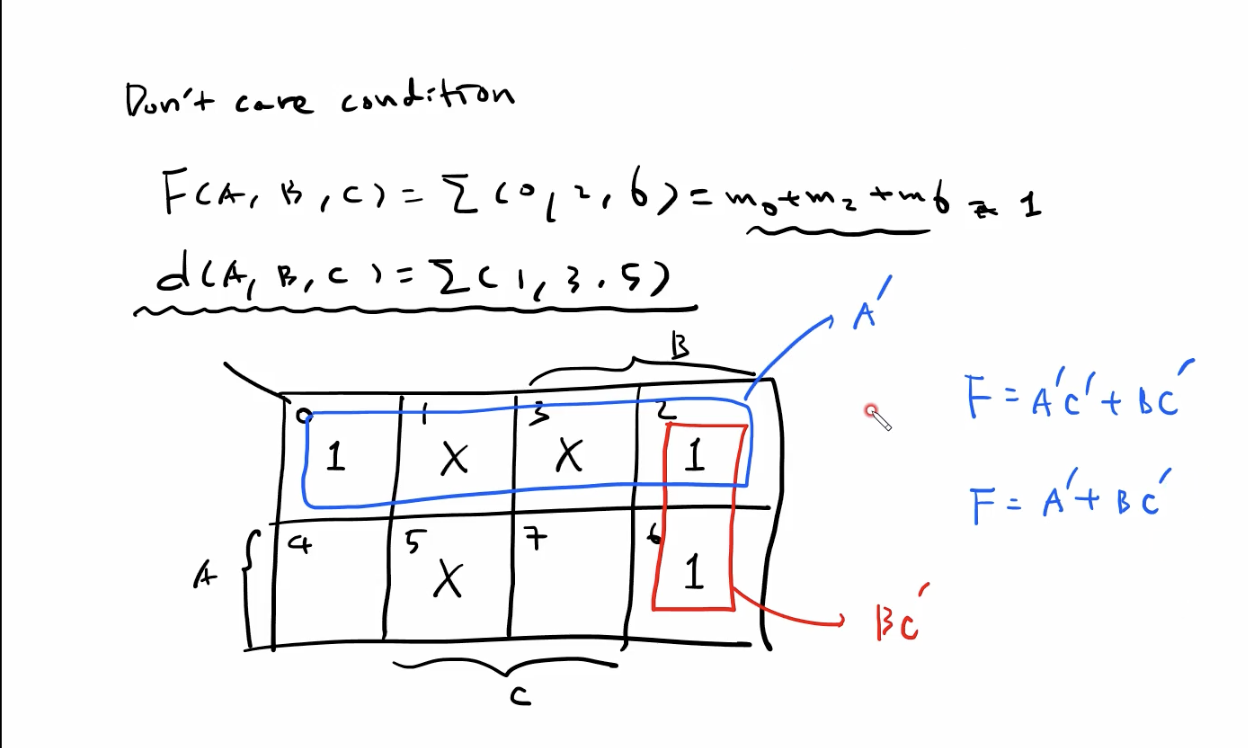
  • 항의 개수는 최대화 (2의 제곱값 기준, 무관조건 해당 항(x) 포함)
    • 무관 조건이 없던 기존의 경우 1의 값을 가진 Cell 만 묶음.
      • F = A’C’ + BC’
    • 무관 조건이 있는 경우 무관 조건인 Cell 까지 최대화 하여 묶음.
      • F = A’ + BC’
  • 그룹의 개수는 최소화 하여 K-map 작성.



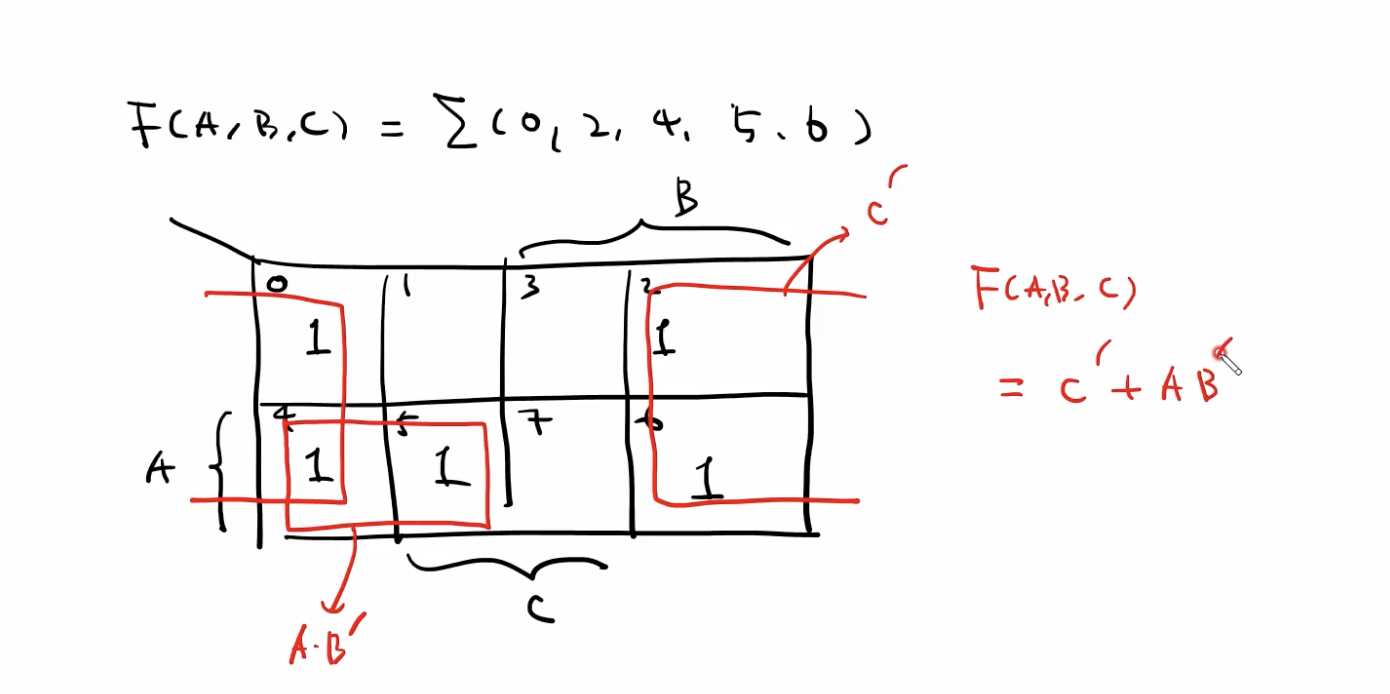
문제 유형 2. Equation

path

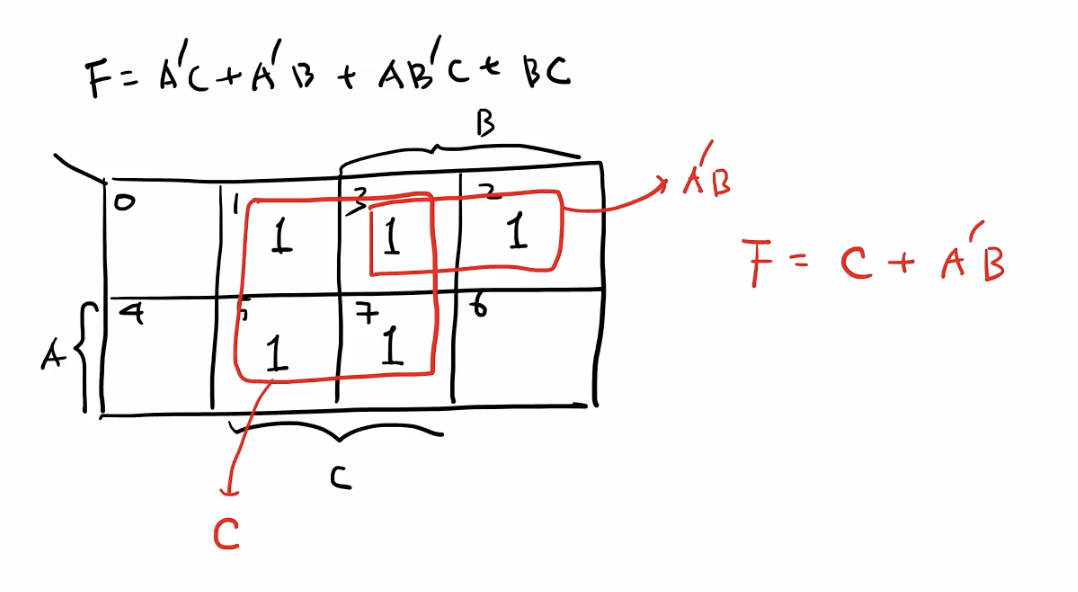
  • Equation 으로 문제가 주어졌을 시
    1. 변수의 개수 파악.
      • 3개 (A, B, C)
    2. 그에 맞는 카르노 맵 작성.
    3. 최대 항, 최소 그룹으로 묶어 간소화.
      • F = C + A’B



문제 유형 3. 간소화의 여러 가지 경우의 수 발생

1. 간소화 결과 Literal(변수) 이 4개 발생한 경우

path



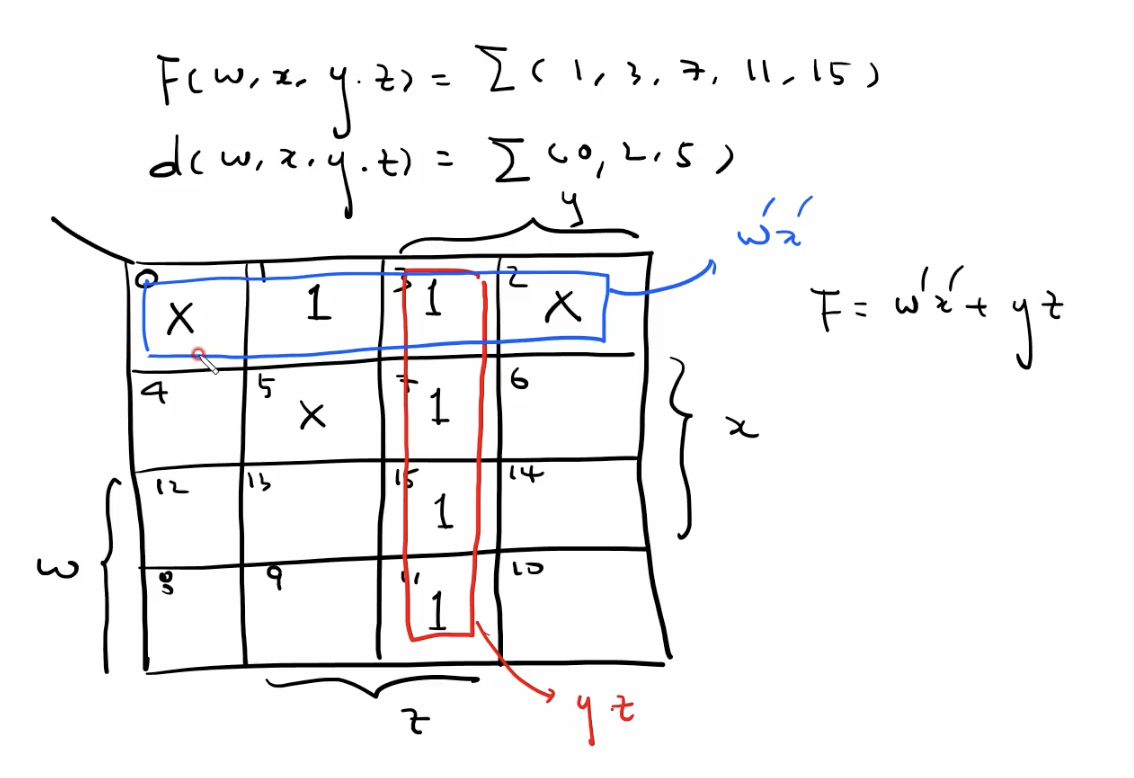
2. 간소화 결과 Literal(변수) 이 3개 발생한 경우

path

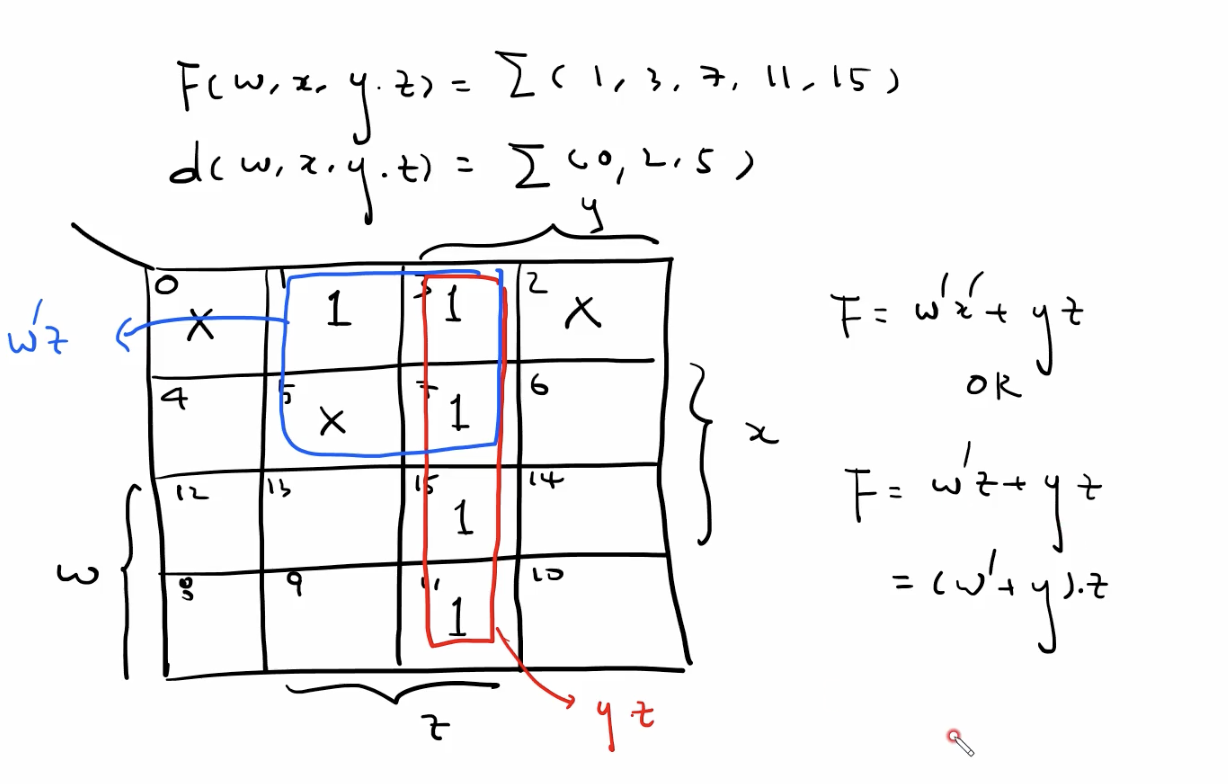
  • 위 예시처럼 여러 가지의 간소화 결과 발생 시 두 가지 답 모두 틀린 것은 아니다.
  • 하지만 Literal 개수 관점에서 더 적은 Literal 을 가진 결과가 더 잘 간소화 했다고 볼 수 있다.
    • 이 결과를 도출하기 위해 타 minterm 에서 이전에 이미 묶여졌던 항을 위주로 묶는다면 (예시 2번처럼) 결과 도출 시 공유하고 있는 변수가 많을 확률이 높아 다시 한번 간소화 가능.



지식 공유 및 기록을 위한 컴퓨터 구조 개인 학습 포스트입니다. 피드백은 항상 환영합니다! 긴 글 읽어주셔서 감사합니다.



처음으로~

Task Lists

  • Map Simplification
  • Minterm 최소항
  • Sum of Product (SOP) , Product of Sums(POS)
  • Sum of Minterm (Canonical Form)
  • [기존 방법 - Sum of Minterm 구하기]
  • [쉬운 방법 - Sum of Minterm 구하기]
  • 카르노 맵 (Karnaugh map) 을 이용한 Boolean Function의 간소화
  • 무관 조건 (Don’t care condition)
  • 문제 유형 1. SOP
  • 문제 유형 2. Equation
  • 문제 유형 3. 간소화의 여러 가지 경우의 수 발생

Comments

You May Also Enjoy