Finding Features - Scale, Rotation, View Point

---

Invariant Descriptors

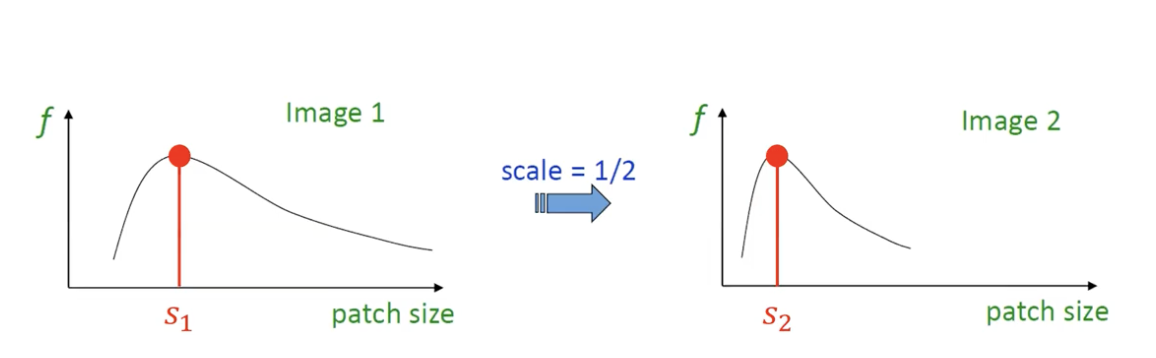
Scale

위와 같이 두 이미지를 다른 Scale 을 가지도록 Crop (Image patches) 하였을 때, Matching 을 위해 두 이미지가 같은 특징을 갖도록 하는 방법은?

• 가장 쉬운 방법은 Crop 된 이미지를 서로 동일한 특징을 갖도록 아래와 같이 Re-scale 하는 것.
  

Scale Changes 특징

Scale Change는 많은 시간이 소요됨.

• 모든 경우의 수를 전부 탐색 (Exhaustive Search), 두 개의 Crop 영역이 Matching이 되는지 확인해야함.
  
  

시간 복잡도

• O(N^2S)
  
  • N fearures perimage
    
  • S re-scalings per feature

해결 방법 : 스케일링 자동화 (Automatic Scale Selection)

Main Idea

• 특정 함수 작성
  
  • 각각의 Image Patch (Region) 의 입력을 받는 함수 작성.
    
    • Scale Invariant 한 함수.
      
    • 서로 대응되는 Patch 의 Scale이 다르더라도 입력이 되었을 때 같은 값을 반환 해주어야 함.
      
      • EX) Average Intensity
        
        
        • 두 Region 이 서로 다른 Scale을 가지더라도 유사한 평균 값을 가짐.

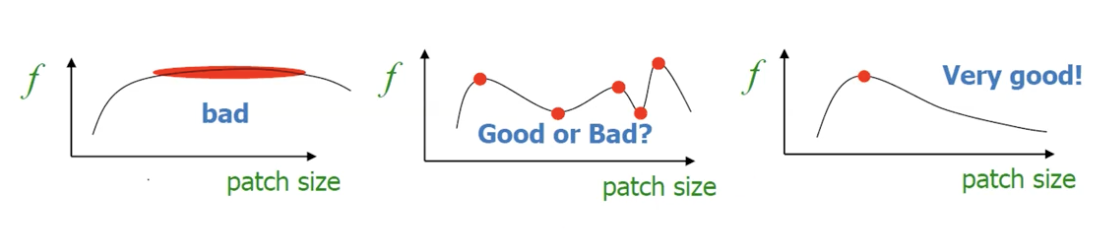
Automatic Scale Selection 을 하기 좋은 함수

좌표계에서 하나의 안정적이고 높은 Peak 가 존재 하는 경우.

• 여러 개의 Peak 가 존재하는 경우 ?
  
  • Peak가 많으면 적합한 Scale size를 찾기 어려울 수 있음.

Peak를 찾는 방법

기본적인 방법은 Edge 를 찾는 Kernel 을 Convolve 시키는 것.

• 좌표계에서 Peak (극 값) 를 찾는 것은 급격하게 변화하는 부분을 찾는것.
  
• 이는 마치 이전에 배웠던 Edge Detection 과 연관됨.
  

• Laplacian of Gaussian (LoG) Kernel 사용.
  • Gaussian 을 두 번 미분한 것.

Example : Automatic Scale Selection

1. Image 의 Scale을 키워나가며 그래프 생성
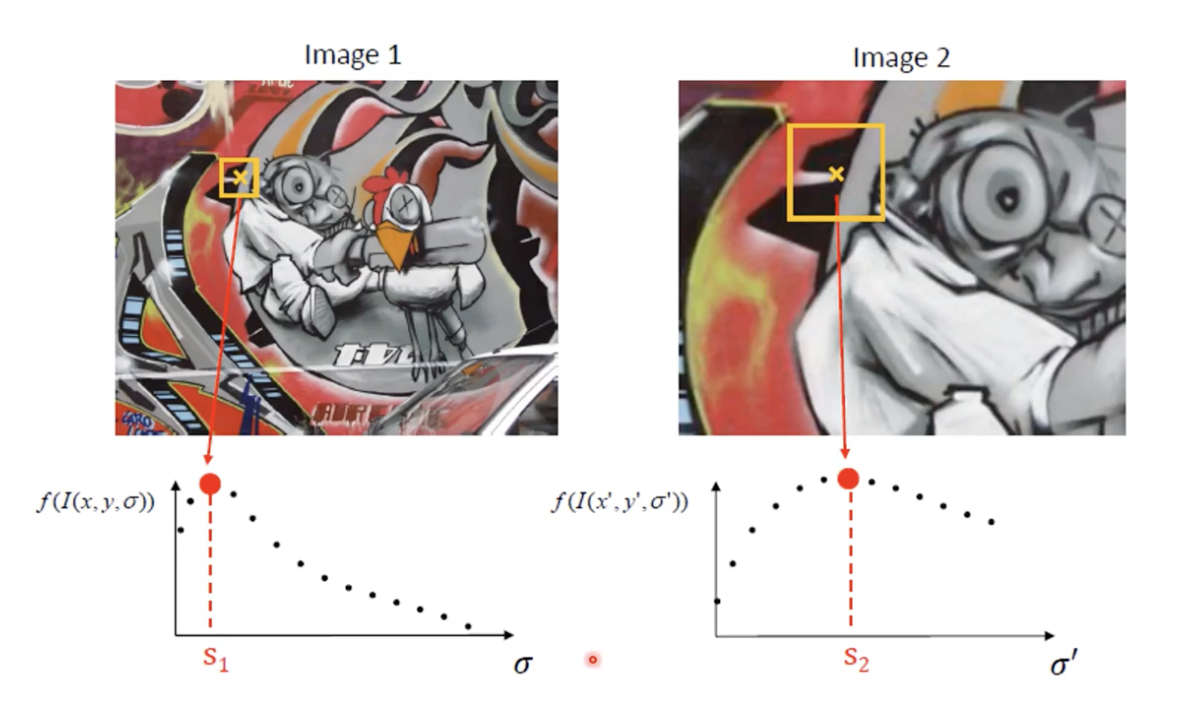
   • 적합한 Scale이 찾아지면 x, y 좌표계로 가져와서 적절한 크기로 Noramalize 한다.
2. 이후 해당 Patch 들을 SSD 로 Matching 시켜준다.
3. 마지막으로 Warping 을 통해 Patch Normalization을 완료한다.
   
   

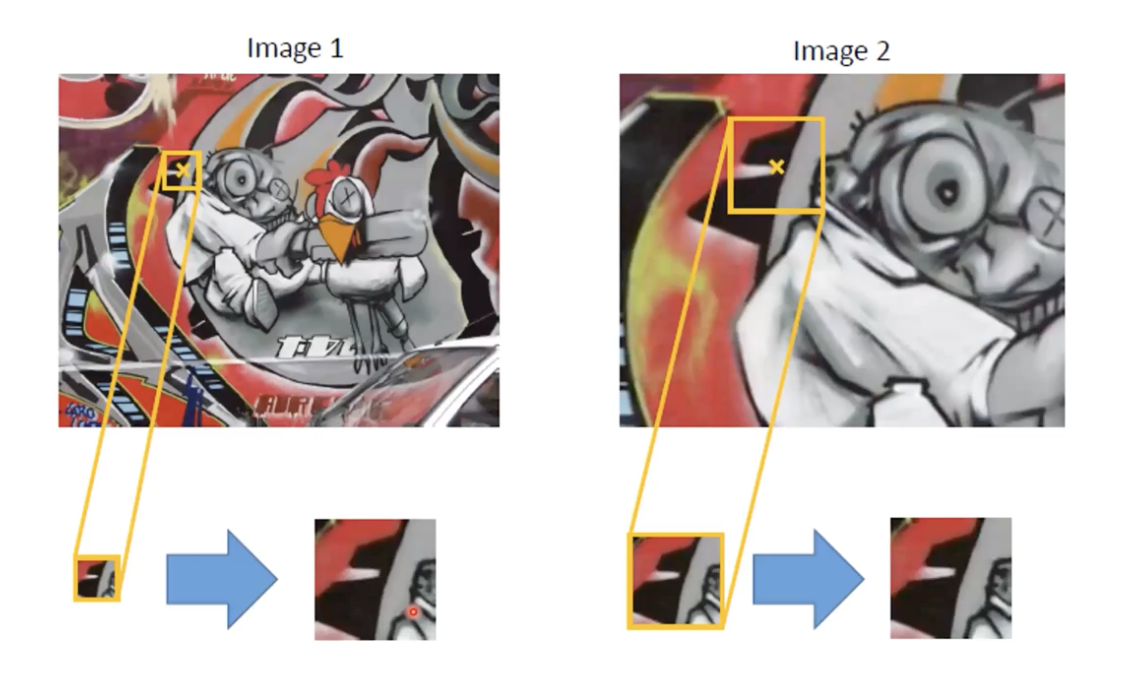
Rotation

어떻게 Rotation의 강인한 (Invariant) Descriptor 를 만들 수 있는가?

• Edge 에서 확인했던 Harris Detector (M Matrix of Harris) 사용.
  
  1. M Matrix of Harris 에서 주요한 방향 (Dominant gradient direction) 을 찾는다.
     
  2. Warping 을 통해 좌표계로 옮겨 올 수 있다.
     
     

HoG (Histogram of Gradient) descriptor

1. 각각의 Image에 대하여 Gradient 계산.
   
2. 해당 Gradient 에 대한 Histogram 작성.
   
3. 각 이미지의 Gradient 방향을 그래프로 보여줌.
   
   • = 주요한 방향 (Dominant Gradient) 을 찾을 수 있음.
     
4. 찾은 Hog Descriptor 를 나열하여 Concatination. (결합)

Patch 의 Orientation을 계산하는 방법.

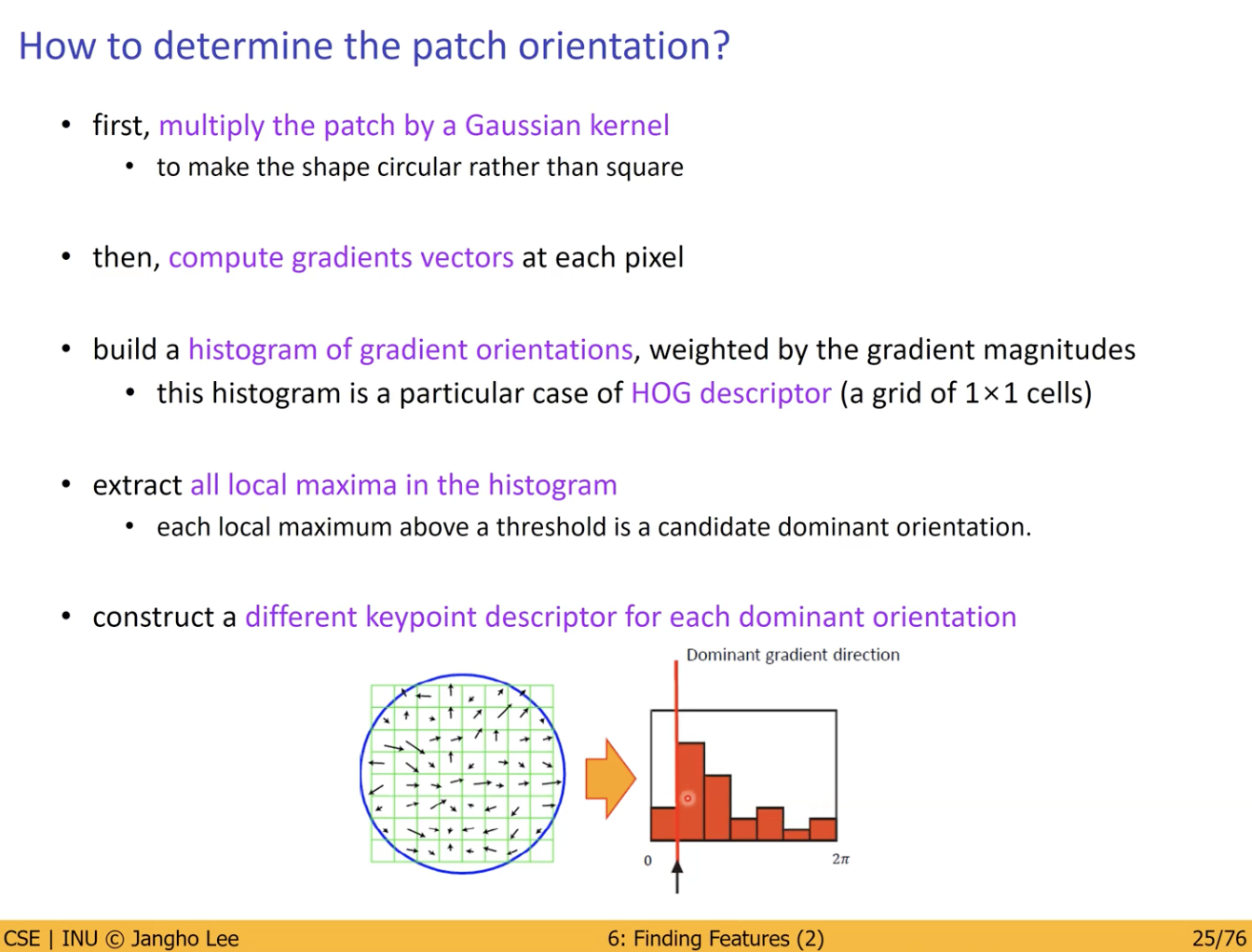
1. Gaussian Kernel을 이용하여 전체적 이미지를 Blurr 하게 만들어 준다. (전처리 과정)
2. Edge - Gradient Vector 를 계산
3. 좌표계의 구간 (Bean) 정하기
4. Gradient 에 Orientation이 얼마나 존재하는 지를 Histogram 을 통해 나타냄.
5. Histogram 의 Local Maxima를 계산.
6. 특정 방향으로 Patch가 Dominant 하게 되어있다는 것 확인.
7. Image Warping 실행 -> Rotation의 Invariant 한 속성들을 구할 수 있다.

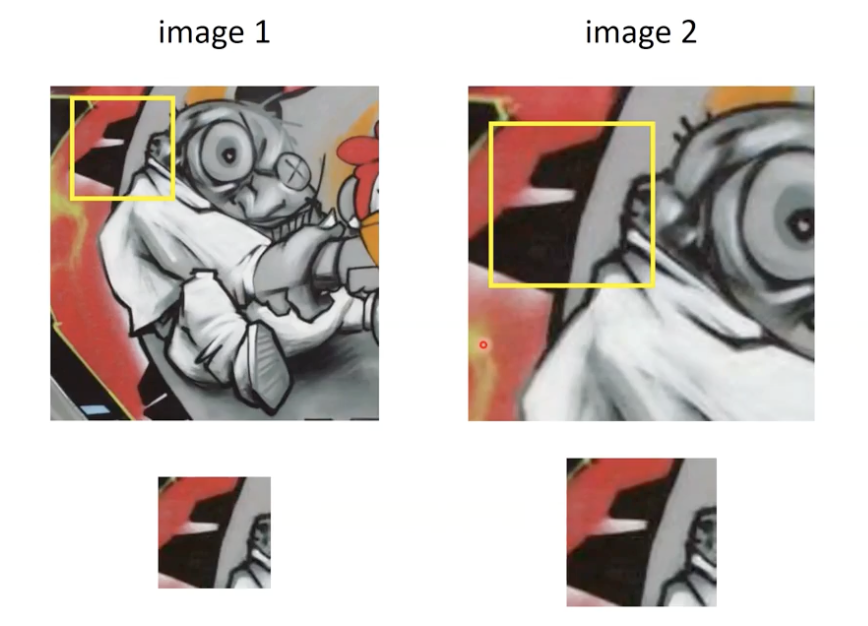
View Point

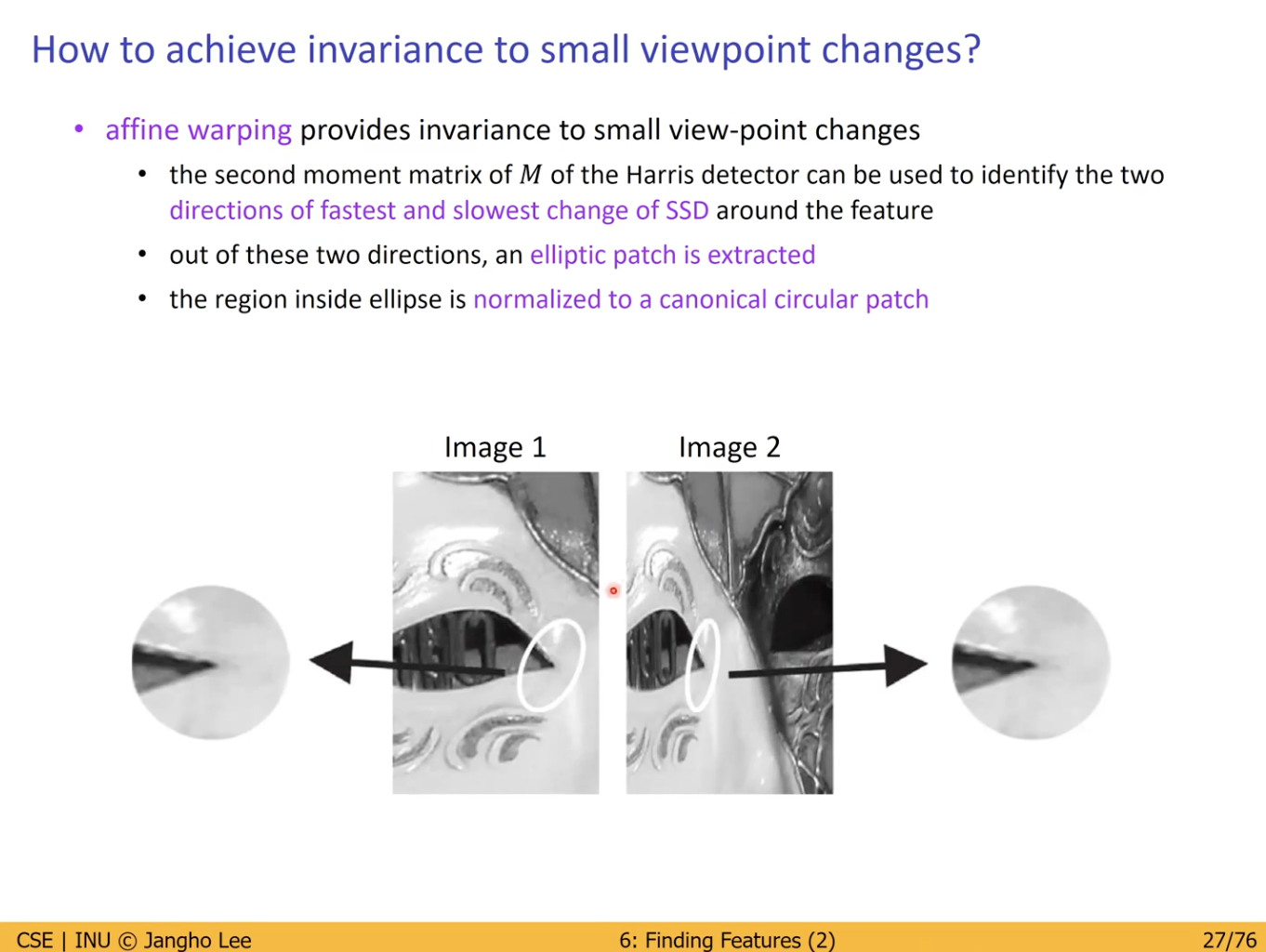
Image 1

• 상대적으로 펼쳐져 있는 이미지.
  

Image 2

• 볼 수 있는 Receptive 한 영역이 넓음.
  
• 넓은 이미지를 작은 공간에 두어 찌그러져 있는 상태.
  
  이러한 상황에서 Viewpoint 가 Invariant 하기 위해서는 Affine Warping 의 과정이 필요.

Affine Warping

Warping

• 일반적으로 이미지를 변형 시키는 것을 뜻함.
  
• Affine Transform
  
  Interpolation
  
• Warping 대상 픽셀과 인접한 픽셀들의 관계를 이용하여 Warping.
  
  
• Interpolation 의 세 가지 기법
  
  • Nearest neighbor interpolation
    
  • Bilinear interpolation
    
  • Bicubic interpolation

Warping Function

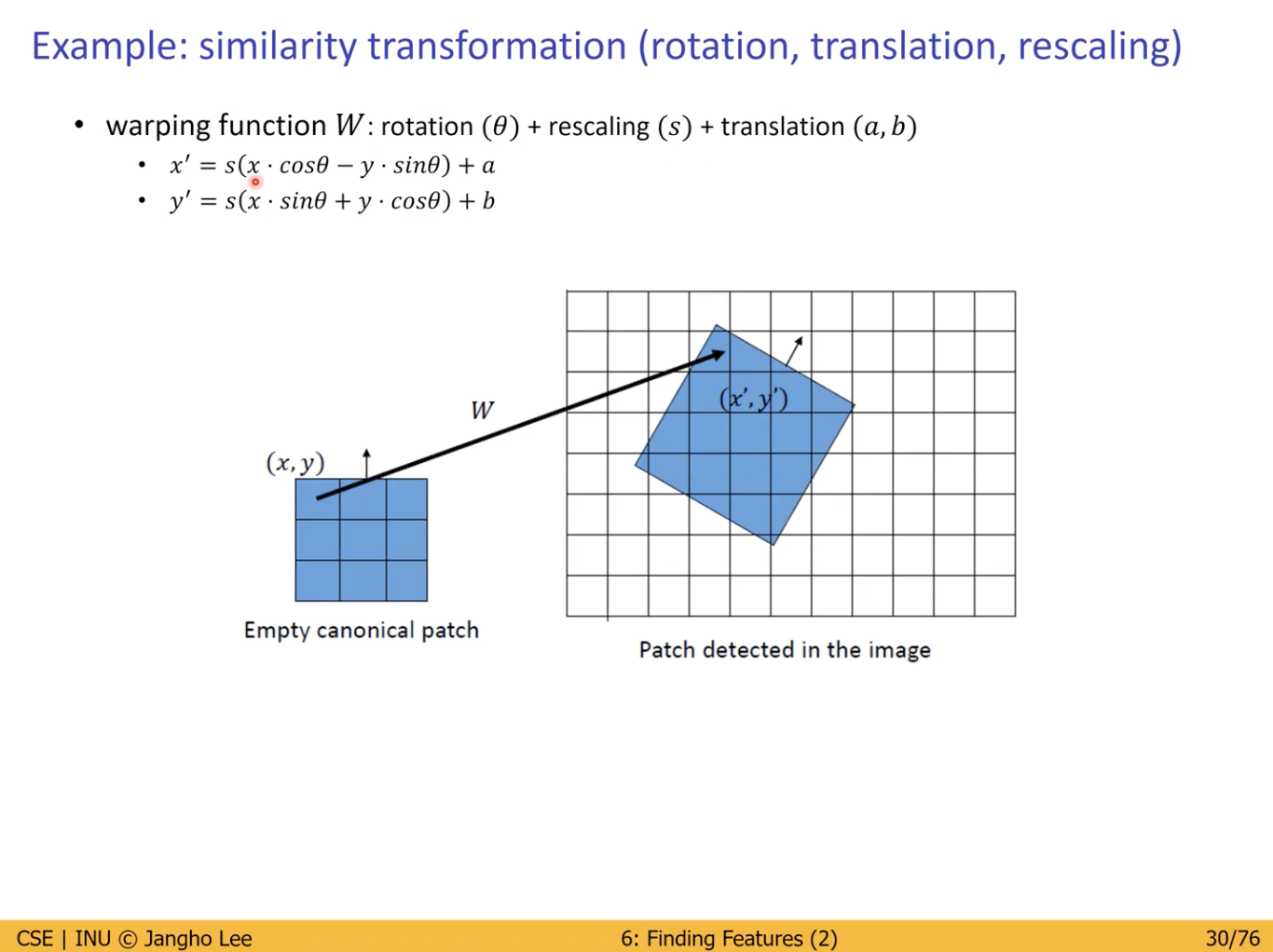
Warping Funtion은 Rotation, Rescaling, Translation 을 모두 포함하는 함수.

• Rotation : 이미지 회전
  
• Rescaling : 스케일링 (배율)
  
• Translation : 이미지 이동

Interpolation

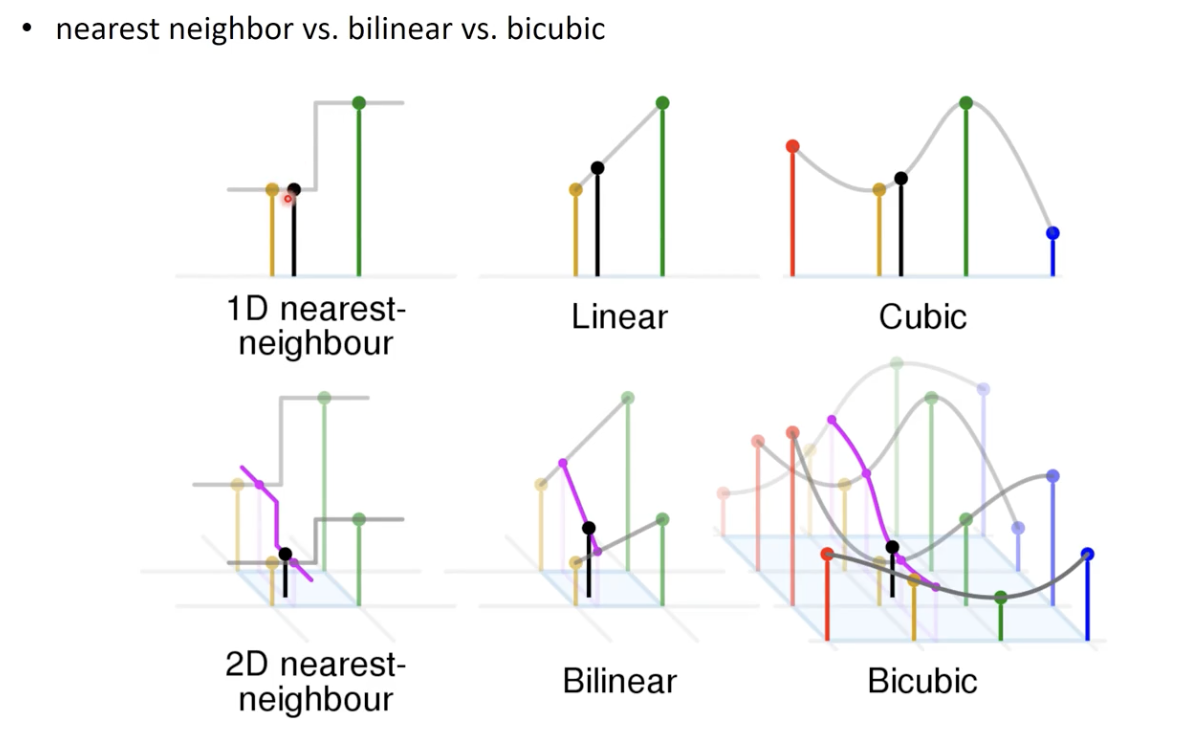
이미지를 Rescaling, Resizing, Warping 하는 것에 있어 많은 영향을 줌.

1. Nearest neighbor
   • 말 그대로 가장 가까운 값을 이용해서 다른 값을 “보관 / 할당”.
2. Bilinear
   • Linear : 좌표에서 직선을 생성, 그 직선에 대하여 각 점 간의 y좌표가 얼마나 대응되는지 Linear Function 을 이용하여 계산.
3. Cubic
   • 3차식을 이용한 Interpolation 기법
     
     

Blob Detector

Harris Detector

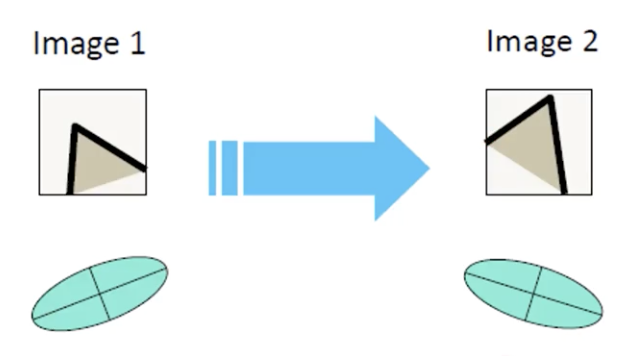
Rotation 에 Invariant 함.

• 주어진 이미지에 대하여 Rotation을 시키더라도 iden-value (이미지의 형태) 는 변하지 않는다.

Harris (Corner) Detector

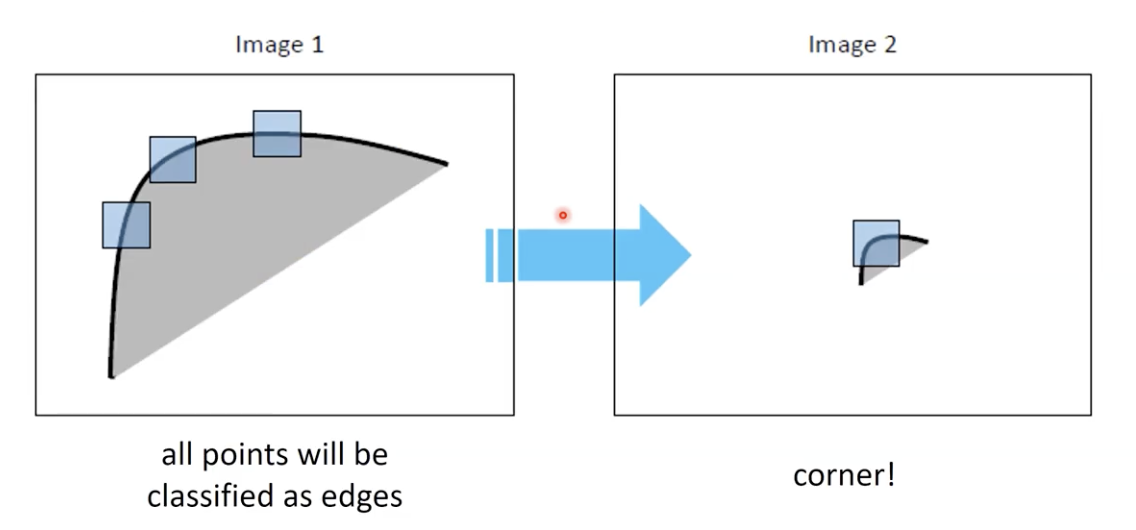
하지만 Harris Corner Detector 는 Image Scale 에 대해서는 Invariant 하지 않는다.

• 좌측 이미지는 확대된 코너 이미지.
  
  • Edge 로서 해석이 될 수 있다.
    
• 우측 이미지는 축소된 코너 이미지.
  
  • Corner 로서 해석이 될 수 있다.
    –> Corner 에 적용된 Harris Detector 는 Scale 에 대해서 Invariant 하지 않음.

Blob (Binary Large OBjects) Detection

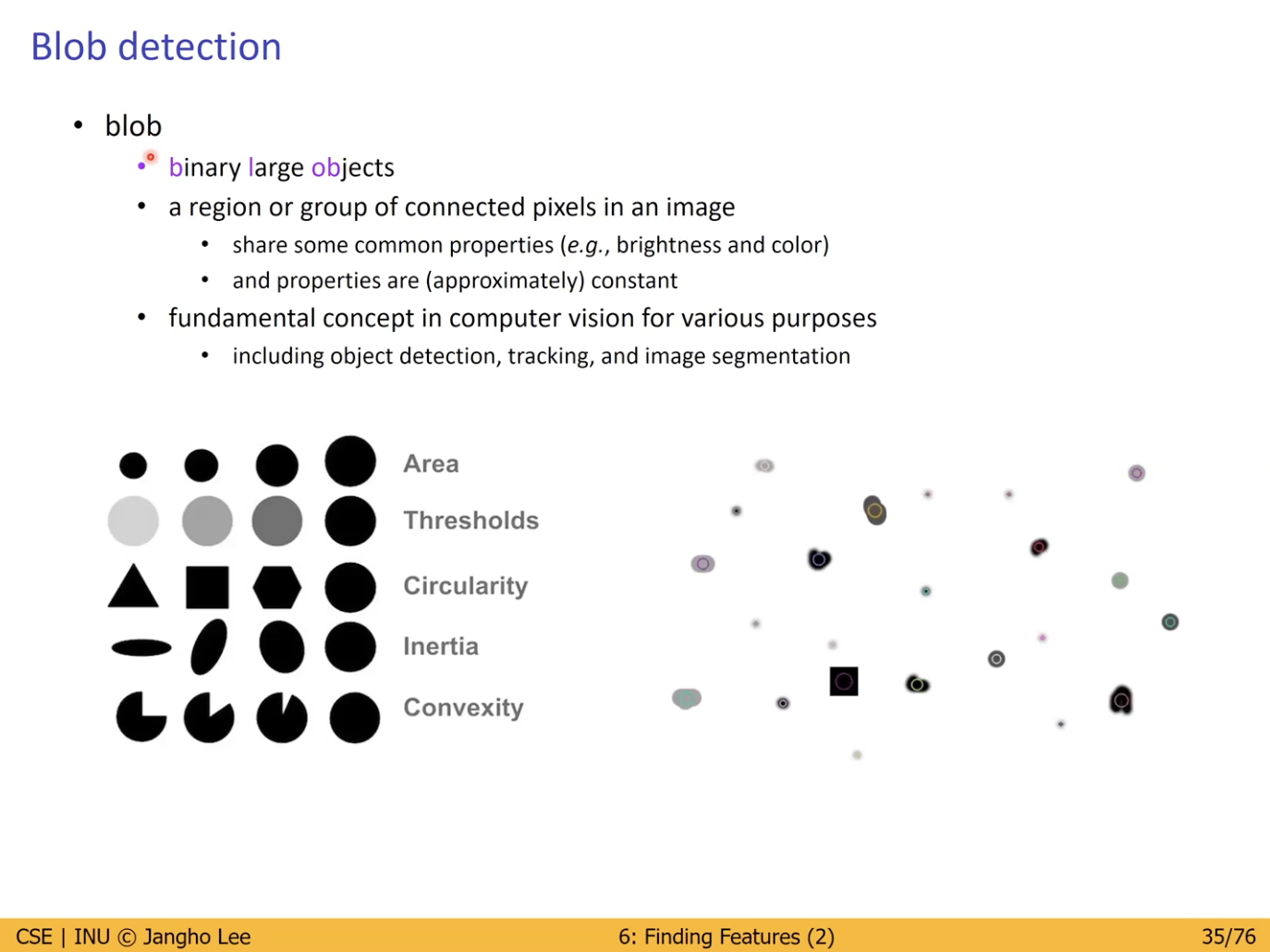
Image 내의 Pixel 들이 연결되어 있고 동시에 그룹(영역)을 가지고 있는 것.

• 비슷한 속성을 공유함. (색상, 밝기…)
  
  • 해당 속성은 일시적이지 않고 꾸준히 유지되는 속성이어야 함.
    
• 여러 형태의 모양이 포함됨.
  
• 컴퓨터 비전에서 가장 기본적인 Concept 로서 활용된다.

Blob Detection : Basic Idea

Image 에 대해 Blob Filter (Kernel) 을 Convolution.

• response 를 얻을 수 있게 됨.
  
  • 밝은 부분 : Maxima
    
  • 어두운 부분 : Minima
    
• Response 를 통해 Blob 영역을 찾을 수 있는 단서를 얻을 수 있다.

Blob Filter

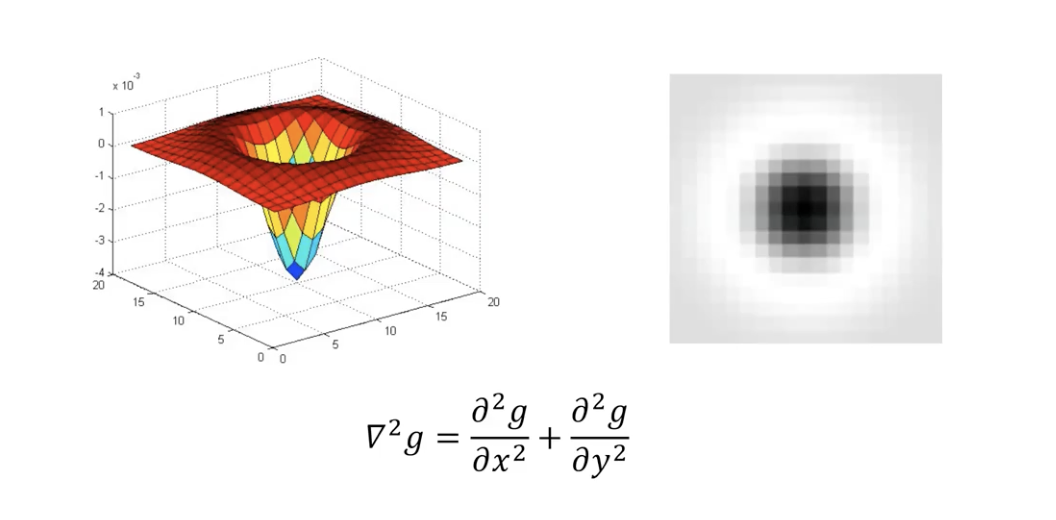
Blob Filter 는 일반적으로 Gaussian 을 두 번 미분한 Laplacian of Gaussian (LoG) 를 활용한다.

• LoG 는 Gaussian 의 속성을 따르기 때문에 원형을 띄고 있음.
  
• Gaussian 이기 때문에 Circularly & Symmetric 함.
  
  • Gaussian 함수가 중심을 기준으로 원형 대칭을 가지고 있다는 의미.
    
    • Gaussian 함수의 값은 중심에서 최대가 되고 중심에서 멀어질수록 감소하는 형태로 분포.
      
    • Gaussian 함수는 회전에 대해서 대칭.
      
      • 즉 어떤 각도로 회전하더라도 모양이 변하지 않음.
        
      • 이러한 원형 대칭성과 회전 대칭성은 이미지 처리에서 필터링 작업을 수행할 때 유용.
        
      • 영상의 특정 방향 또는 회전에 민감하지 않도록 도와줌.

Edge Detection with LoG

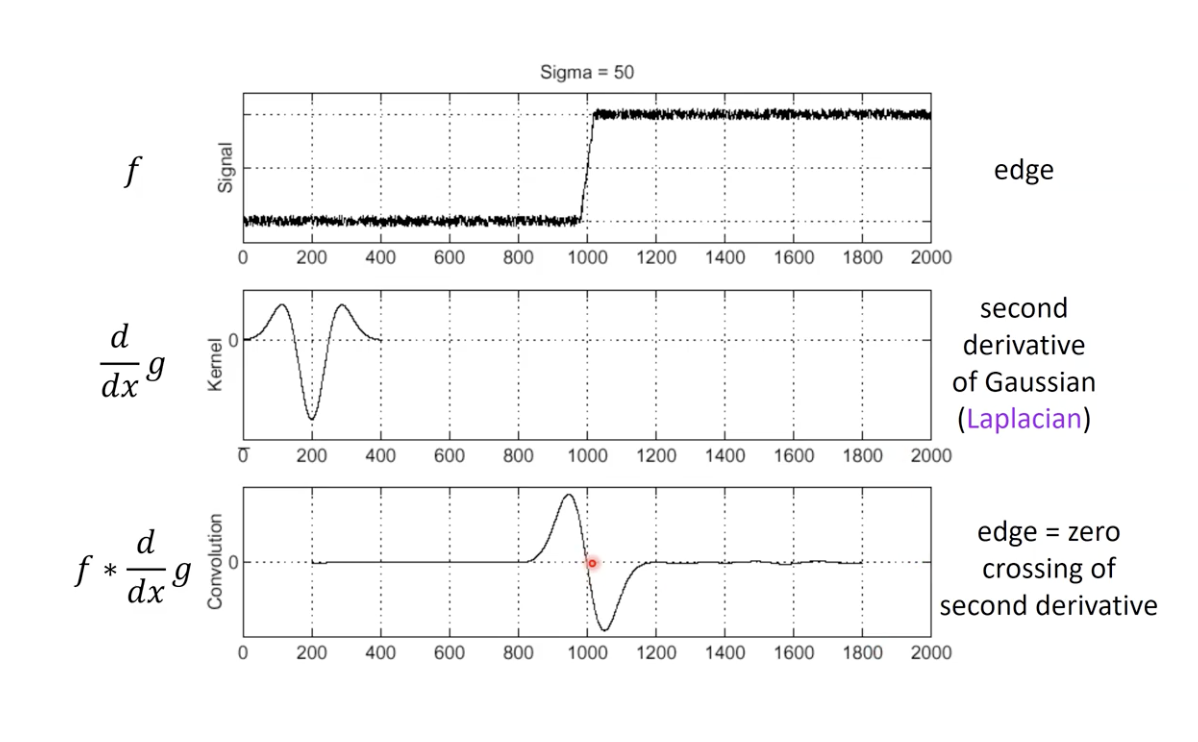
Convolution 결과 그래프에서 0을 거치는 순간의 점 근방이 Edge 라고 판단 가능.

Original Signal 그래프의 Edge 부분을 나타내는 0 과 1 사이 변환 구간 == Edge

• LoG Filter 를 적용 했을 때 0 을 거치는 순간과 같음.
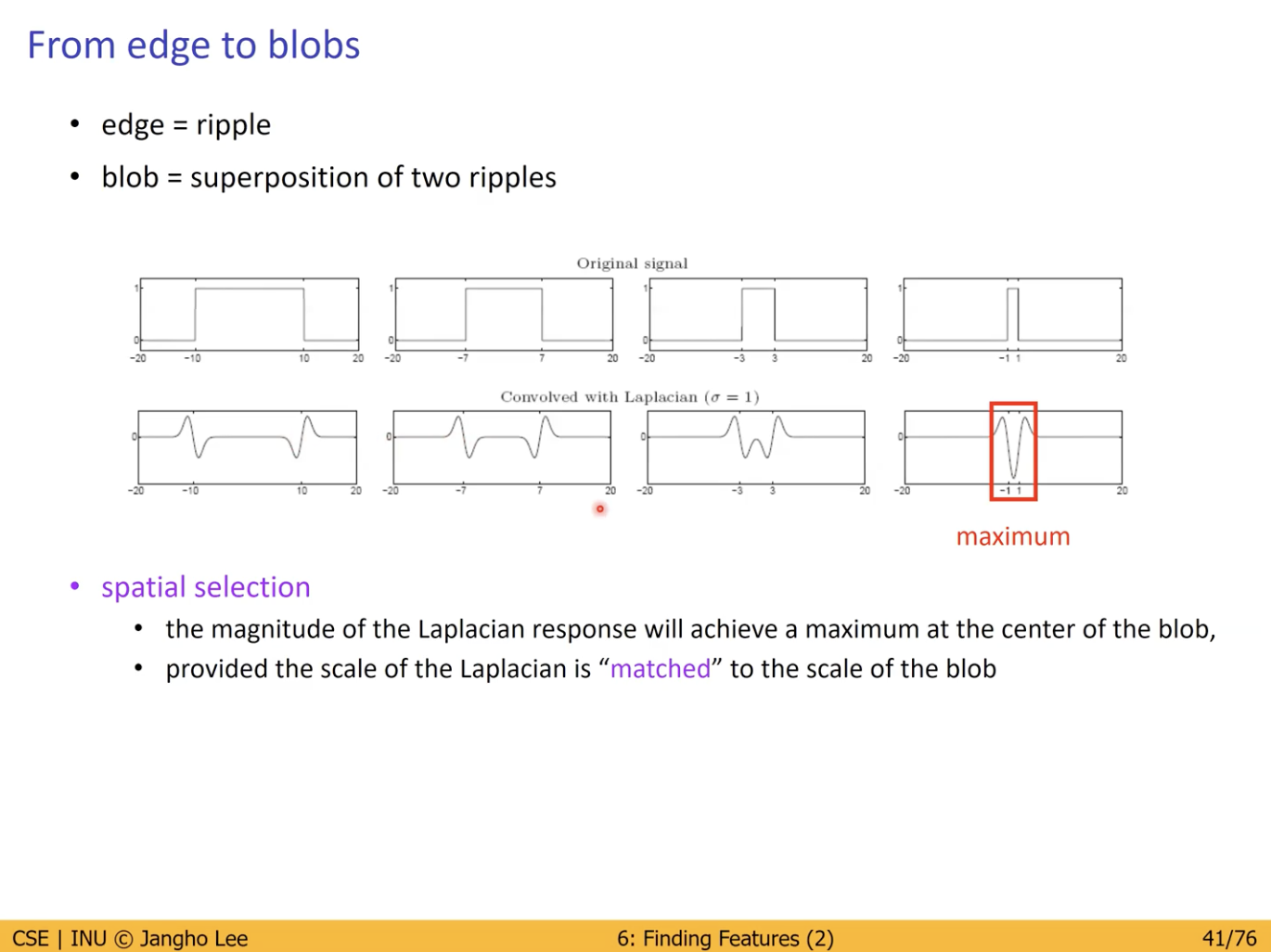
• 두 Edge 사이 값이 변하지 않고 일정.
  • 두 Edge 사이 구간은 Blob 이라고 볼 수 있음.

LoG 를 적용 (Convolution) 했을 때, Maximum & Minimum 이 발생하는 구간이 Blob 이다.
적절한 시그마를 찾는 것이 Blob 을 찾는 것에 있어 가장 중요함.

Scale Selection

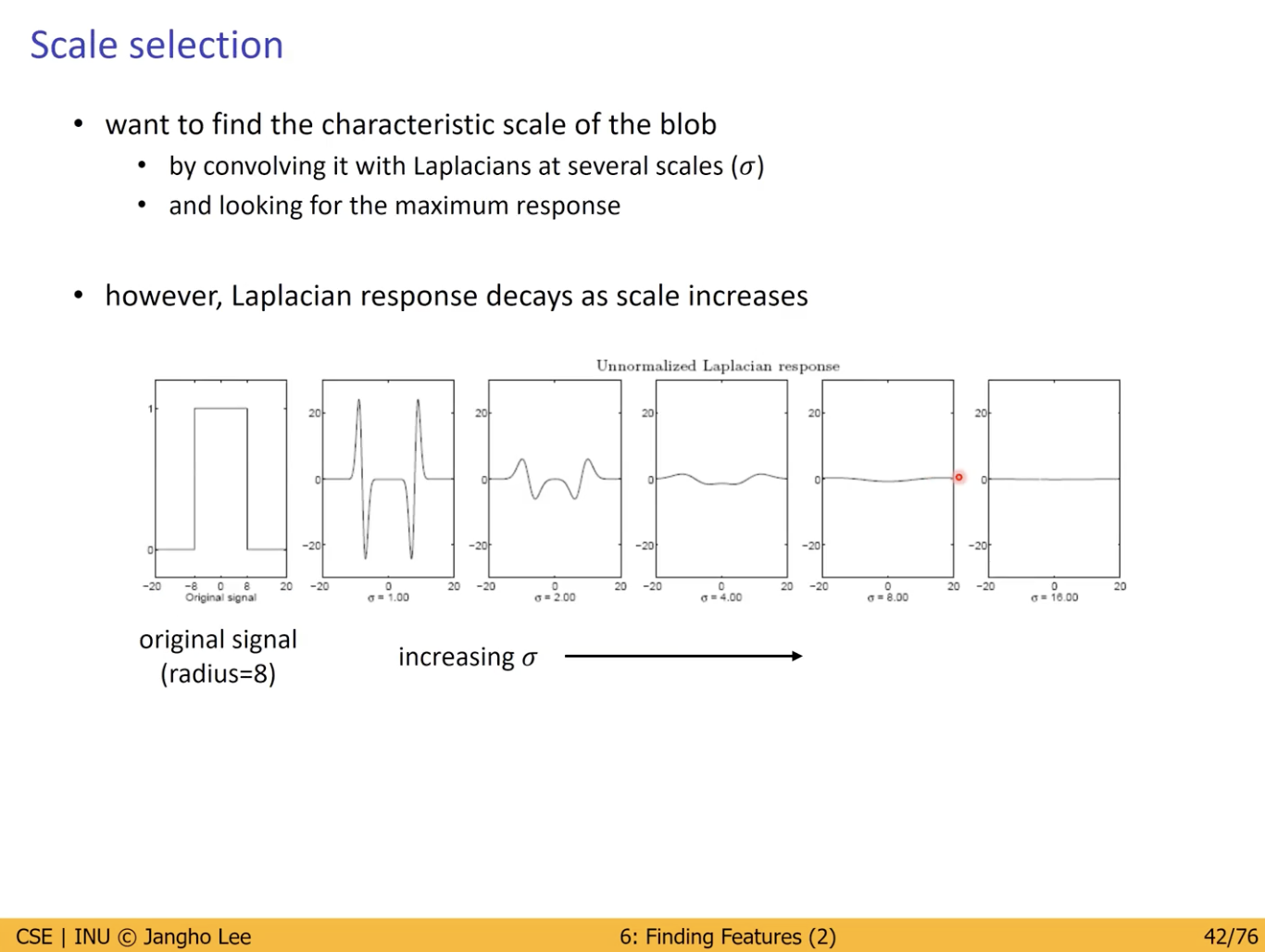
Blob 의 특정 Scale 찾기.

• LoG 를 사용해서 (Convolving) Maximum Response 를 찾을 것.
  문제점
  
• Laplacian 에 대한 Response 는 Scale 이 커질수록 Response 가 작아짐.
  
  • 위 사진과 같이 Original signal 에 대해서 시그마 값이 커질수록 Laplacian Response (Kernel 에 대한 Response) 가 작아지는 것을 볼 수 있음.
    
  • 이는 Maximum Response 를 찾기 어려워짐.

Scale Normalization

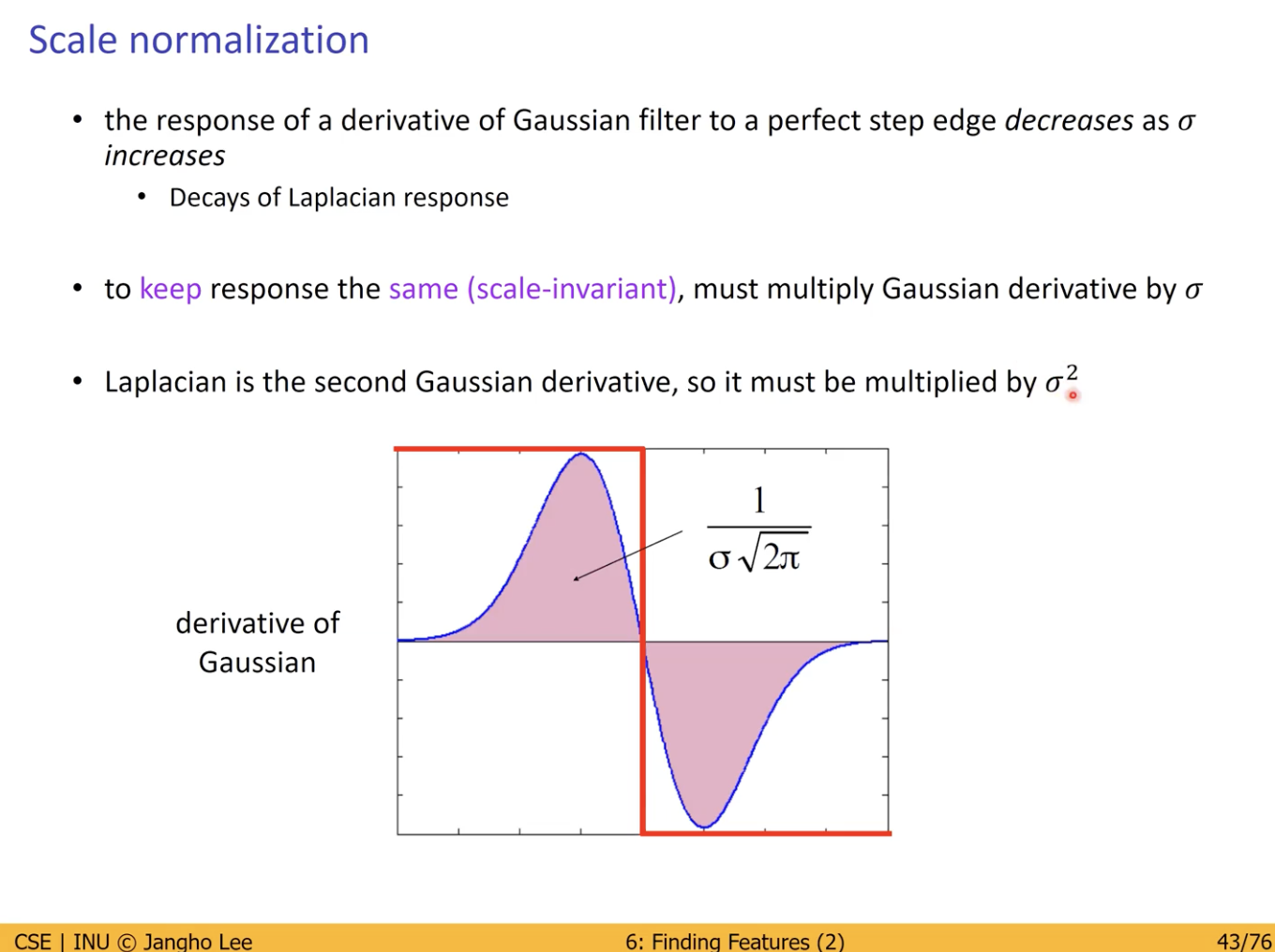
Scale Selection 의 문제점 해결을 위해 나온 기법.

LoG 의 시그마 값이 커질수록 Response 가 작아지는 문제.

이에 Response 를 유지하기 위해 Gaussian 에 시그마(Factor) 를 곱해 사용.

• LoG 는 Gaussian 을 두 번 미분한 것이기 때문에 시그마의 제곱을 곱해 활용.

Effect of scale normalization

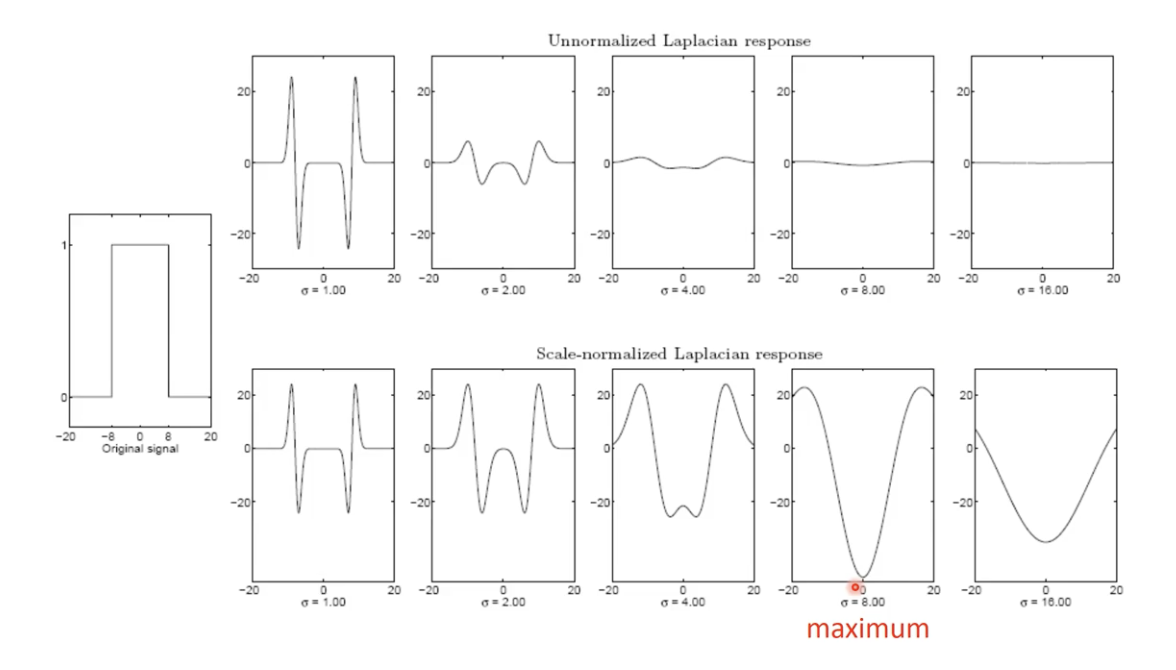
• 상단 그래프는 Scale normalization 적용 전.
  
• 하단 그래프는 Scale normalization 적용 후.
  

• Scale Normalization 을 통해 우리는 Blob에 적합한 Scale 의 크기를 찾아 낼 수 있다.

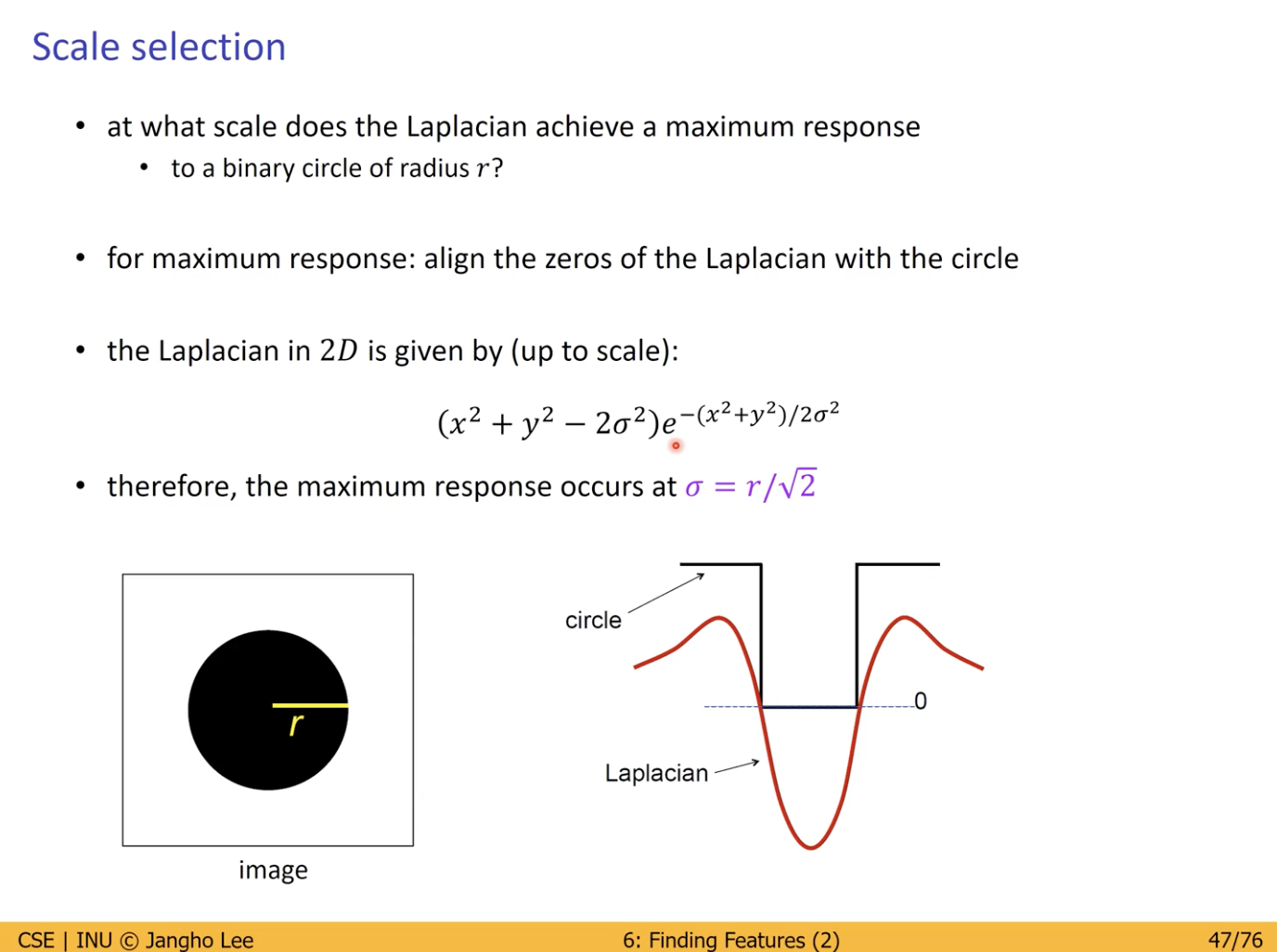
Scale Selection 문제 해결

• 반지름이 r인 Blob에 대하여 Laplacian 이 가장 좋은 Maximum Response 를 나타내는 Scale의 크기는?
  • Sigma = r / √2

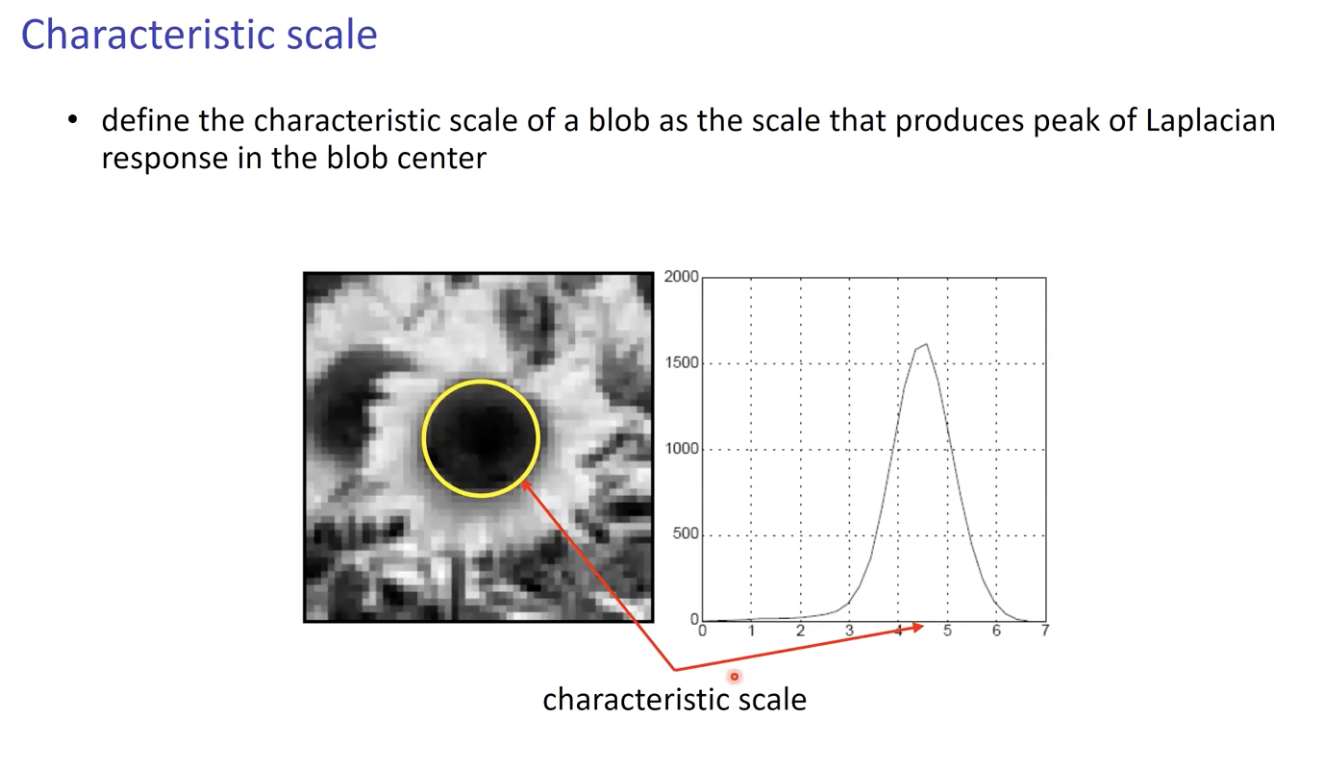
• Blob 의 Center 에서 가장 Peak 한 Laplacian Response 를 생성하는 Scale 을 Characteristic Scale 이라고 한다.

SIFT Blob Detector and Descriptor

Scale 에 Invariant 한 Feature Transform.

General Idea

• Image 의 특징을 찾아내는 것.
  
  *SIFT Blob Detector 의 특징**
• Translation Invariant
  • 대부분의 Feature Extractor 들이 가지고 있는 속성.
• Rotation Invariant
  • Harris Corner Detector 와 같은 속성.
• Scaling Invariant
  • Harris Corner Detector 의 단점을 해결.
    • 코너 / 엣지 구분 가능.

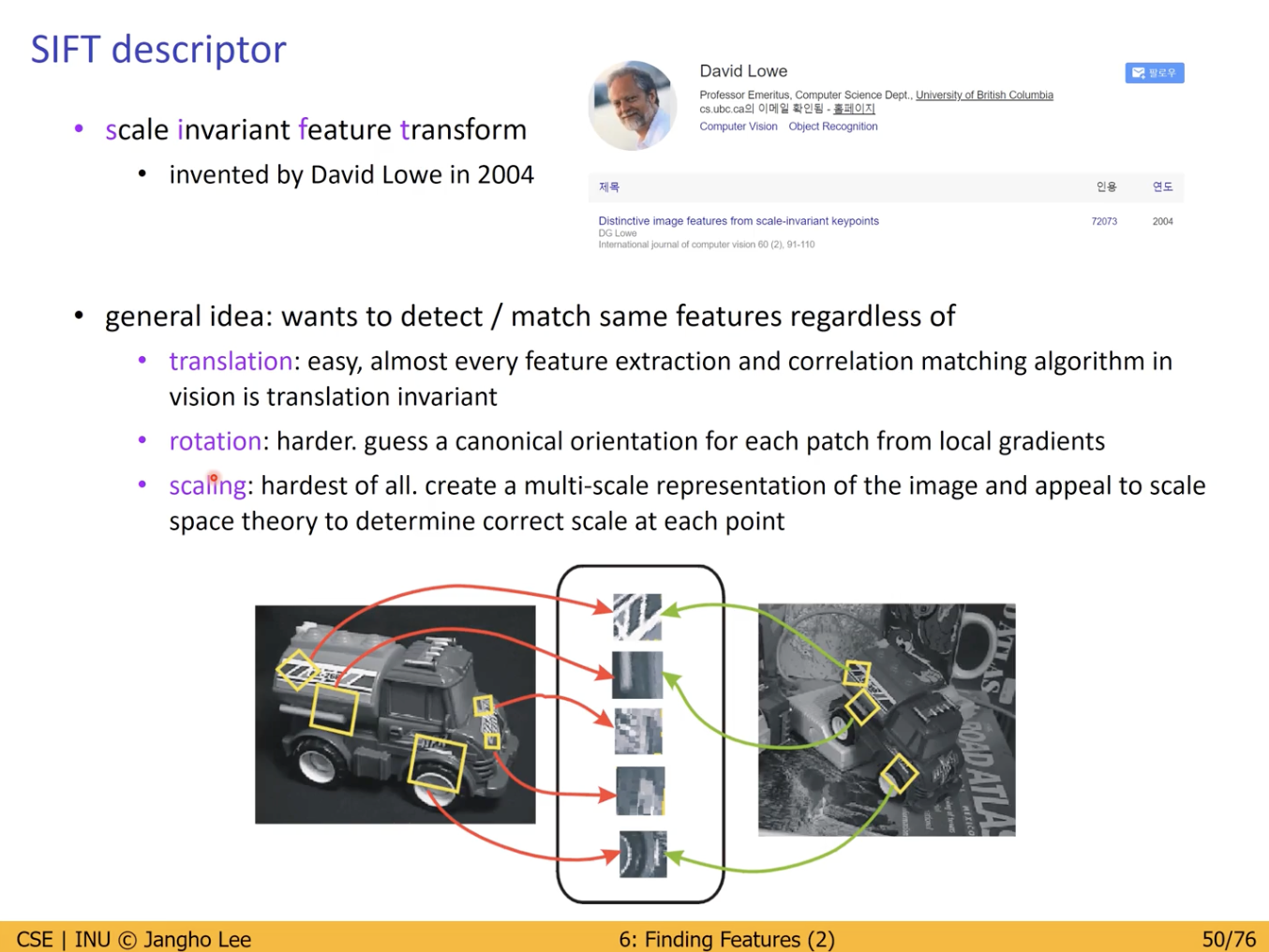
위 사진처럼 각 이미지의 특징적인 Patch 가 회전이 되거나 Scale 되어 Patch 의 크기가 축소 및 확장되어도 잘 찾아내는 것을 볼 수 있다.

SIFT 의 주요 계산 과정

1. Scale-space Extrema Detection
   • Scale-space 에서 극값을 찾아내는 과정.
   • Laplacian Pyramid (Difference of Gaussian)
     • 모든 Scale 에서 극값들을 찾아냄.
2. Keypoint Localization & Filtering
   • 이미지내에서 특정 영역 - Keypoint candidate, 즉 후보군들을 찾아냄.
   • 그 과정에서 불필요한 영역 (Keypoint) 들을 제거.
3. Orientation Assignment
   • 해당 Keypoint 가 어떤 Orientation 을 가지고 있는지.
     • 해당 이미지를 어떤 특징으로 만들기 위해 어떠한 Gradient 방향을 가지고 있는지 찾아내는 과정.
4. Creation of SIFT Keypoint Descriptor
   • 이미지를 Matching 시키기 위해서는 직접 비교가 아닌, Vector 로 바꾸어 비교를 수행하게 됨.
   • 해당 과정을 진행하기 위해 주어진 이미지에서 특정한 속성들을 추출하여 수치화 시키는 과정.

Step 1. Scale-space Extrema Detection

앞서 LoG 에서 확인했듯이, 이미지 블록들을 찾기 위해 Charateristic Scale 을 확인했었음.

어떻게 Scale-space 를 확인하는가?

• 원본 이미지에서 점진적으로 Blurr 한 이미지를 만들어 낸다.
  • 이미지에 대하여 Gaussian Filter 를 적용하여 수행.
• 이때 L 로서 표현되는 Scale-space 를 정의 할 수 있다.
  • L(x, y, σ) = G(x, y, σ) * I(x, y)
    • L = Image 에 Gaussian 을 Convolution.
    • σ = Scale Parameter (Kernel Size)
      • σ 가 증가 할수록, Image는 점점 더 Blurr 해짐.
• Difference of Gaussian
  • 해당 Image 에 Gaussian Kernel 을 적용한 결과 간의 차이

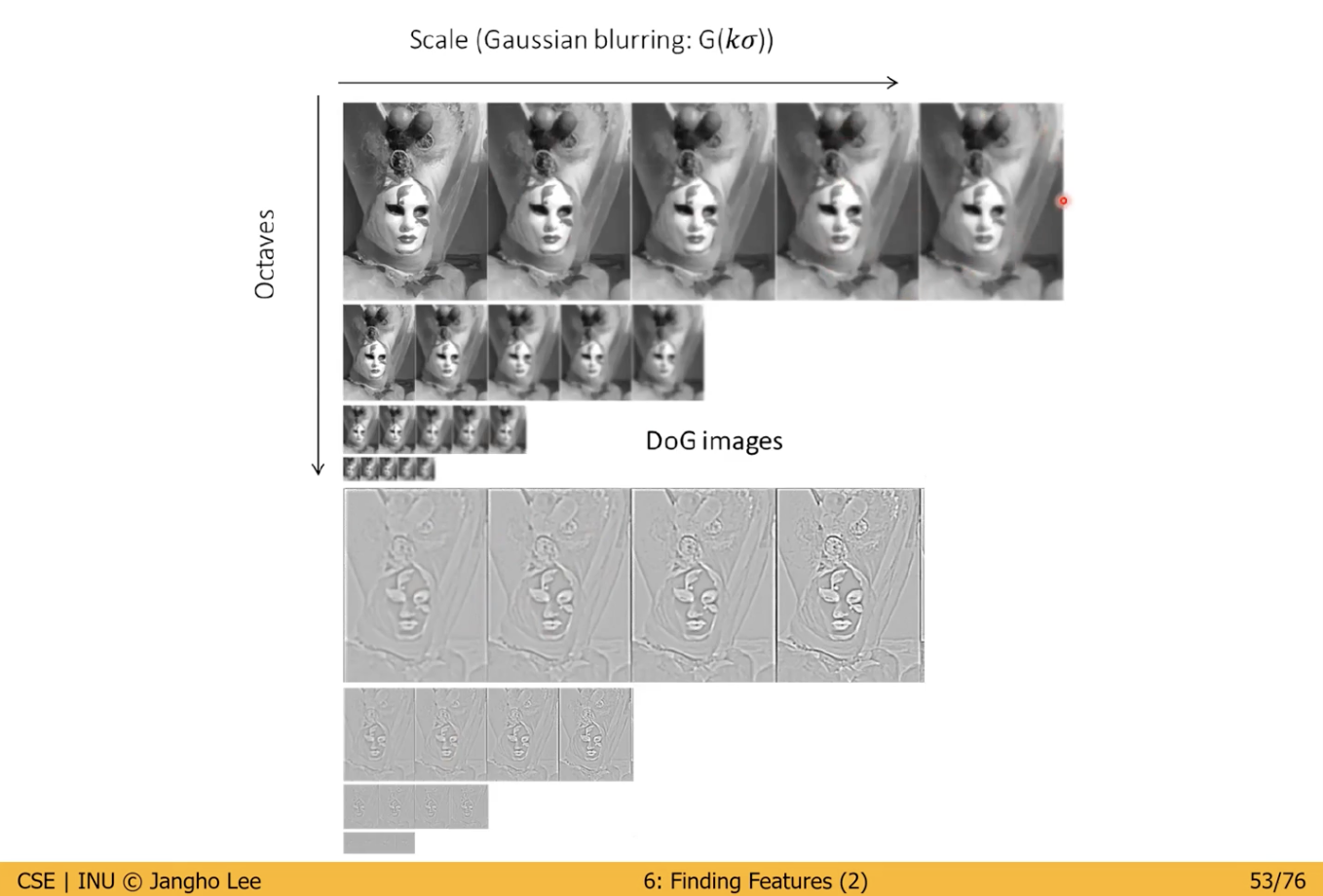
1. Scaling 에 따른 Blurring 의 효과 및 이미지의 축소 / 확대에 따른 변화
2. 좌우 인접한 사진 간의 차이를 나타내는 DoG (Difference of Gaussian)

DoG (Difference of Gaussian) vs LoG (Laplacian of Gaussian)

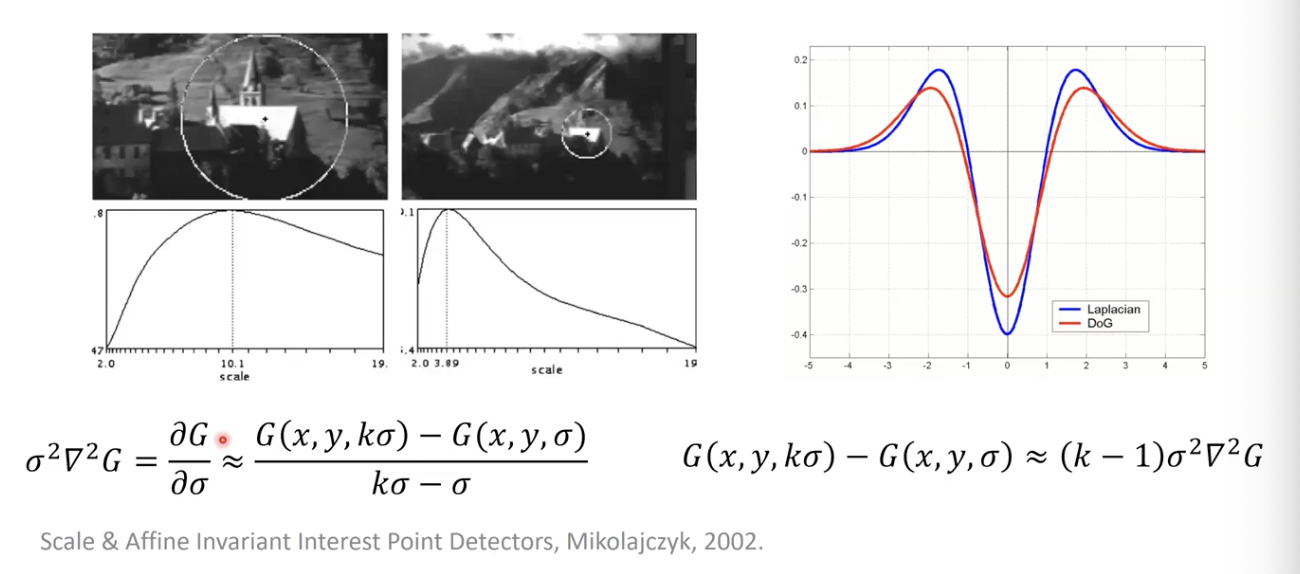
Laplacian of Gaussian (LoG) 는 계산하는 것에 있어 적지 않은 시간이 소요됨.

• 대신 Difference of Gaussian (DoG) 을 통해 Laplacian 과 근사한 값을 도출 해낼 수 있음. (Scale & Affine Invariant Interest Point Detectors, Mikolajczyk, 2002.)

Difference of Gaussian (= Laplacian Pyramid)

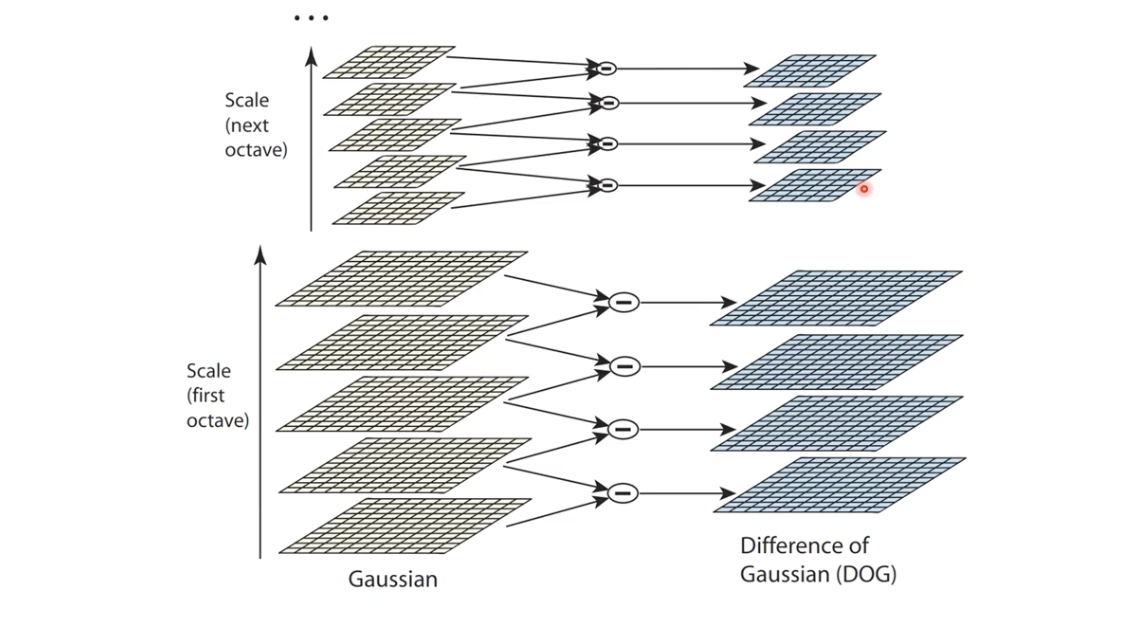
쉽게 말해서 Scale 이 비슷한 Image 간의 차이를 도출해내는 과정.

• 비슷한 Scale 을 가진 Image 간의 차이 == DoG == 이미지의 극값
• 위 사진 우측의 DoG 는 결국 이전에 본 아래 사진과 같다.

Step 2. Keypoint Localization & Filtering

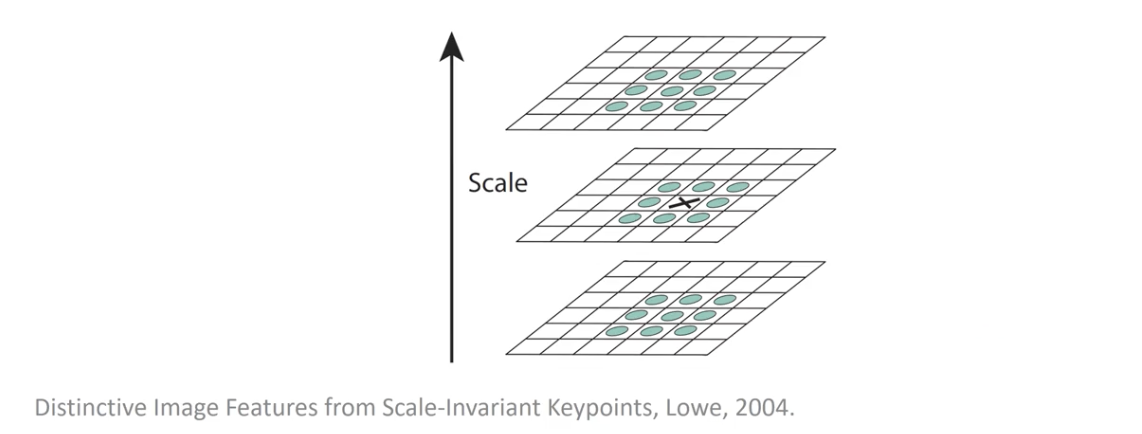
이전에 계산한 DoG 의 윗층과 아랫층을 고려.

• 가운데 층에 존재하는 특정 픽셀의 인접한 Neighbor 에 대하여 값을 계산.
  • 윗 층에 9개 Neighbor
  • 자신의 층에 자신을 제외한 8개 Neighbor
  • 아랫층에 9개 Neighbor
    • 총 26 Neighbors 에 대하여 비교를 수행.
• 위 과정에서 Local Extrema (Maximum or Minimum) 추출 가능.
  • 위 값을 추출 후 SIFT Keypoint 의 Candidate 로 가지고 있게 된다.

위 과정에서 추출되어 가지고 있는 Keypoint Candidates 들은 보라색 점으로 나타난 상태.

• Matching 하고자 하는 Corner 와 Edge 도 잘 추출하고 있지만, 하늘과 같은 이미지의 Pixel 변화가 많이 없는 부분도 많이 Detect 하고 있음
• 이러한 부분을 정제하는 과정이 필요.

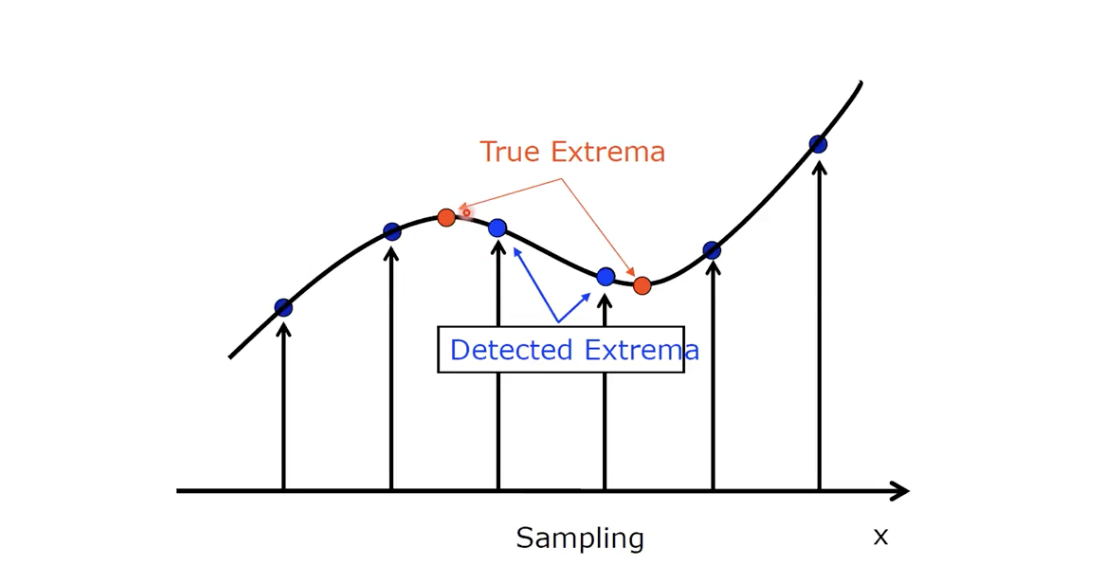
빨간색 점이 실제로 우리가 원하는 Local Extrema (Maximum, Minimum).

• 하지만 현재 Detect 되고 있는 보라색 점들은 파란색 점.
• 진짜 극값을 찾고 있지 못하는 문제.

이 문제점의 해결을 위해 위와 같은 과정을 거쳐 Keypoint Localization 의 성능을 향상.

• 기존에 찾은 Keypoints 들의 Contrast 가 특정 수치 (예: 0.03) 보다 작은 경우 (Weak Extrema), 해당 Keypoint 는 Candidate 에서 제거함.
• 그 결과로, 이전에 파란색 점으로 나타난 진짜 극값이 아닌 Keypoint 들은 제거됨.

이후, 기존에 Candidate 로서 존재하던 가짜 극값 Candidates 들은 모두 제거가 된다.

추가적인 후처리 과정

• Corner 근처에서는 Gradient 가 두 가지 이상의 방향을 가지는 경우가 존재 할 수 있음.
• Corner 및 Edge 부근에 존재하는 Keypoints 들을 더욱 세밀하게 정제 가능.

Step 3. Orientation Assignment

이전 Step 까지 찾은 Keypoints 들의 Orientation 을 찾아주는 과정이 필요.

• 우리는 Rotation & Scale 에 대하여 Invariant 한 keypoints 들을 찾아야 함.

과정

• 좌, 우측 이미지에 대하여 Descriptor 를 추출.
  • 특정한 Vector 의 형태로 값이 도출됨.
  • 그것이 Rotation 과 Scale 에 대한 정보를 포함하도록 특징을 추출해야함.
    • 이를 위해 Gradient 의 Orientation 과 Magnitude 를 계산.

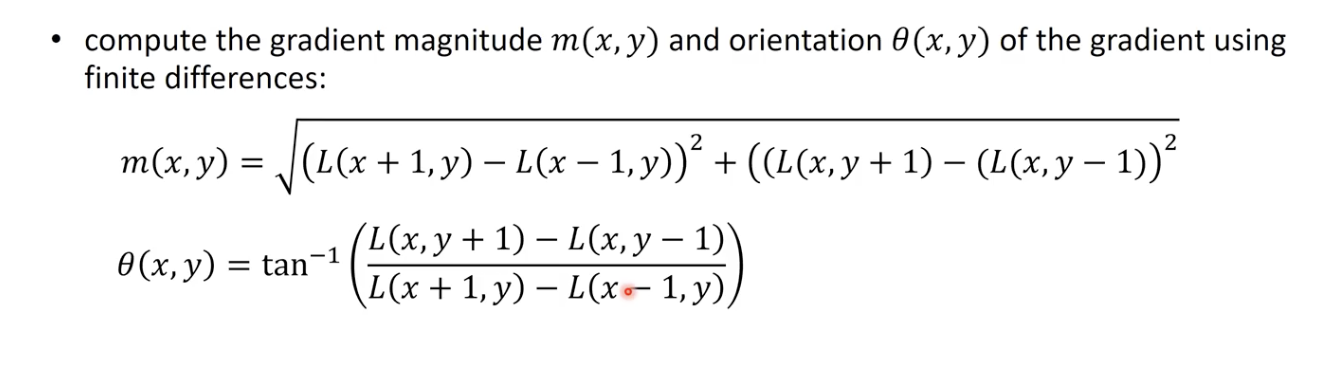
Magnitude

• 일반적으로 두 개의 픽셀의 차를 이용하는 과정으로 이루어짐.
  • (x+1) - (x-1) , (y+1) - (y-1)
• x, y 전체의 Magnitude 계산.
  • x 및 y 방향의 Magnitude 계산 후 그것들의 √제곱의 합

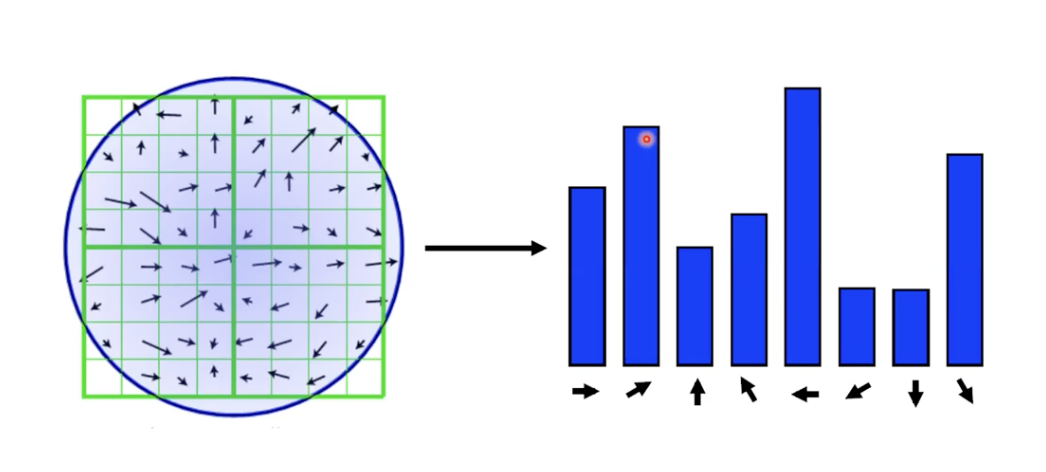
이후 각각의 Orientation 에 대하여 Histogram of Local Gradient (HoG Descriptor) 를 구한다.

• 어느 방향으로부터 유래했는지를 계산해놓는다.

Step 4. Creation of SIFT Keypoint Descriptor

현재까지 우리가 가지고 있는 것

1. 이미지에 대한 좌표
   • x, y
2. Scale 정보
   • σ
3. Magnitude
   • m
4. Orientation
   • 𝜃

위 정보를 이용해서 우리는 새로운 Local Image Descriptor 를 만들어냄.

• 해당 Local Image Descriptor 는 Illumination 과 Viewpoint 에 대하여 Invariant 함.
  • Viewpoint
    • 최대 50도 정도의 변화에도 동일한 특징을 잘 탐지.
  • Illumination
    • 큰 변화에도 특징을 잘 탐지하는 것이 알려져 있음.

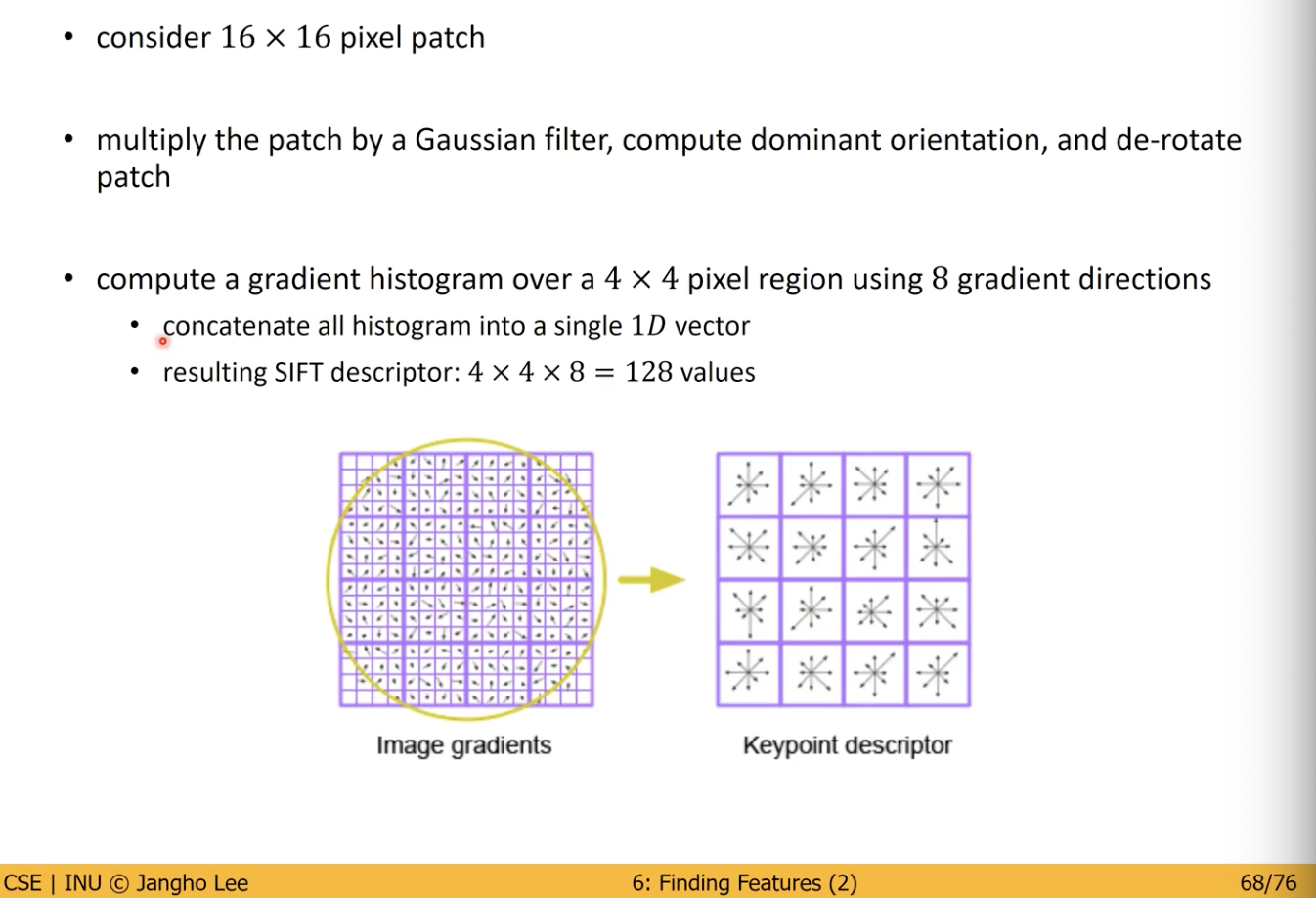
SIFT Keypoint Descriptor 를 만드는 과정

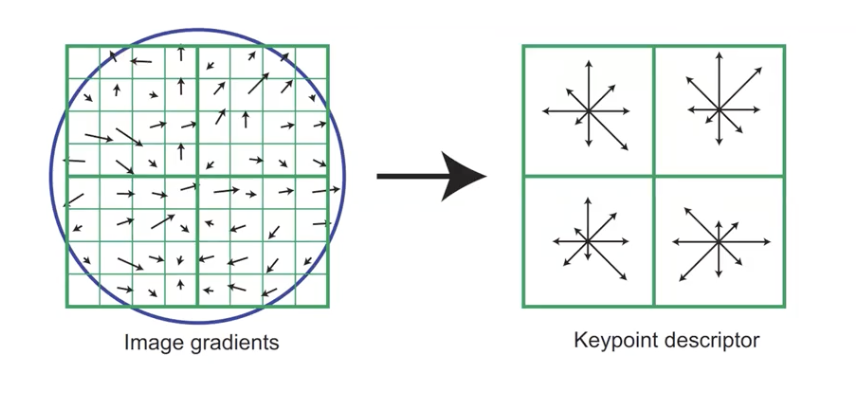
1. Compute a gradient histogram over a 4 X 4 pixel region using 8 gradient directions
   • 4 X 4 Pixel 의 영역에 대하여 8가지방향에 대한 성분들을 고려.
2. Compute a weighted histogram of 4 X 4 windows
3. Gaussian weighting around center (σ = 0.5 time that of the scale of a keypoint)
4. 4 X 4 X 8 = 128 dimensional feature vector
   • 우리가 고려하는 Pixel 영역의 크기와 전체 방향을 고려하여 총 128 차원의 특징들을 추출해내게 된다.

지식 공유 및 기록을 위한 컴퓨터 비전 개인 학습 포스트입니다. 피드백은 항상 환영합니다! 긴 글 읽어주셔서 감사합니다.

처음으로~

Task Lists

• Invariant Descriptors
• Scale
• Rotation
• View Point
• Blob Detector
• Harris Detector
• Blob (Binary Large OBjects) Detection
• Scale Selection
• Scale Normalization
• Scale Selection 문제 해결
• SIFT Blob Detector and Descriptor
• SIFT 의 주요 계산 과정
• Step 1. Scale-space Extrema Detection
• DoG (Difference of Gaussian) vs LoG (Laplacian of Gaussian)
• Difference of Gaussian (= Laplacian Pyramid)
• Step 2. Keypoint Localization & Filtering
• Step 3. Orientation Assignment
• Step 4. Creation of SIFT Keypoint Descriptor
• SIFT Keypoint Descriptor 를 만드는 과정