Artificial Neural Networks - Multilayer Perceptron(MLP), Softmax Function, Forward / Backward Propagation, Error measures

---

Artificial neural networks (ANNs)

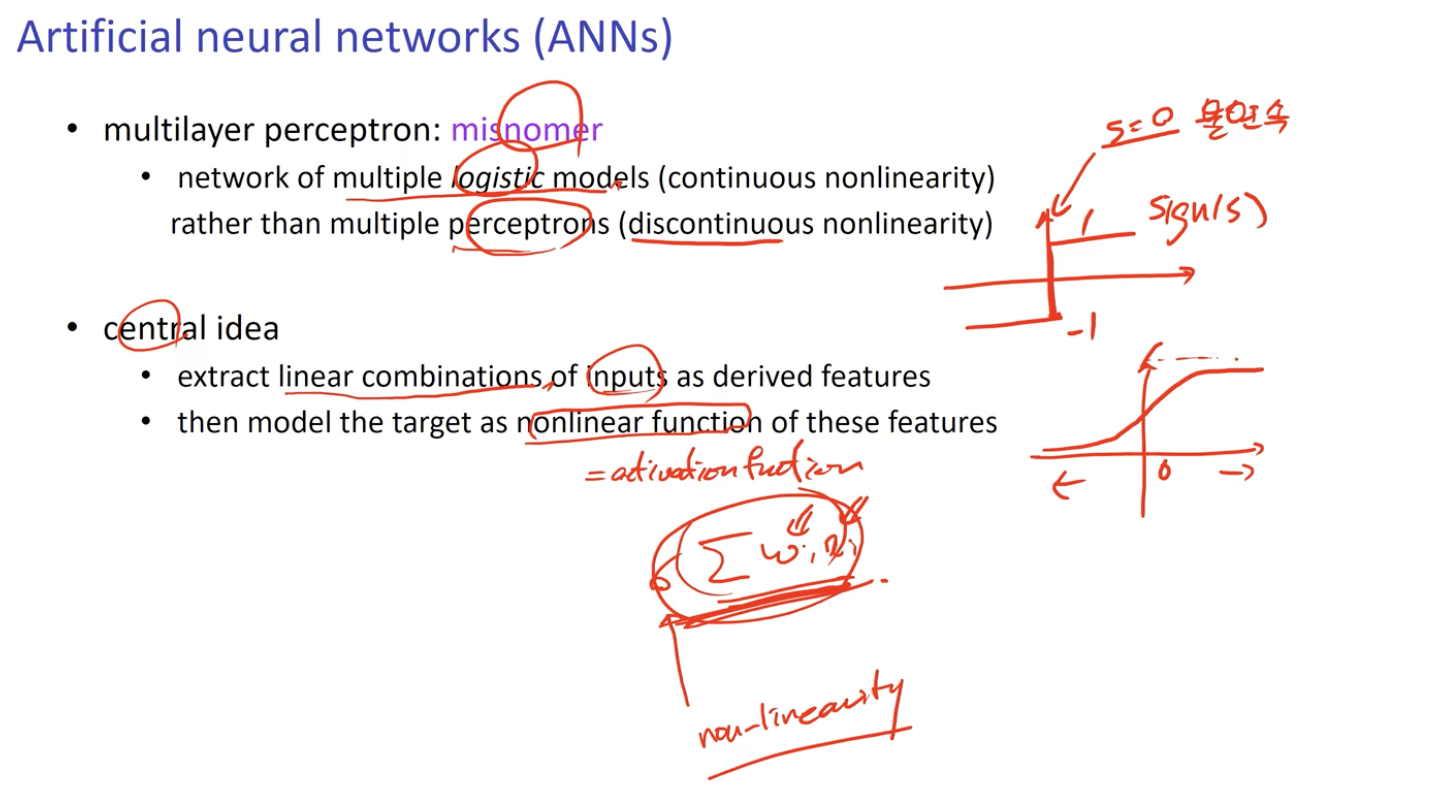
Multilayer perceptron : misnomer

• network of multiple logistic models (continous nonlinearity)
• Perceptron은 불연속성이지만 misnomer 은 연속적인 특성을 가짐.

메인 아이디어

• 추출된 input 에 대한 선형 조합에서 정보를 추출.
• 그것에 대하여 Activation Function 을 취함.

Models of a Neuron

1. Synapses
   • weights 로서 구현
2. Adder
   • sumation.
   • input vector -> scalar
3. Activation function (Possibly Nonlinear)

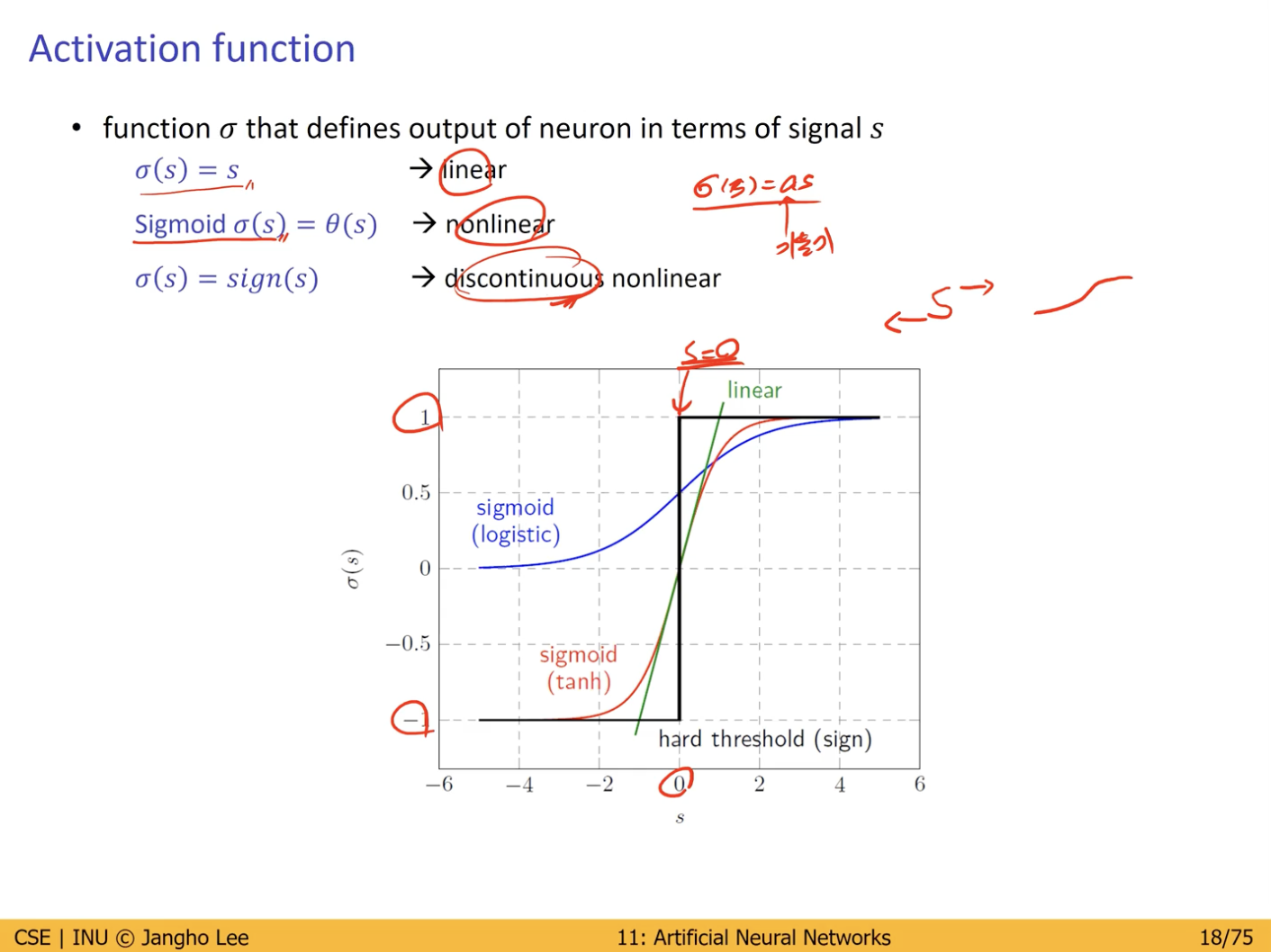
Activation function

ReLU (중요)

가장 많이 쓰이는 Linear Unit.

• 장점
  • back-propagation 수행 성능 좋음.
  • 추후 Vanishing gradient 문제 해결 가능
    • Vanishing gradient: Layer 가 점점 깊어지면서 gradient 가 흐릿해짐.
• 한계
  • 프로그램이 죽을 수 있음.
    • Leaky ReLU 를 사용하여 극복 가능.

Multilayer Perceptron

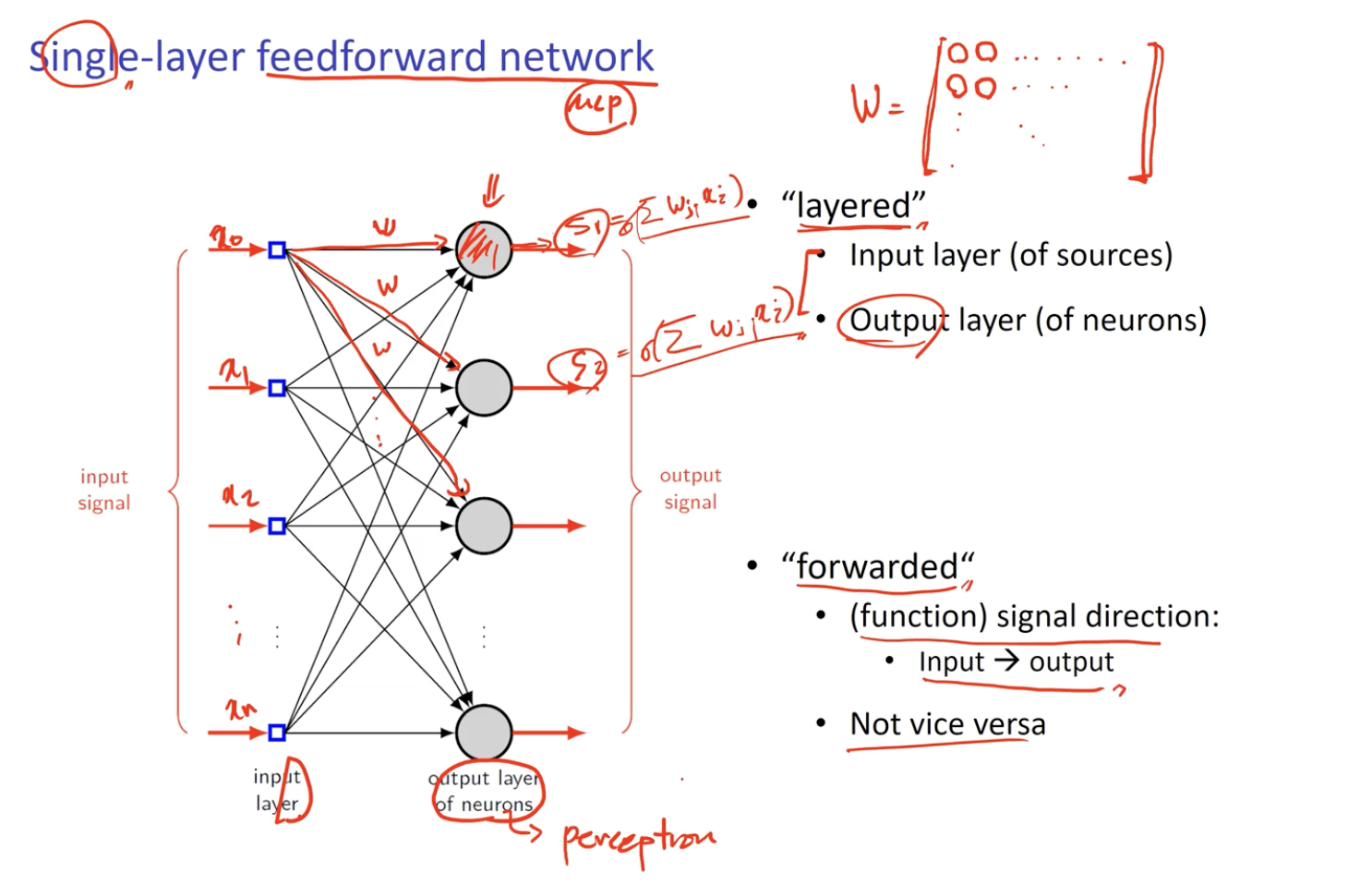
Single-layer feedforward network

파란색 박스 : Input
회색 원 : neuron (= perceptron)

• 둘 사이에 연결이 존재한다 == 둘 사이에 weight 가 존재한다.

각 입력과 Perceptron 사이의 가중치(weight) 를 Matrix 형태로서 나타낼 수 있음.

• Input layer (입력 Layer)
• Output layer (Perceptron Layer)

Forwarded

• 모든 Signal 은입력에서 Output(Perceptron) 방향으로만 진행.
• 반대 방향으로는 불가.

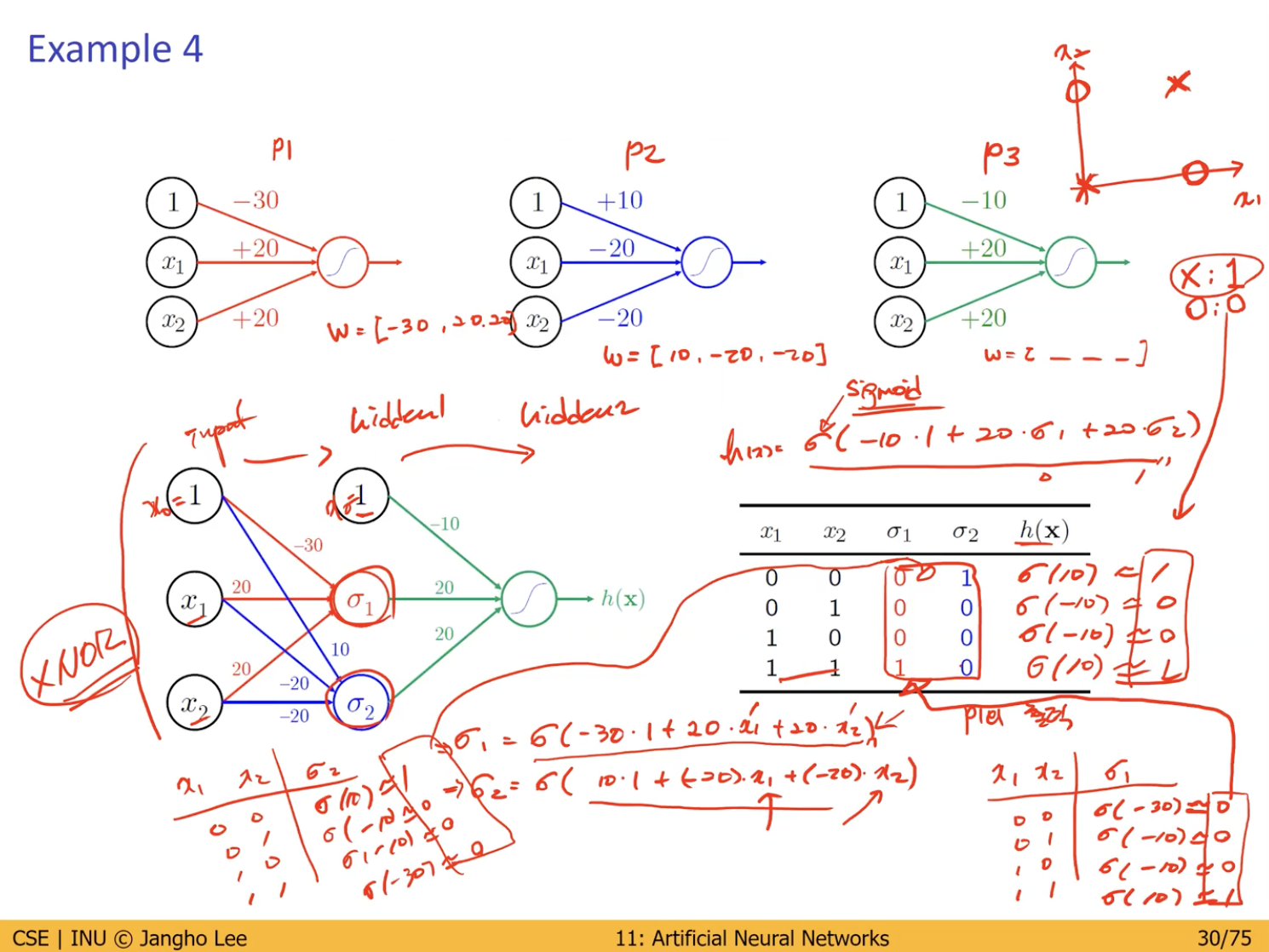
Multilayer feedforward network (Multilayer Perceptron)

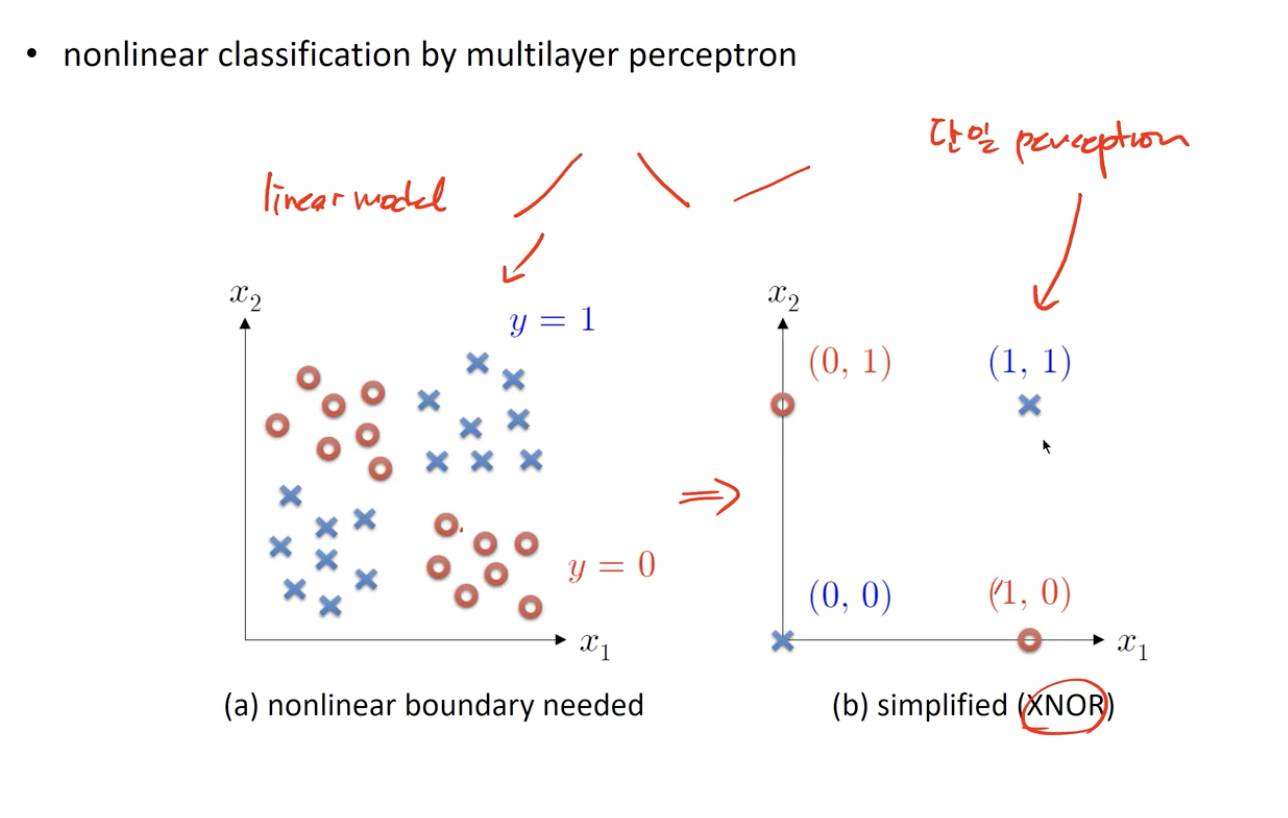
탄생 배경

• XNOR 과 같은 분포는 선형 모델로서 정확한 클래스 분류가 불가능 했음.
• 이에 Layer (Perceptron) 를 여러 개 쌓아 올림으로서 Multilayer 를 만들어 Nonlinear 문제를 해결.

Input layer 와 Output layer 사이에 여러 개의 hidden layer 가 존재함.

• 각 Layer 의 Output 이 다음 Layer 의 Input 이 되어 Foward 방향으로 진행.

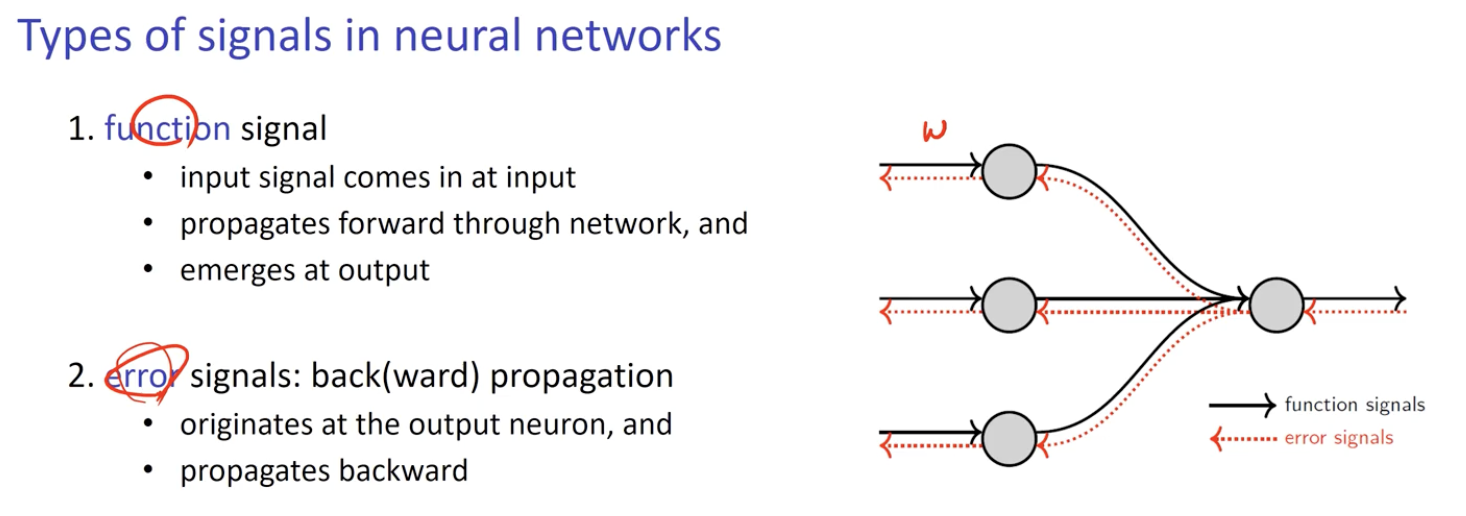
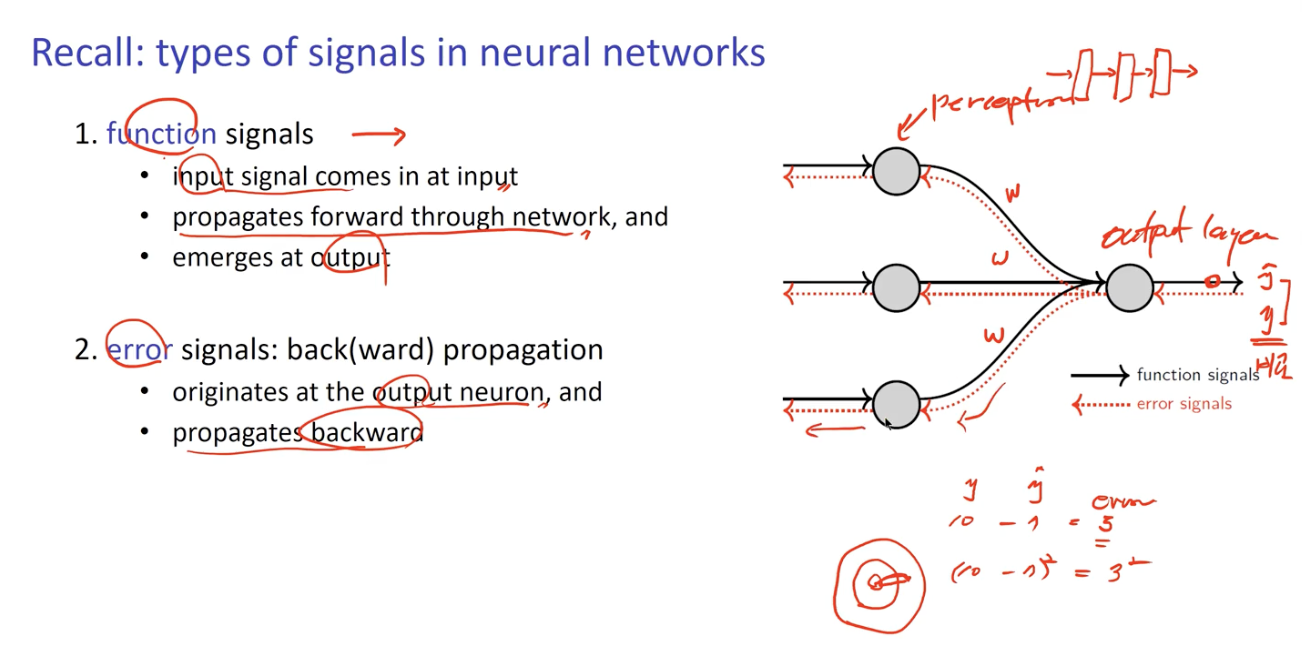
Types of signals in neural networks

1. Function Signal

이전에 배운것.

• Input 으로 Input signal 이 들어와 Output 으로 Output signal 이 나가는 것. (Forward)

2. Error Signal

우리가 원하는 값과 실제 결과 값을 비교하여 Error signal 을 찾아낼 수 있음.

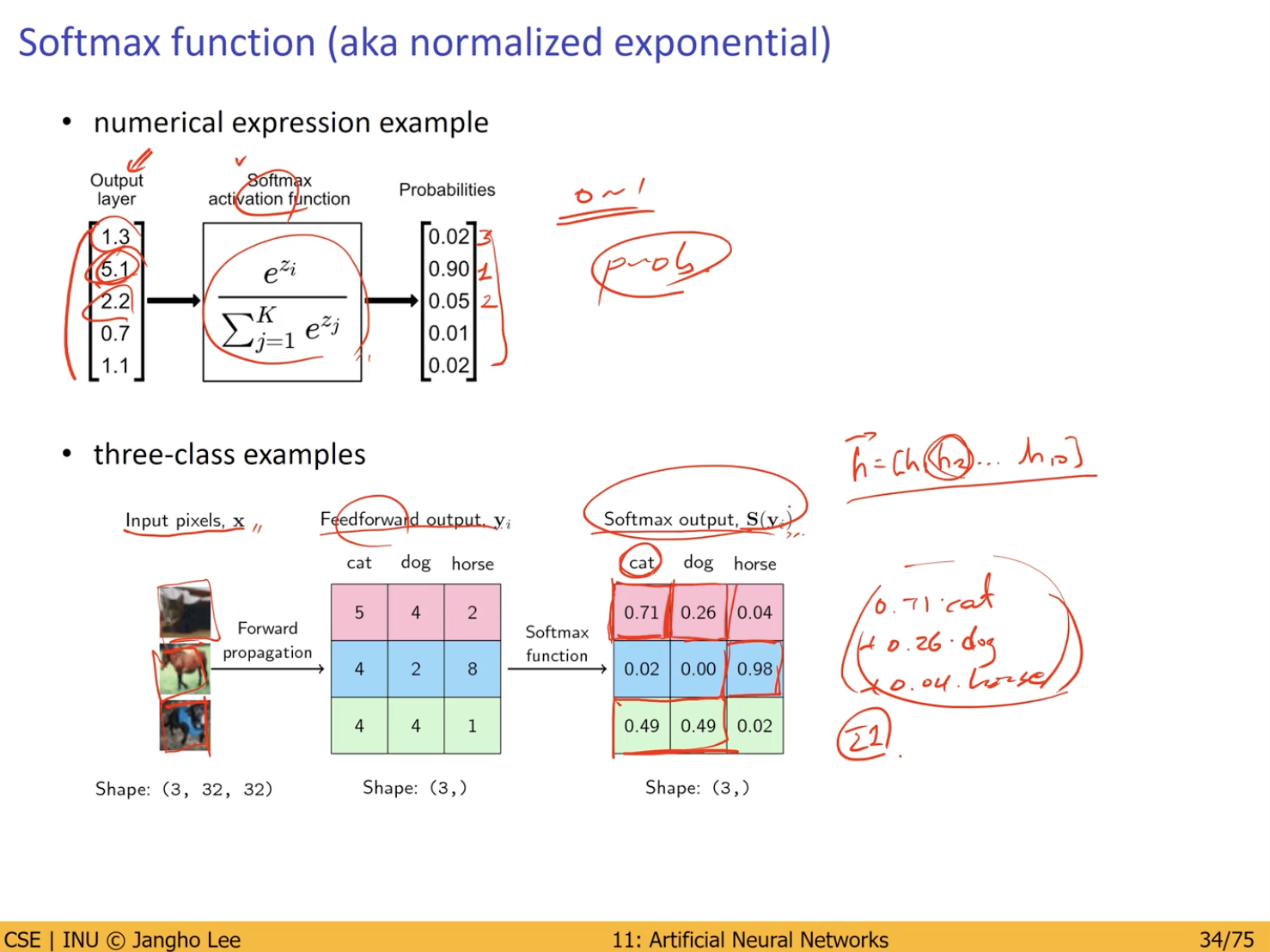
Softmax Function

10개 클래스가 도출되어 10차원의 Vector 로서 데이터가 생성된 경우, 각 데이터를 표현하기 위해 확률 분포로서 표현해주는 Function.

• 각 Data 에 시그마 함수를 씌워 확률 분포로서 표현.
  • 이 경우 모든 Data 를 더하면 1이 된다. (확률 분포로서 표현된 데이터 이므로)

Softmax function 예시

기존 Data 에 Softmax 를 씌우더라도 Data 간의 크기 순서는 변하지 않는다.

• 각 Data 의 값을 0 ~ 1 사이의 확률적 값으로 변환 시켜주는 것.

Softmax Function 후 도출된 Data 에 대한 일반적인 해석

• 특정 Class 의 확률 값이 높다면, Input Data(이미지)는 해당 Class 일 확률이 높다.

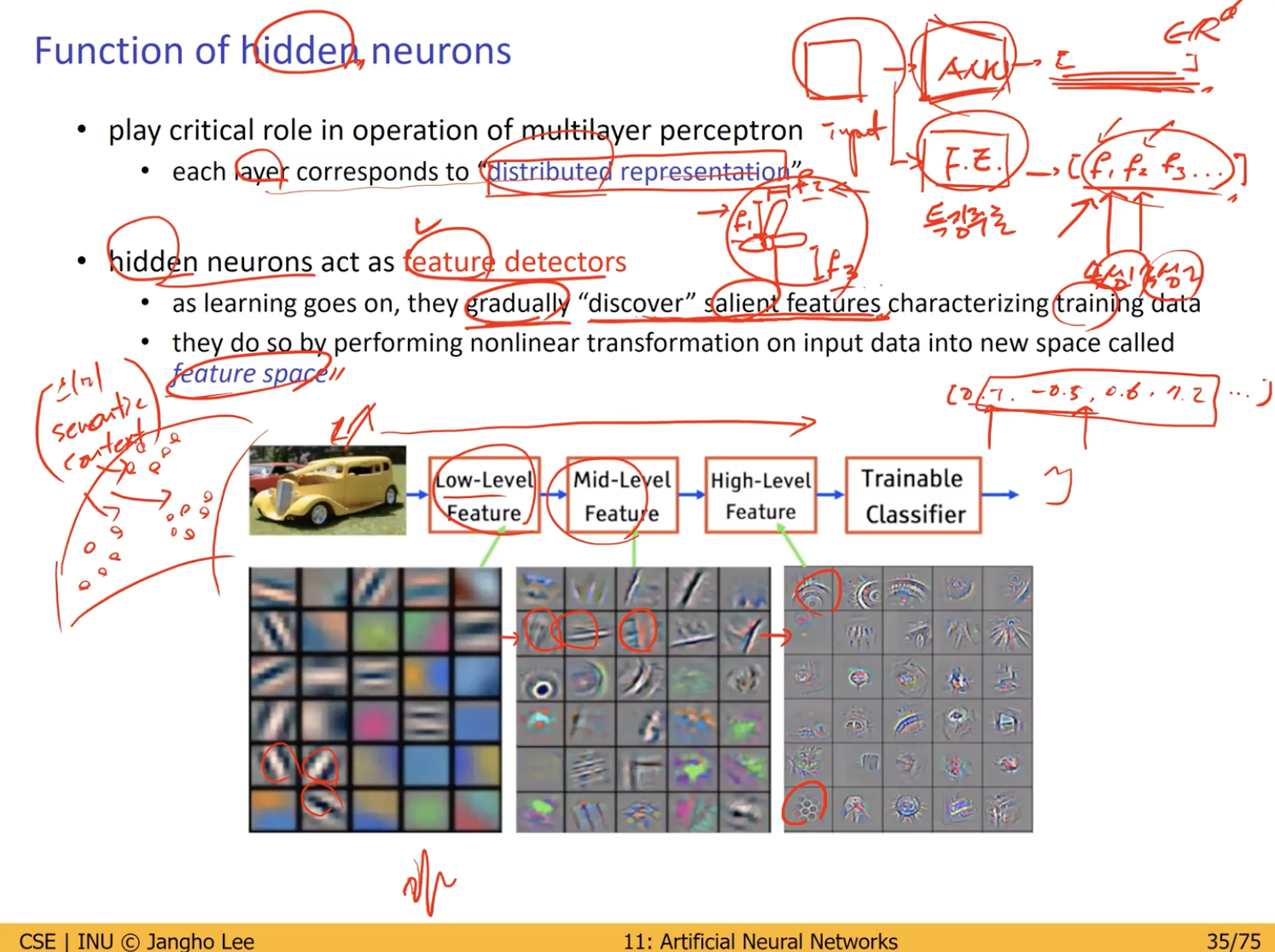
Function of Hidden Neurons

이렇게 추출한 Data 들은 그 자체로서 Data 를 표현하지는 못하지만 해당 Data 들은 실제 Data 들이 녹아들며 만들어진 것이므로 해당 Data 들의 군집을 통해 Image(Data) 의 특징을 뽑아 낼 수 있다.

Multilayer Perceptron

Neural network 에서 Signal 의 Type

1. Function Signal
   • input 으로 input signal 이 들어와 network 를 타고 전방으로 전파되어 나가며 output 으로 반환.

   
   
   

2. Error Signal : Back propagation
   • output neuron 으로부터 이전 Layer 로 이동하며 초기값과의 비교를 통해 Error 를 검출

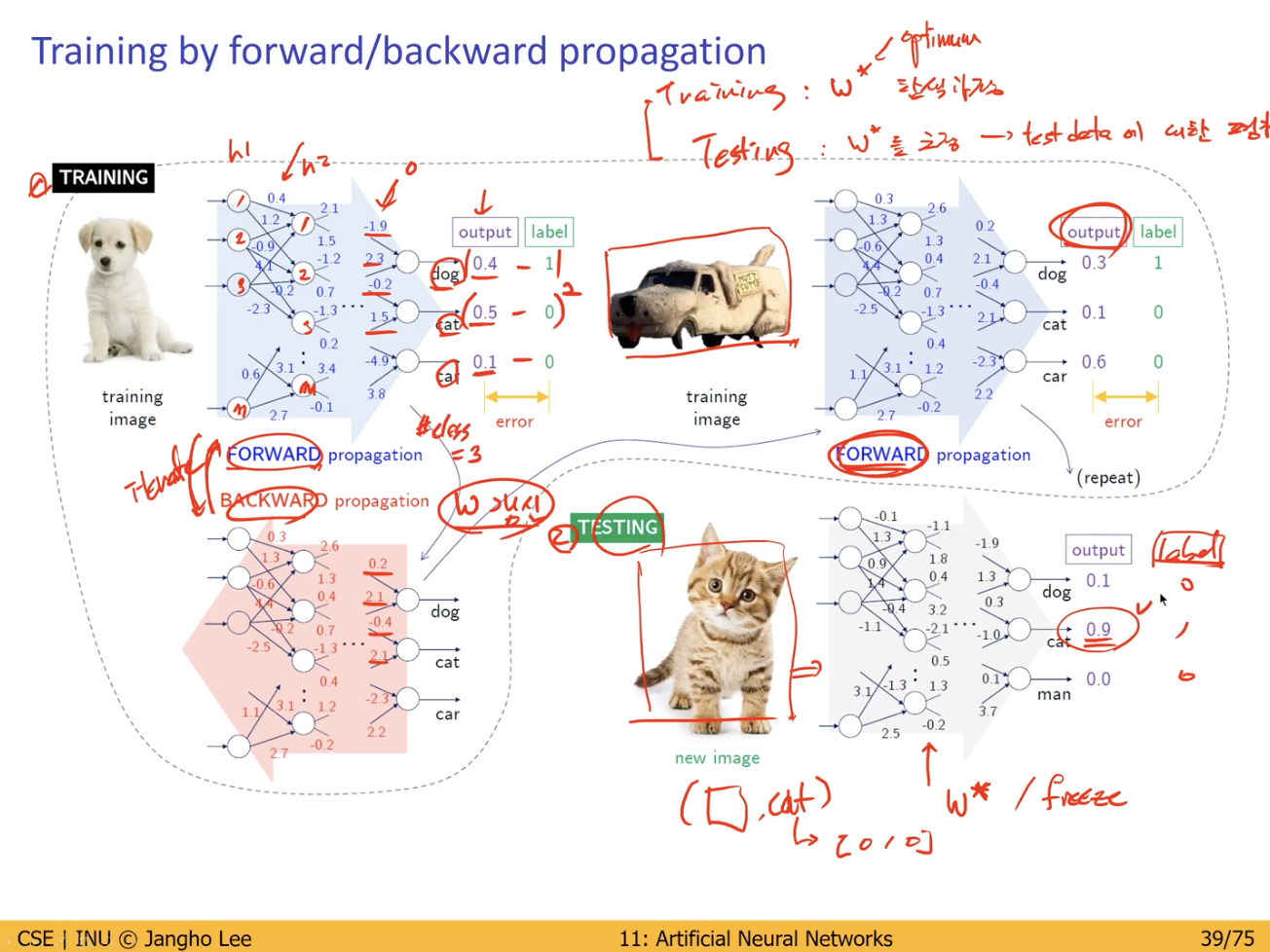
Training by Forward / Backward Propagation

Training 이란 어떤 모델의 가중치를 찾는 과정.

• 최적의 가중치를 탐색하는 과정.

Training 의 과정

1. 주어진 Data를 한번 흘려준다.
   • Model 의 Forward propagation 을 수행.
   • Forward propagation 에 따른 Output 발생.
2. Backward propagation 수행
   • 실제 Data 의 Label 과 Output 간의 차이, 차이의 제곱값, 절대값 등으로 Error 를 정의.
   • Error 에 따라 w(weight) 를 갱신.
3. 1, 2 와 같은 Forward, backward propagation 의 반복을 통해 Model 의 Parameter 를 계속 갱신해나감. (Iterator)
4. Training 이 완료되면 Model 에 최적화된 w(weight) 값이 설정된다.
   • w 값은 freeze 되어 있음.

Test 란 가중치를 고정한 상태에서 우리가 가지고 있는 Test Data 에 대한 평가를 하는 것.

• 위의 Training 과정에서 최적화된 가중치 값을 가지고 있는 Model에 새로운 Test Data(image) 를 Input으로 입력하여 Test를 수행.

Assumptions and Notations

d-H-K neutral network (MLP: Multilayer Pereptron)

• d: 입력의 차원
  • 주어진 Data 에서 추출해낸 특징의 개수만큼 입력의 차원이 존재.
• H: input 과 output 사이의 hidden layer 의 개수
• K: Output 의 개수.
  • Output 은 Class 의 개수만큼 반환.
  • Data 를 몇 개의 Class 로 구분할 것인지를 나타냄.

가중치 표현 방식

• input x_i 와 hidden layer 의 neuron_j 사이의 가중치는 다음과 같이 표현한다.
  • w_ji (Backward 방향으로 index 를 표기)

Model 의 가중치 정의

• (x -> z) 의 가중치 = w_1
  • d x H Matrix 로서 표현 가능
• (z -> h) 의 가중치 = w_2
  • H x K Matrix 로서 표현 가능.
• 따라서, Model 의 총 Parameter (w) 는 다음과 같이 정의할 수 있다.
  • H = {w_1, W_2}

Error measures

세 가지 Error measure 이 존재.

1. e_k
   • e_k : k 번째 Output 에 대한 Error signal.
     • Output_k 와 실제 Data 의 차이를 나타냄.
2. E_n
   • E_n : 많은 Data 중 n 번째 Data 에 대한 Error signal 의 총합.
     • 한 Data 에 대한 모든 e_k 의 총합.
     • n 의 크기에 영향을 받음.
3. E_D
   • E_D : 모든 Data 의 Error signal 총합.
     • 모든 Data 에 대한 E_n 의 총합.
     • 전체에 대한 Error 를 나타냄.

지식 공유 및 기록을 위한 컴퓨터 비전 개인 학습 포스트입니다. 피드백은 항상 환영합니다! 긴 글 읽어주셔서 감사합니다.

처음으로~

Task Lists

• Artificial neural networks (ANNs)
• Models of a Neuron
• Activation function
• Multilayer Perceptron
• Single-layer feedforward network
• Multilayer feedforward network (Multilayer Perceptron)
• Types of signals in neural networks
• Softmax Function
• Function of Hidden Neurons
• Multilayer Perceptron
• Training by Forward / Backward Propagation
• Assumptions and Notations
• Error measures