Linear Regression

5 minute read

Learning Problem

Learning from Data

인간의 학습
나무를 예로 들자면, 인간은 나무를 특별히 학습하지 않더라도 살아가는 과정에서 나무를 보고 접하며 학습 하게 될 수 있다.
즉, Data 를 통해 학습 할 수 있다.
이처럼, 특정 학습을 위해 어떠한 수학적인 Function을 구축하는 것은 쉽지 않다.
대신 이 과정을 여러 Historical Data 를 통해 학습 시킬 수 있다.

Problem Setup

Learning Problem 을 어떻게 Setup 하는가?

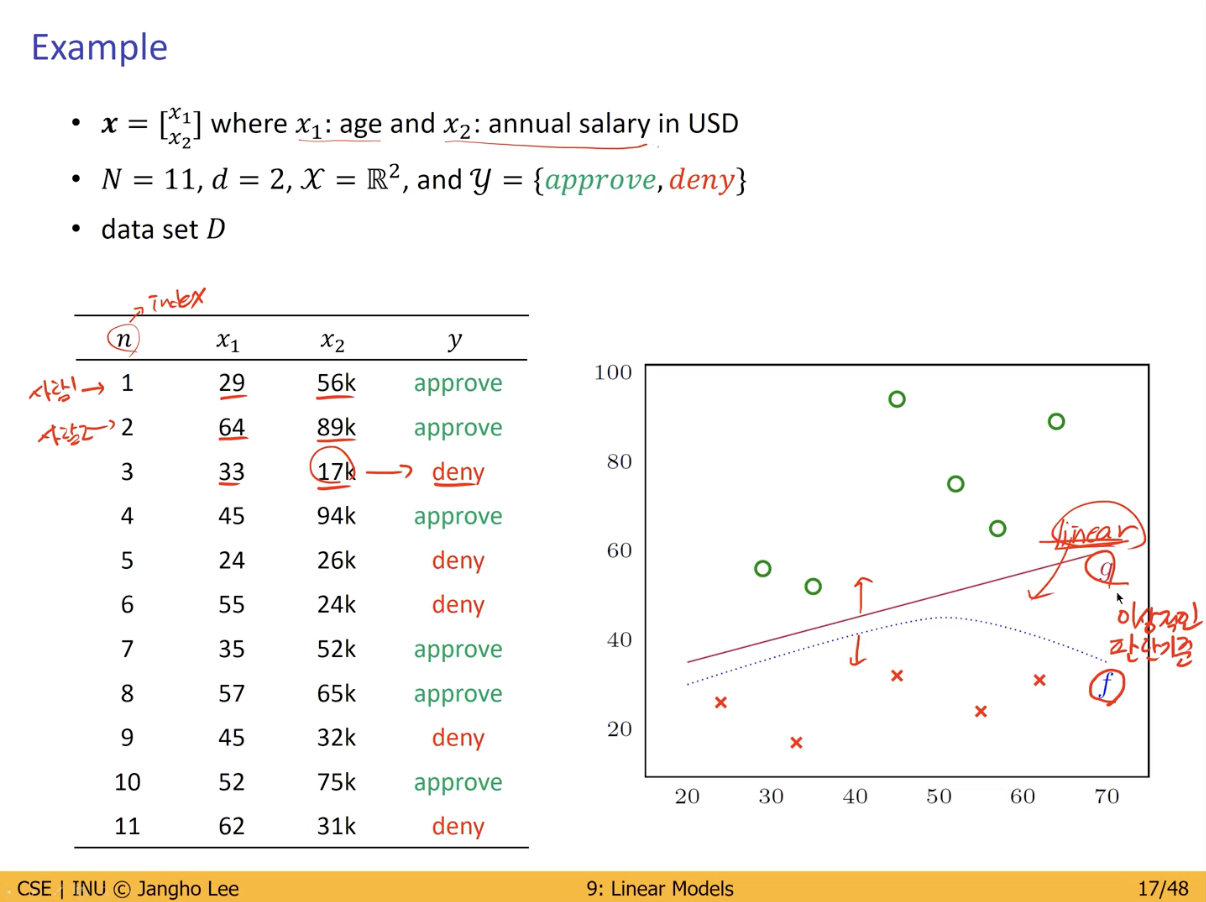
Credit Approval

각 Data 의 확실한 특징을 설정.

Component Symbol Credit Approval Metaphor

Input x(Vector) customer application

Output y approve or deny

Target Function f:x -> y ideal credit approval formula

Data (x1, y1) , … , (xn, yn) historical records

Hypothesis g: x -> y formula to be used

Input

x : Vector
Output

y : Binary 값.

승인 여부
Target Function

우리가 정답이라고 생각하는 것. (Oracle)

실제 정답에 해당되는 것들의 분포.
Data

각각의 Data
Hypothesis

g

우리가 맞추어야 하는 F (Target Function) 를 근사, 모사하도록 학습이된다.

Component	Symbol	Credit Approval Metaphor
Input	x(Vector)	customer application
Output	y	approve or deny
Target Function	f:x -> y	ideal credit approval formula
Data	(x1, y1) , … , (xn, yn)	historical records
Hypothesis	g: x -> y	formula to be used

우리는 Target Function 에 해당되는 정답이란 것을 수학적으로 정의하기는 어려움.
해당 Target Function 을 대신 할 수 있는 Hypothesis (g) 를 생성.
- g 에 대한 Input(x) 을 통해 얻은 Output(y) 의 정확도를 높이기 위한 Parameter 를 설정하게 되는 것.

Credit Approval 예시

이성적인 판단 기준 (정답) 은 F 이나, 이를 수학적으로 정의하기 어려움.

따라서 F에 근접한 Hypothesis (g) 를 가장 기본적인 구조인 Linear (Model) 로서 표현.

Learning Algorithm (Model)

Learning Algorithm (Model) 생성이란?

Hypothesis (g)를 생성하는 것.

Data 를 이용하여 f 에 근접한 g 라는 Folmula 를 생성.
여러 Hypothesis 가 모여있는 그룹을 Hypothesis Set (H) 라고 함.

H 에서 Best Hypothesis (g) 를 선정.

Basic Setup

이전까지 설명한 내용을 표로서 위와 같이 표현 할 수 있다.

Learning Model

Learning Problem 의 세 가지를 정의.

Target Function (f)

Training Examples (Data)

Learning Algorithm(A), Hypothesis Set (H)

사용자가 정하는 것.

어떤 Model 을 사용 할 것인지.

Hypothesis Set

Hypothesis Set H 는 h(x) 로서 구체화됨.

또한 h(x) 는 항상 H 에 포함됨.
h(x)

x 로부터 각각의 다른 weights(= Parameter) 를 받게 됨.

예를 들어 y = ax + b 인 경우 Parameter 는 {a, b}

a 와 b 의 값에 따라 선의 기울기가 달라진다.

Perceptron

Agenda of Perceptron

Linear Model 의 가장 기본적인 형태.

인공 신경망, AI 등의 기본이 되는 Unit 이 Perceptron.

선형 분류기

선으로서 분리되지 못하는 Data Set 의 경우가 존재하면 학습이 불가능함.
어떠한 Input 에 대해 판단을 내리기 위해서는 특정 기준 값이 필요함.

Input Data 의 속성 값이 숫자로서 표현되고 가중치와 같은 속성이 존재하게 되면 특정 기준 값과 비교하여 True / False 로서 판단이 가능하게 됨.

학습이 되어야 할 Parameter 값에서 threshold (기준 값) 를 Subtract 한 결과의 부호로서 판단.
sign 함수

y = sign(a)

a 가 음수인 경우 y = -1

a 가 양수인 경우 y = 1

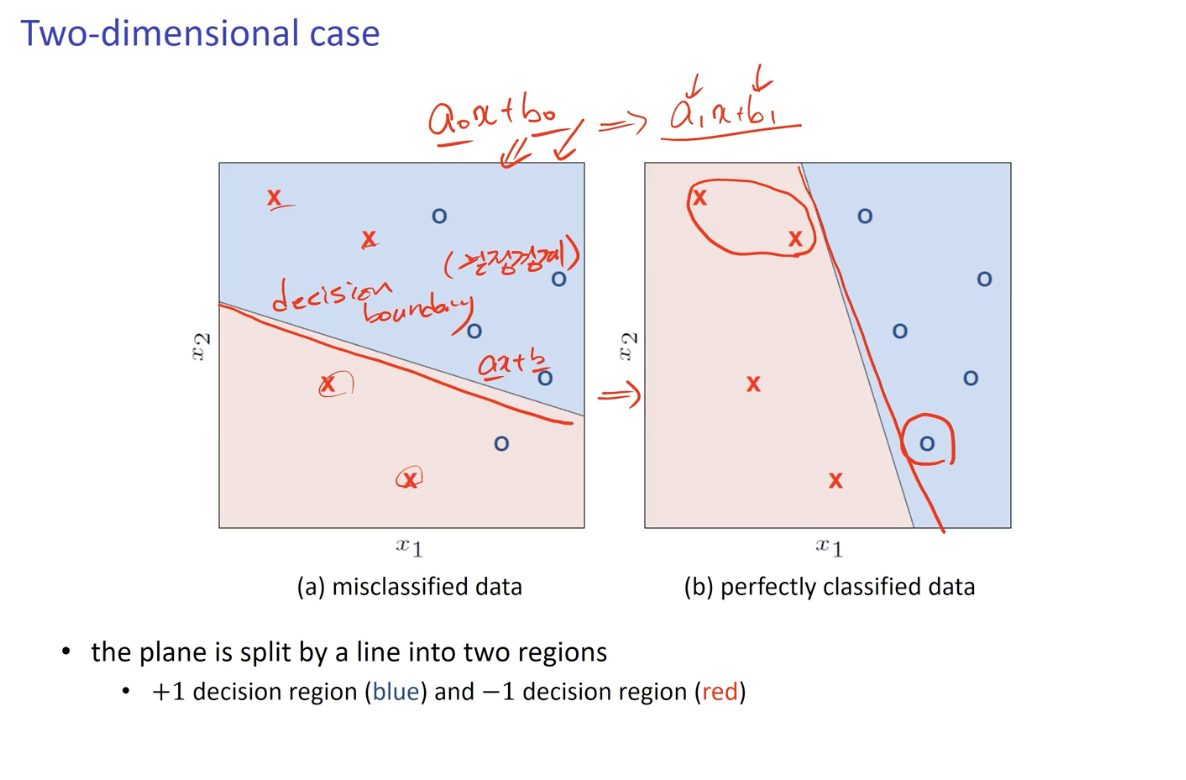
Two-dimensional Case - 결정 경계 (Decision Boundary)

결정 결계 (Decision Boundary)

2차원 에서 정의되는 y = ax + b 라는 기준 선.
Learning Algorithm 이 하는 역할은 Parameter(weights) 의 설정

Data Set 에 맞춰 적절히 작동하도록 결정 경계선의 기울기(parameter. {a, b})를 찾아가는 Algorithm.

Learning Algorithm 에 의해 찾은 이상적인 Parameter 는 Hypothesis(g) 가 된다.

g 는 Opimal Choice 가 된다. (가장 이상적인 결정 경계 직선)

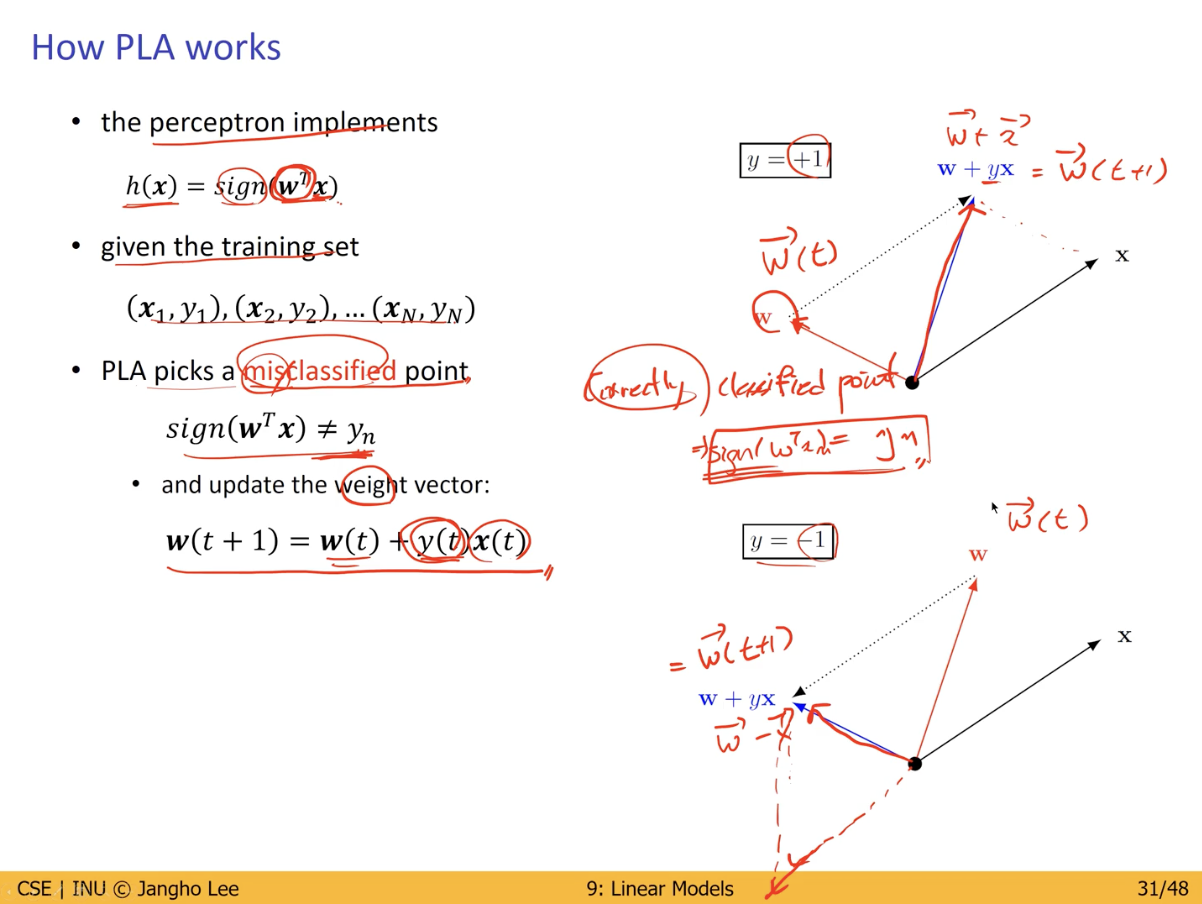
Perceptron Learning Algorithm (PLA)

Hypothesis(g) 를 생성하기 위하여 가지고 있는 Data Set 에 대해 가장 이상적인 결정 경계를 생성 할 수 있는 Parameter (w) 를 결정하는 알고리즘.

위처럼 주어진 Perceptron 의 weight 를 sign 함수의 값에 따라 업데이트 해가며 이상적인 weight 를 찾아간다. (Iteration 을 통해서)

Linear Classification

Classification 이란 Category 를 분류하는 것.

Linear Model for Binary Classification

가장 쉬운 Classification.

Binary, 즉 0과 1 (-1 or 1) 두개의 Category 로 분류.

Perceptron 을 활용.

Vector 로서 존재하는 Data 를 특정 공간 d 에 Mapping 시켜 생성되는 Output y 를 h(x) = sign(w^T x) 을 활용하여 분류.

Reality : 선형 분류의 한계 (In-sample Error & Out-of-sample Error)

하지만 이상과 현실은 다르다.
실제 데이터들은 매우 혼잡한 상태로 분포하며, 아주 이상적인 경우를 제외하고 선형적으로 분리되기 어려움.
In-sample Error

기존에 가지고 있는 Data Set 에 대한 Error.
Out-of-sample Error

한번도 보지 못한 새로운 Data 에 대한 Error.
위와 같은 Error 는 Linear Classification 에서 필연적으로 발생할 수 밖에 없다.

Linear Classification 이 될 법도 한데, 아주 작은 Noise 때문에 실패 할 수도 있음.

따라서, Error 를 최대한 줄일 방법을 모색해야함.

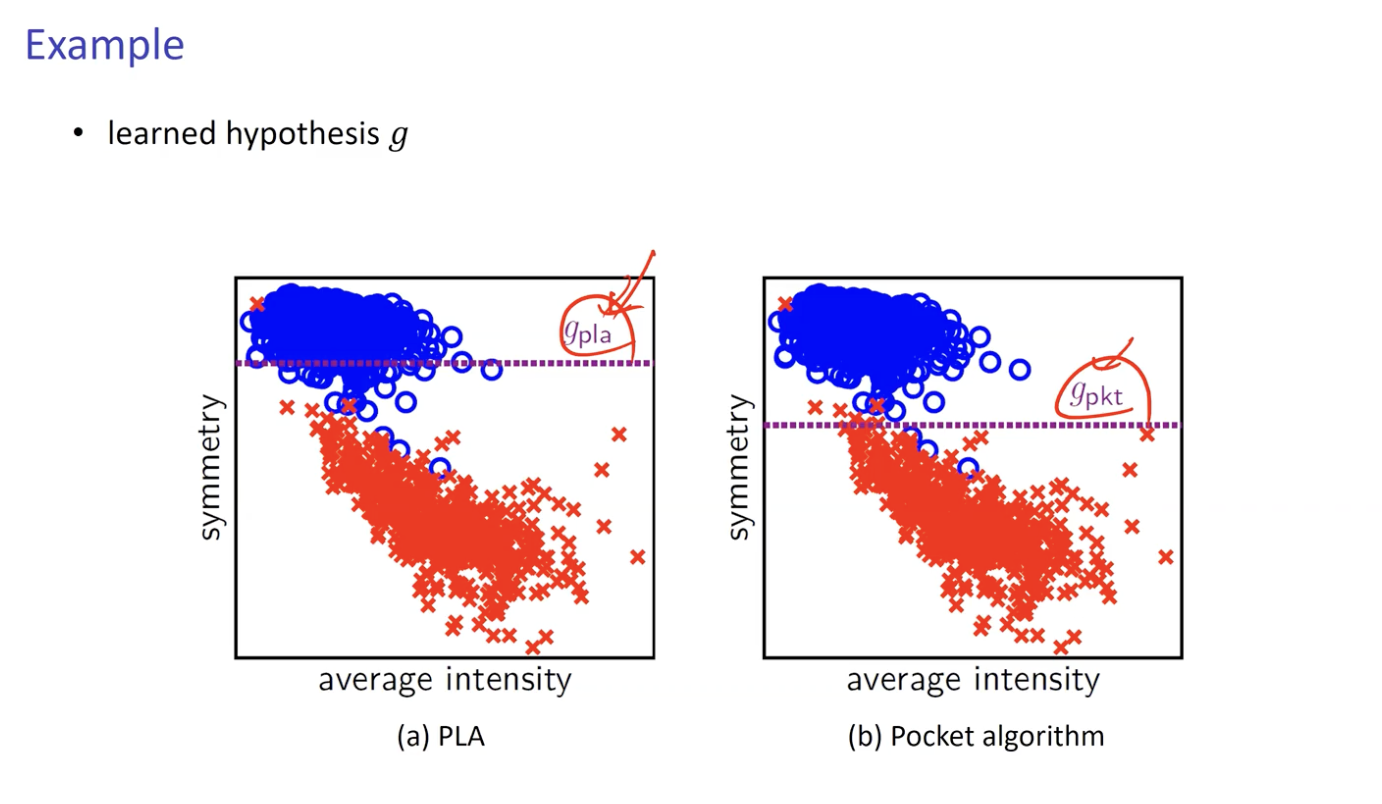
Pocket Algorithm

Error 발생을 최소화 하기 위해 모색한 방법 중 하나.
이상적인 결정 경계선을 찾는 과정 중 Pocket 공간에 가장 이상적인 선(weight) 을 저장해둔다.

가장 이상적인 weight 는 Error 발생이 가장 적은 weight

set the pocket weight vector 𝒘 to 𝒘(0) of PLA
for (𝑡𝑡 = 0, … , 𝑇𝑇 − 1) do
    run PLA for one update to obtain 𝒘(𝑡 + 1);
    evaluate 𝐸𝑖n(𝒘(𝑡 + 1);     /* time consuming */
    if (𝑤(𝑡 + 1) is better than 𝒘 in terms of 𝐸𝑖n)
        then set 𝒘 to 𝒘(𝑡 + 1)
return 𝒘;

Line 4 에서 모든 데이터를 비교하기 때문에 PLA 보다는 시간 소요가 크다.

PLA 와 Pocket Algorithm 의 모습

Linear Regression

이전에 학습한 내용에서는 f(x) = y 이며 이에 근사한 결과를 도출하기 위해 g(x) = y 를 찾아 y 값에 따라 적절히 Classification 했으나, Regression의 경우 y 값이 정수가 아닌 실수(Real Number)로서 도출되어 명확한 Classification 이 불가한 경우이다.

f 에 약간의 Noise 가 추가되어 있는 경우.

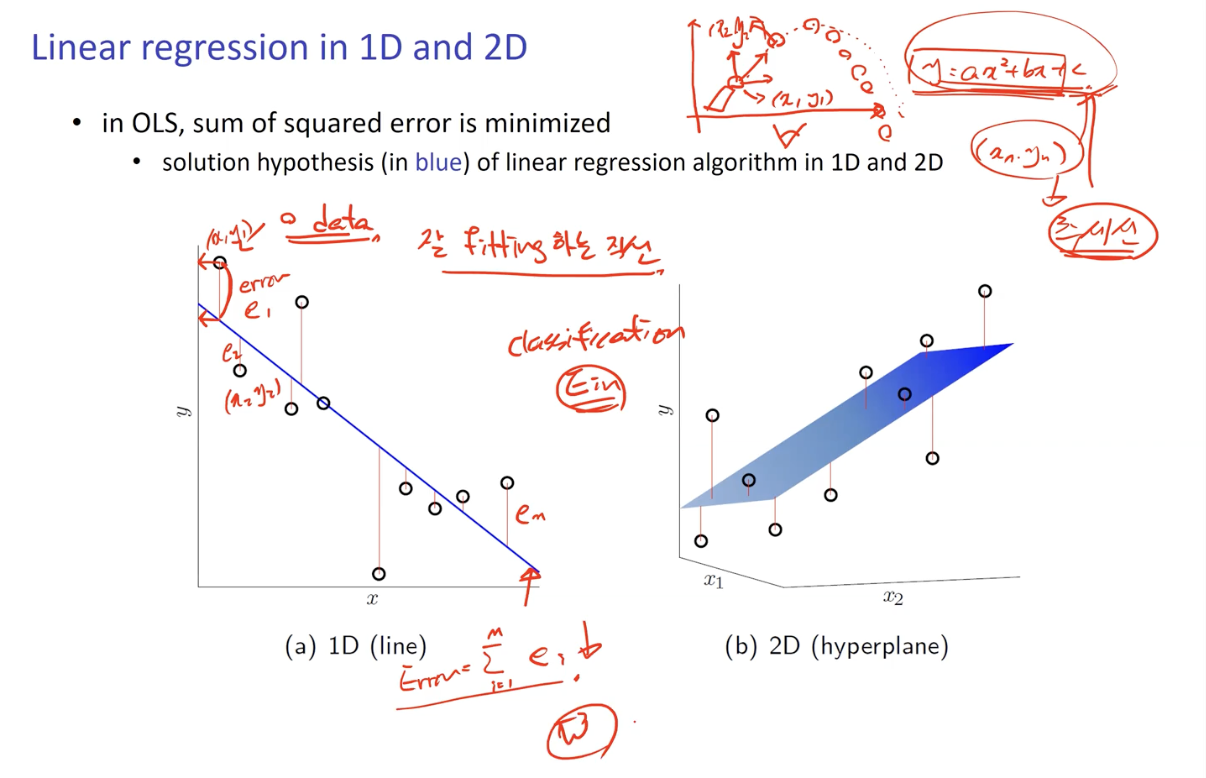
Linear Regression in 1D & 2D

Data 를 1차원 공간에 Mapping 하였을 시 분포하는 좌표 지점과 g 의 그래프 (선) 간의 오차가 Error 이다.
모든 Error 를 더한 값이 총 Error 크기가 되고, 그 크기가 가장 적게 나타나는 직선을 선택하게 된다.

Getting the Solution w

그렇다면 해당 Error 가 최소화 되는 직선은 어떻게 구할 것인가?

변수가 하나인 경우

미분을 사용하여 곡선 그래프를 직선 형태로 만들어 0이 되는 지점을 찾으면 최소값을 찾을 수 있다.

변수가 두 개인 경우

Gradient 를 취하여 결과 값이 0이 되는 곳이 최소값.

Linear Model 요약

Linear Model 생성 방법의 종류

Classification

Regression
특징

Parameter 개수가 적기 때문에 복잡도가 낮으며 학습 시간이 빠르다.

어떤 Data Set 을 학습할 때에 가장 먼저 적용시켜 보기 좋은 Model.

Signal 을 사용.

우리가 가지고 있는 Data Set 과 Linear Model Parameter 간의 내적