Chae Seungmin

DevOps & carefree life [TMON] Channel Service Dev. Team

5 minute read

Data Structure :: 순환 (Recursion)

Data Structure : 순환(Recursion) 이란?

recursion_Procdess사진출처:datatrained

“순환이란, 어떤 알고리즘이나 함수가 자기 자신을 호출하여 문제를 해결하는 프로그래밍 기법이다.”
📣 순환은 본질적으로 순환적인 문제나, 그러한 자료구조를 다루는 프로그램에 적합하다. 📣

순환의 예

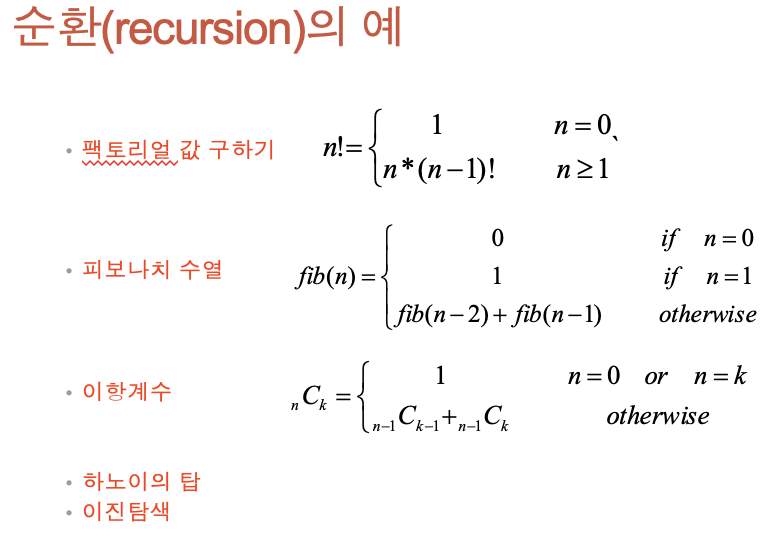
순환(Recursion)의 예

recursionex_Procdess순환적인 문제의 예

팩토리얼 프로그래밍(Factorial Programming)

팩토리얼 프로그래밍을 해보자.

factorial_Procdessfactorial의 정의

  • 정의: Factorial n! 을 정의하는 과정에서 다시 Factorial (n-1)! 이 사용되었다.
    이것에 유의하여 아래 코드를 보도록 하자.
  • 우선 팩토리얼 프로그램의 알고리즘은 아래와 같다.

    팩토리얼 프로그래밍 #1: 
(n-1)! 팩토리얼을 구하는 서브 함수 factorial_n_1를 따로 제작
(n-2)! 팩토리얼을 구하는 서브 함수 factorial_n_2를 따로 제작
.
.
.
(반복)

    int factorial(int n) // 우리는 매개변수로 n을 받아 n!을 출력하는 프로그램을 만들었다.
{
if( n<= 1 ) return(1);
else return (n * factorial_n_1(n-1) ); // 팩토리얼의 정의.
}
// 그렇다면 매개변수인 n 만 n-1 로 바꾸어 주면 (n-1)! 을 구할 수 있을 것이다!




    팩토리얼 프로그래밍 #2: 
(n-1)! 팩토리얼을 현재 #1 에서 작성중인 함수를 다시 호출하여 계산 (순환 호출)

    int factorial(int n) 
{
  if( n <= 1 ) return(1);
  else return (n * factorial(n-1) ); //#1 에서 작성한 
                                    //factorial(int n) 함수를 재사용 했다.
}

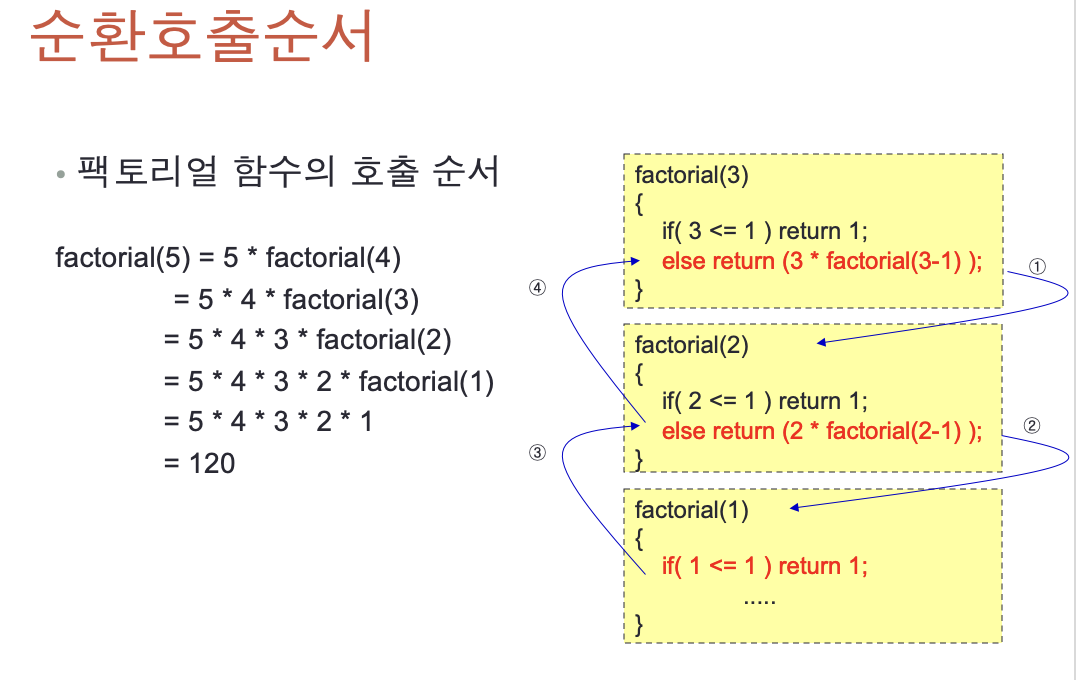
Factorial 함수의 호출 순서

factorialfunc_Procdessfactorial 함수의 호출 순서

순환 알고리즘의 구조

  • 순환 알고리즘은 다음과 같은 부분들을 포함한다.
    • 순환 호출을 하는 부분.
    • 순환 호출을 멈추는 부분.
int factorial(int n){
  if(n<=1) return 1; // 순환을 멈추는 부분.
  
  else return n * factorial(n-1); // 순환 호출을 하는 부분
}

🔥만약 순환 호출을 멈추는 부분이 없다면 시스템오류가 발생할 때까지 무한정 호출하게 된다.🔥

순환 / 반복

"되풀이" 는 컴퓨터 알고리즘에서 흔하게 볼 수 있는 알고리즘이며,
그 방법에는 '반복(Iteration)' 과 '순환(recursion)' 이 있다.

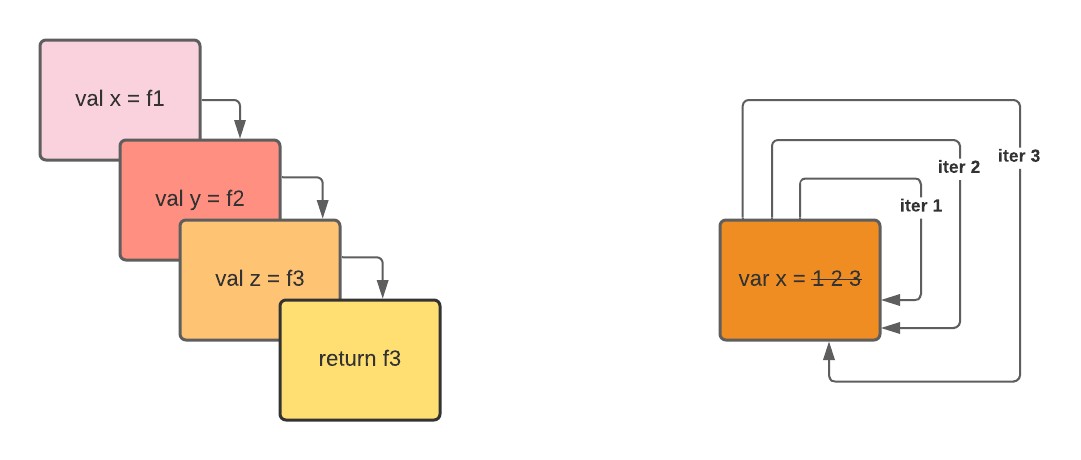
RecIter_Procdess왼쪽이 Recursion, 오른쪽이 Iteration사진출처:edward-huang

순환(Recursion)

  • 주어진 task를 수행하기 위하여 자기 자신을 다시 호출(순환 호출)하여 작업을 수행해 나가는 방식이다.
  • 순환은 본질적으로 순환적(Rcursive)인 문제나 그러한 자료구조를 다루는 프로그램에 적합하다.
  • 하지만 자기 자신이란 함수를 반복하여 호출하므로
    반복에 비해 수행속도가 떨어지거나 함수 호출의 오버헤드가 발생할 수 있다.

순환의 원리

Factorial 함수를 잘 보자. 문제를 하나씩 해결한 후에 다음 순환을 실행한다.
이처럼 순환은 주어진 문제를 조금씩 해결한 후 동일하지만 더 작은 문제들로 분해하여 해결한다.
이를 우리는 분할정복(Divide and conquer) 이라고 한다.
순환의 가장 중요한 점은 순환호출이 일어날 때마다 문제의 크기가 작아져 결국엔 아주 풀기 쉬운 문제가 된다는 점이다.


faciter_ProcdessFactorial 함수를 Iterator 로 작성한 모습.

반복(Iteration)

  • 반복이란 for, while 등의 반복구조로 되풀이하는 방법이다.
  • 변수를 사용하여 일정 횟수의 반복이나 어떠한 조건을 만족시킬 때까지 반복시킨다.
  • 간단명료하며 빠르고 효율적으로 되풀이를 수행할 수 있지만 순환적인 문제에서는 프로그램 작성이 어려울 수도 있다.

기본적으로 반복과 순환은 문제 해결 능력이 같다.
모든 순환은 반복으로 작성 할 수 있으며, 대부분의 반복은 순환으로 작성할 수 있다. 😀

반복 사용의 예 - 피보나치 수열

Fibonacci_Procdess피보나치 수열의 정의(Fibonacci numbers)

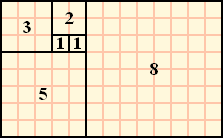
FibonacciBlocks_Procdess피보나치 수열로 사각형 채우기
사진출처:wikipedia

  • 피보나치 수열은 바로 앞 두개의 숫자를 더해서 뒤의 숫자를 만들어 나가는 수열이다.
  • 정의를 보면 정의 자체가 순환적으로 되어 있다. 순환 호출을 사용해보자.

    int fib(int n)
{
  if( n==0 ) return 0;
  if( n==1 ) return 1;
  return (fib(n-1) + fib(n-2)); // 순환
}    // 시간복잡도: 한 수가 한번 호출되면 다시 두 번 호출되므로, 
   // O(2^{n})으로 나타낼 수 있다.

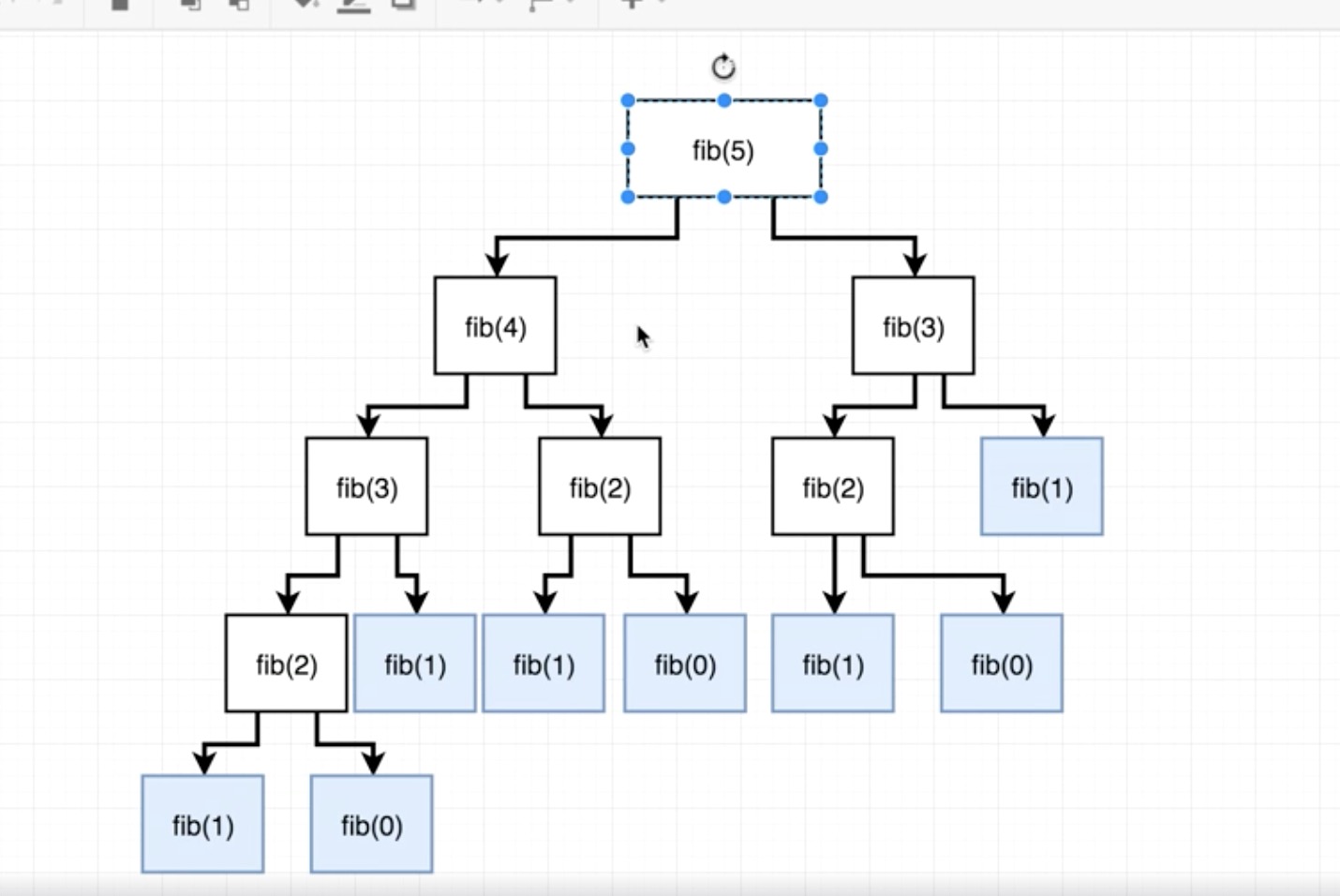
    recfib_Procdess
    피보나치 수열의 결과
    사진출처:stackoverflow

  • 그러나 위 결과를 보아, 피보나치 수열에 순환을 사용했을 경우 매우 비효율적이다.
  • 같은 항이 중복하여 계산되고 있으며, 이 현상은 n이 커질수록 더욱 심각해진다.
  • 그렇다면 반복(Iterator)을 사용해보자.

    fib_iter(int n) {
  if( n < 2 ) return n;            // 비교 연산 + 1
  else {
      int i, tmp, current=1, last=0; // 대입 연산 + 4
      for(i=2;i<=n;i++){             // loop 문은 시간복잡도 계산시 미포함
          tmp = current;               // 대입 연산 + n
          current += last;             // 대입 연산 + n
          last = tmp;                  // 대입 연산 + n
      }
      return current;
  }
}           // 시간복잡도: 3n + 5 = O(n) 으로 나타낼 수 있다.

시간복잡도를 근거로, 피보나치 수열은 순환이 아닌 반복을 사용할 경우 가장 이상적인 것을 알 수 있다. 😊

순환 사용의 예 - 하노이 탑

hanoi_Procdess
하노이 탑
사진출처:wikipedia

  • 순환의 사용 예로 가장 적절한 것은 바로 "하노이 탑 문제" 이다.
  • 문제는 첫번째 막대에서 세번째 막대로 원판을 옮기는 것이다.

조건
한 번에 하나의 원판만 이동할 수 있다.
맨 위에 있는 원판만 이동 할 수 있다.
크기가 작은 원판위에 큰 원판이 쌓일 수 없다.
중간의 막대를 임시적으로 이용할 수 있으나 앞의 조건들을 지켜야 한다.

앞서 알아봤던 것처럼, 순환이 일어날수록 문제의 크기가 작아져야 한다.

  • 여기서 문제의 크기는 이동하여야 하는 디스크의 개수 가 된다.
  • 이제 문제를 나누어서 생각해보자.
    N개의 원판이 막대 A에 쌓여있는 경우,
1. 위에 쌓여 있는 N-1개의 원판을 막대 B로 옮긴다.(가장 밑의 원판을 남겨두고)
2. 이후 가장 밑의 원판을 막대 C로 옮긴다. (목적지)
3. 막대 B에 쌓여있는 N-1개의 원판들을 막대 C로 옮겨준다.
  • 여기서 궁금증이 들 것이다.

    “그러니까 N-1개를 막대 B로 어떻게 옮기냐는 말이냐구요 ㅋㅋ..”

    "정답"

  • 방금 당신은 정확히 순환(Recursion)을 필요로 한 것이다.
  • 문제를 다시 보면, N-1개의 원판들을 다시 다른 막대로 옮기는 작업은
    우리가 기존에 했던 N에 대한 작업과 같은 작업이다.

🤬 아직 이해가 안된다면, 아래 코드를 같이 보도록 하자.

C언어: 하노이 탑 구현

// sudo 코드로 구현한 하노이 탑
// 막대 from에 쌓여있는 n개의 원판을 막대 tmp를 사용하여 막대 to로 옮긴다.

void hanoi_tower(int n, char from, char tmp, char to) { 
   if (n==1){ 
       from에 있는 한 개의 원판을 to로 옮긴다. 
   } else{ 
       1. from의 제일 밑 원판을 제외한 나머지 원판들을 tmp로 옮긴다.
       2. from에 있는 한 개의 원판을 to로 옮긴다. 
       3. tmp의 원판들을 to로 옮긴다.
   } 
}




// C언어를 이용하여 구현한 하노이 탑
// 막대 from에 쌓여있는 n개의 원판을 막대 tmp를 사용하여 막대 to로 옮긴다.

void hanoi_tower(int n, char from, char tmp, char to) { 
   if (n==1){ 
       from에서 to로 원판을 옮긴다. 
   } else{ 
       hanoi_tower(n-1, from, to, tmp); // 자신의 매개 변수를 n-1로 할당하여 순환
       from에 있는 한 개의 원판을 to로 옮긴다. 
       hanoi_tower(n-1, tmp, from, to); // 자신의 매개 변수를 n-1로 할당하여 순환
   }
}



이제 위의 아이디어를 가지고 최종 프로그램을 작성해보자. 

#include <stdio.h>
void hanoi_tower(int n, char from, char tmp, char to) {

  if( n==1 ) printf("원판 1을 %c 에서 %c으로 옮긴다.\n",from,to);

  else {
	hanoi_tower(n-1, from, to, tmp); // 순환 호출
	printf("원판 %d을 %c에서 %c으로 옮긴다.\n",n, from, to);
	hanoi_tower(n-1, tmp, from, to); // 순환 호출
  }
}

void main() {
    hanoi_tower(4, 'A', 'B', 'C');
}



결과:
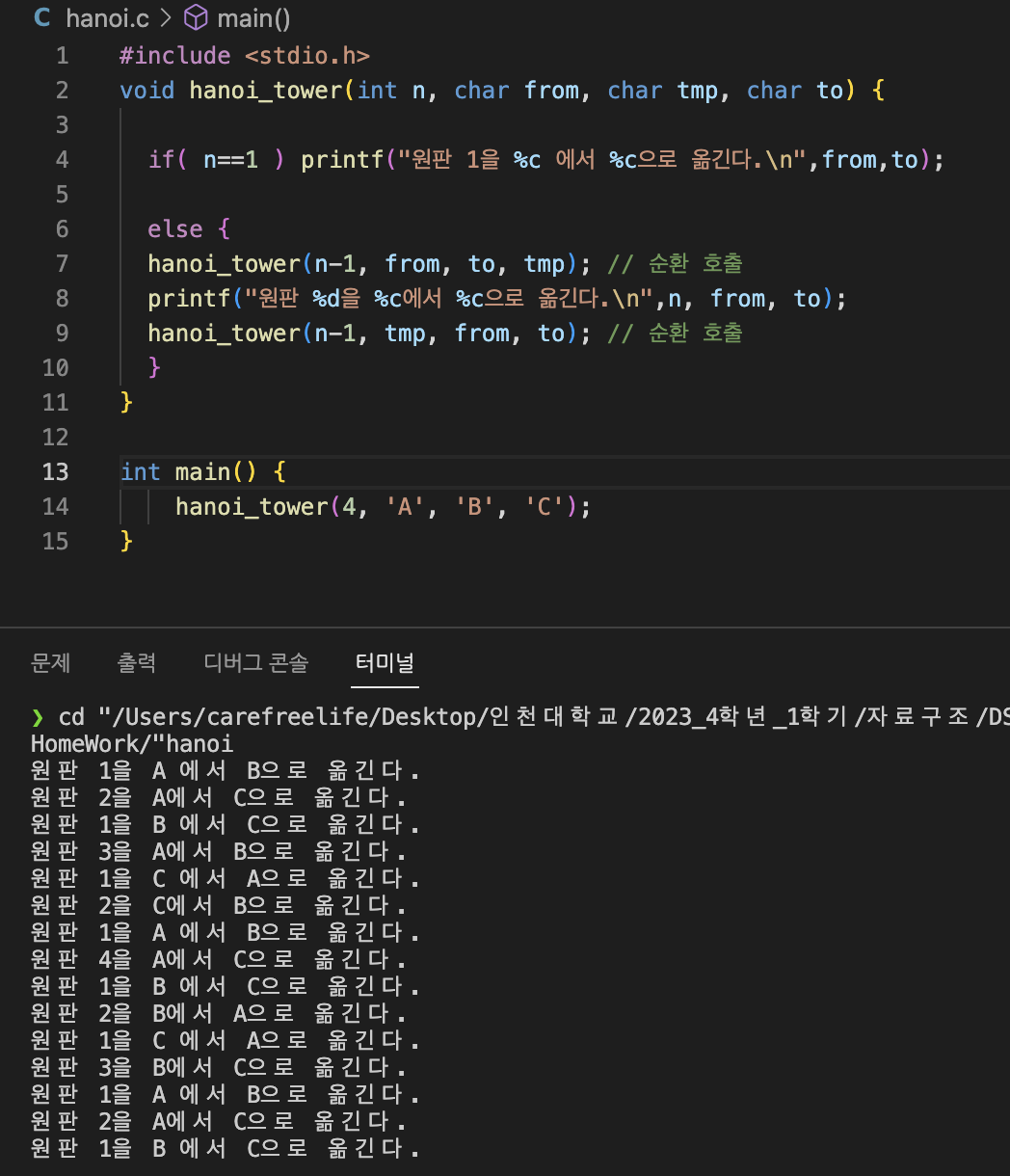
rshanoi_Procdess
C 언어로 구현한 하노이 탑

이상으로 자료구조 - 순환 포스팅을 마친다.

처음으로~

참고: C언어로 쉽게 풀어쓴 자료구조 <개정 3판> 천인국, 공용해, 하상국 지음


Task Lists

  • Data Structure : 순환(Recursion) 이란?
  • 순환(Recursion)의 예
  • 팩토리얼 프로그래밍을 해보자.
  • 순환 알고리즘의 구조
  • 순환 / 반복
  • 순환의 원리
  • 반복 사용의 예 - 피보나치 수열
  • 순환 사용의 예 - 하노이 탑
  • C언어: 하노이 탑 구현

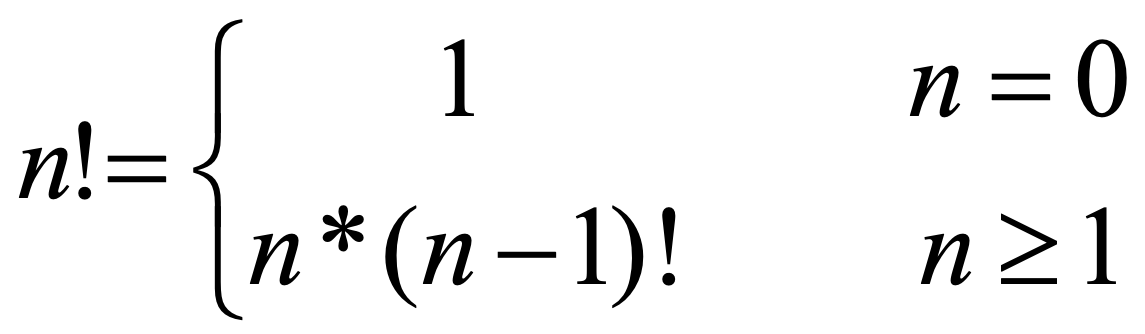
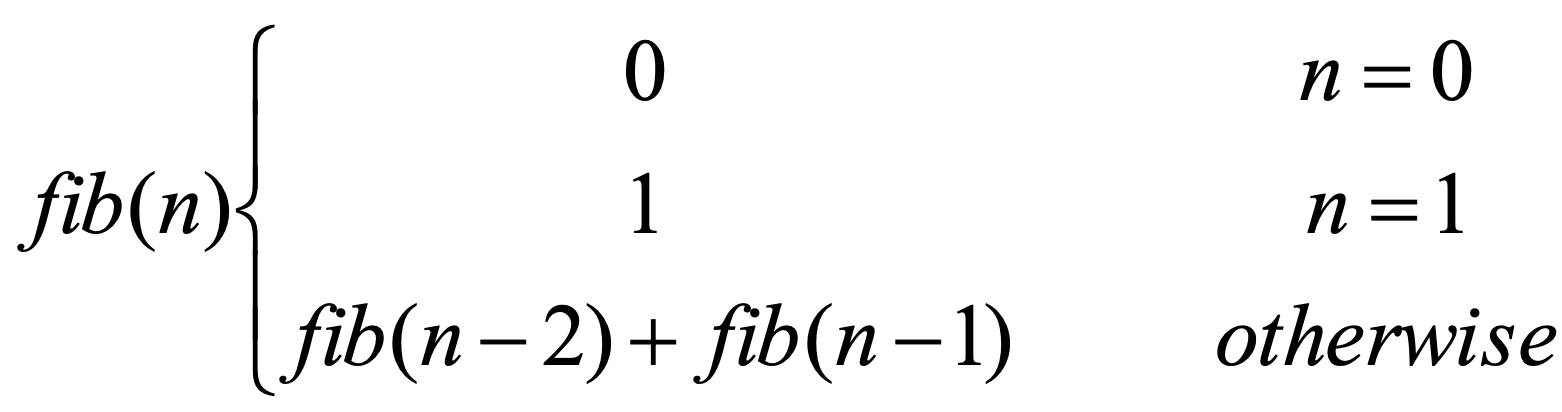
Comments

You May Also Enjoy