Data Structure - 이진 탐색 트리 (Binary Search Tree) 란?

8 minute read

이진 탐색 트리 (Binary Search Tree) 란?

이진 탐색 트리 (Binary Search Tree) 는 이진 트리 기반의 탐색을 효율적으로 하기 위한 자료 구조.
  - 모든 원소의 key는 유일한 key를 가진다.(Primary Key)
  - 왼쪽 서브 트리 key들은 루트 key보다 작다.
  - 오른쪽 서브 트리의 key들은 루트의 key보다 크다.
  - 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
  - 위와 같은 성질은 이진 탐색 트리 내의 모든 노드에서 만족.

따라서, 찾고자 하는 key값이 루트 노드의 key값과 비교하여,
루트 노드의 key값보다 작으면 왼쪽 서브트리, 크면 오른쪽 서브트리를 탐색.
위 과정을 탐색이 성공할 때까지 반복하면 쉽게 원하는 key값을 가진 노드를 찾을 수 있다.

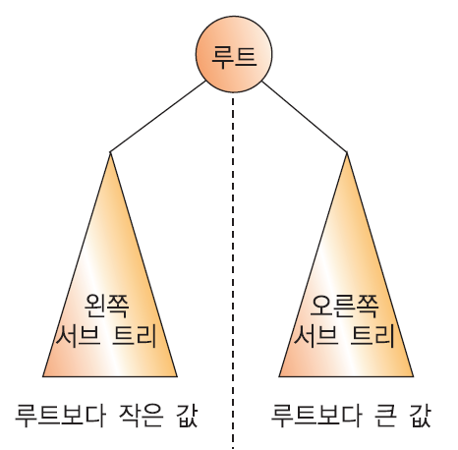
이진 탐색 트리의 정의

각 노드가 가진 key(Primary Key)를 이용하여 특정한 key를 가진 노드를 찾는다.

key(왼쪽 서브 트리) <= key(루트 노드) <= key(오른쪽 서브 트리)

이진 탐색 트리를 중위 순회하면 오름차 순으로 정렬된 key 값을 얻을 수 있다.

위와 같은 성질은 모든 이진 탐색 트리에서 만족

이진 탐색 트리에서의 탐색 연산 (순환 / 반복)

1. 순환적인 탐색 연산

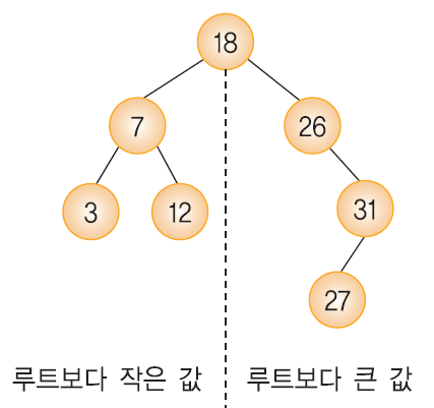
이진 탐색 트리의 탐색 과정

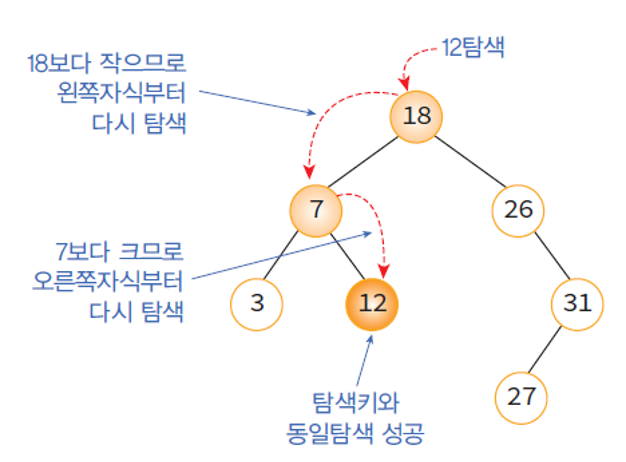
현재 노드의 key값과 원하는 노드의 key값을 비교한 결과가 같으면 탐색이 성공적으로 끝난다.

비교한 결과가,

주어진 key값이 루트 노드의 key값보다 작으면 해당 루트 노드의 왼쪽 자식을 기준으로 다시 탐색 시작.

주어진 key값이 루트 노드의 key값보다 크면 해당 루트 노드의 오른쪽 자식을 기준으로 다시 탐색 시작. ```java // 순환적인 탐색 함수 TreeNode *search(TreeNode *root, int key){ if(root == NULL) return NULL; // 주어진 key와 같은 key를 가진 node가 없으면 탐색 실패. NULL 반환 if(key == root->key) return root; // 주어진 key와 현재 node의 키가 같으면 탐색 성공. 현재 node를 반환.

// 주어진 key가 현재 node의 key보다 작으면 현재 노드의 왼쪽 서브 트리에 값이 있으므로 // 현재 노드의 왼쪽 자식을 기준으로 다시 탐색. else if (key < root->key){ search(root->left, key); } // 주어진 key가 현재 node의 key보다 크면 현재 노드의 오른쪽 자식을 기준으로 다시 탐색. else { search(root->right, key); } } ```

2. 반복적인 탐색 연산

이진 탐색 트리를 탐색하는 방법에는 반복적인 방법도 존재한다.

효율성을 따지면 반복적인 함수가 훨씬 우수하다고 한다.

// 반복적인 탐색 함수
TreeNode *search(TreeNode *root, int key){
// 알맞은 범위(작으면 왼쪽 서브트리, 크면 오른쪽 서브 트리)에 맞게 단말 노드까지 내려가며 탐색.
while(root != NULL){
    // 주어진 key와 현재 노드의 key값이 같으면 탐색 성공. 현재 노드를 반환.
    if(key == root->key){
        return root;
    }
    // 주어진 key가 현재 노드의 key보다 작으면 왼쪽 서브트리 탐색.
    else if(key < root->key){
        root = root->left; // 현재 노드를 가리키고 있는 포인터를 왼쪽 자식을 가리키도록 한다.
    }
    // 주어진 key가 현재 노드의 key보다 크면 오른쪽 서브트리 탐색.
    else{
        root = root->right; // 현재 노드를 가리키고 있는 포인터를 오른쪽 자식을 가리키도록 한다.
    }
}
// while문 중간에 알맞은 노드를 찾아 return 되지 않고 NULL 값인 단말 노드까지 탐색 후
// 반복이 종료되면 탐색 실패. NULL 반환.
return NULL; 
}

이진 탐색 트리에서의 삽입 연산

"이진 탐색 트리에 원소를 삽입하기 위해서는 항상 탐색을 수행하는 것이 선행" 되어야 한다.

Why? 1. 이진 탐색 트리에서는 "같은 키 값을 갖는 노드" 가 없어야 하기 때문.
     2. 탐색을 수행하며 "탐색을 실패한 위치에 새로운 노드를 삽입" 하기 때문.

BSTreeSearch_Procdess
이진 탐색 트리에서의 삽입 연산

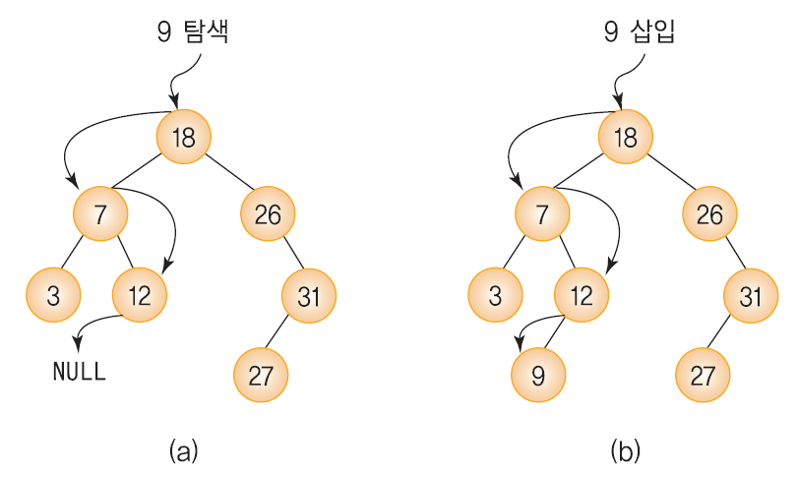
루트 노드에서부터 단말 노드까지 9를 탐색하여 같은 key(9)값을 가진 노드가 있는지 확인한다.
- 같은 key 값을 가진 노드가 있으면 삽입불가.
- 없으면 단말 노드까지 탐색을 수행하다가 실패하는 지점에 key(9)를 가진 노드를 삽입.
- 새로운 노드는 항상 단말 노드로서 추가된다.

// 이진탐색트리 삽입 프로그램

TreeNode* insert_node(TreeNode* node, int key){
  // 트리가 공백이거나 탐색에 실패하여 삽입 할 위치를 찾으면 새로운 노드를 반환한다.
  if(node == NULL){
      return new_node(key); 
  }
  // 트리에 노드가 존재한다면, 순환적으로 트리를 타고 내려간다.
  if(key < node->key){
      node->left = insert_node(node->left, key);
  }
  else if(key > node->key){
      node->right = insert(node->right, key);
  }
  return node; // 변경된 루트 포인터를 반환한다.  
}

// 위에서 사용된 new_node(key) 함수는 동적으로 메모리를 할당하여 새로운 노드를 생성 및 반환하는 유틸리티 함수이다.
TreeNode* new_node(int key){
  TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
  node->key = key;
  node->left = node->right = NULL;
  return node;
}

이진 탐색 트리에서의 삭제 연산

이진 탐색 트리에서 "가장 복잡한 연산은 노드의 삭제 연산" 이다.

"탐색" 을 통해 삭제하려는 노드를 찾은 후, 다음과 같은 "3가지의 경우를 고려" 해야 한다.
1. 삭제하려는 노드가 "단말 노드" 일 경우.
2. 삭제하려는 노드가 "왼쪽이나 오른쪽 서브 트리 중 하나만 가지고" 있는 경우.
3. 삭제하려는 노드가 "두 개의 서브 트리 모두 가지고" 있는 경우.

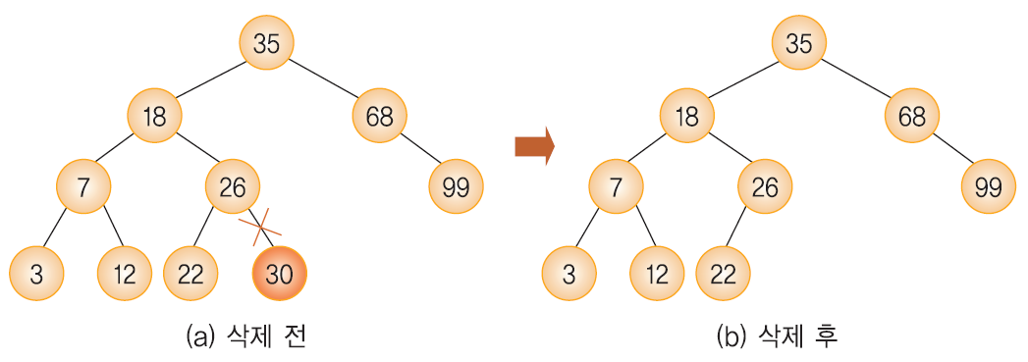
Case 1: 삭제하려는 노드가 단말 노드일 경우

이진 탐색 트리에서의 삭제 연산 - 단말 노드

단말 노드는 자식 노드가 없기에 해당 단말 노드만 삭제하면 된다.

단말노드의 삭제 과정

해당 단말 노드의 부모를 찾는다.

단말노드와 연결된 부모노드의 링크 필드를 NULL로 설정하여 연결을 끊는다.

단말 노드에게 할당된 메모리를 반환한다. (노드 동적 생성시)

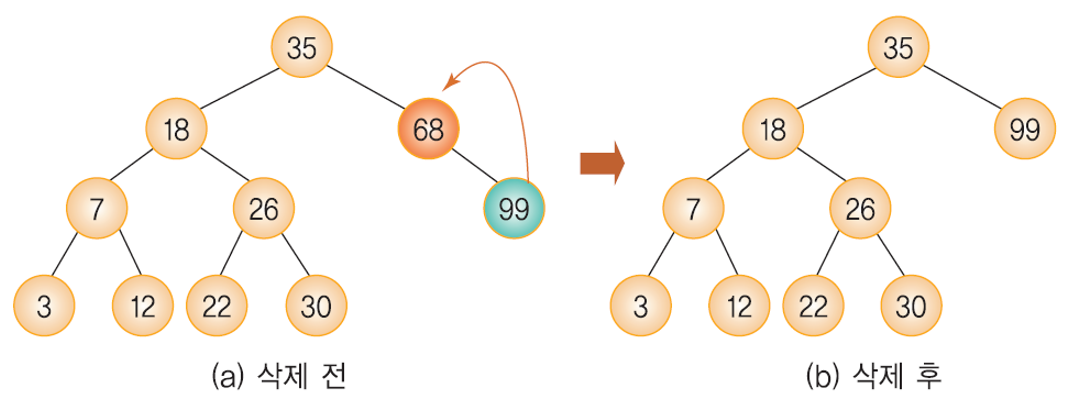
Case 2: 삭제하려는 노드가 하나의 서브 트리만 가지고 있는 경우

이진 탐색 트리에서의 삭제 연산 - 하나의 서브트리를 가지고 있는 경우

삭제될 노드가 하나의 서브 트리를 가지고 있는 경우,
자기 자신(노드)을 삭제하고 자신의 서브 트리를 자신의 부모 노드에게 붙여주면 된다.

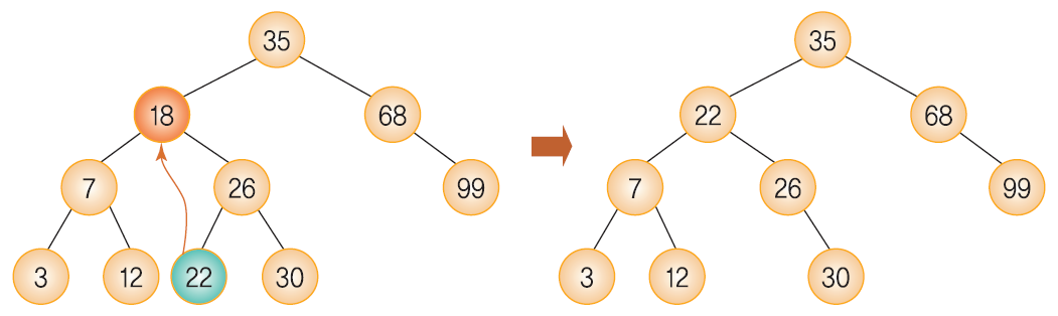
Case 3: 삭제하려는 노드가 두 개의 서브 트리 모두 가지고 있는 경우

이진 탐색 트리에서의 삭제 연산 - 두 개의 서브트리 모두 가지고 있는 경우

관건은 “두 개의 서브트리 중 어떤 노드를 삭제 노드 위치로 가져올 것인가” 이다.

삭제되는 노드와 가장 값이 근접한 노드를 가져와야 한다.

삭제될 노드와 가장 비슷한 값을 가진 노드 - 후계자 노드

왼쪽 서브트리의 가장 오른쪽 노드

오른쪽 서브트리의 가장 왼쪽 노드

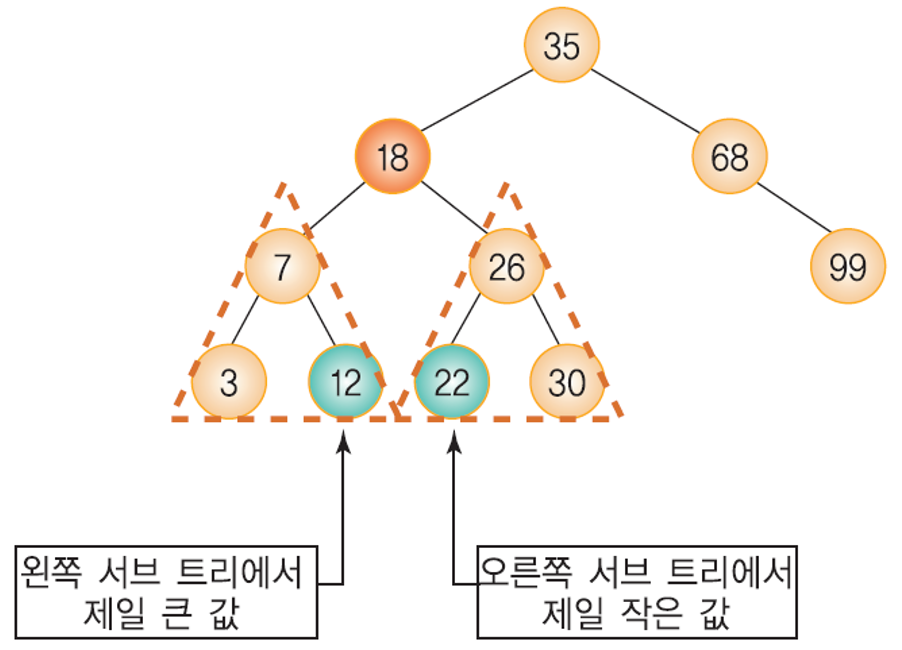
예) 오른쪽 서브트리의 가장 작은 값을 가진 가장 왼쪽의 노드 찾는 법:

오른쪽 서브트리의 왼쪽 링크를 타고 NULL을 만날 때까지 이동.

두 노드 중 어떤 것을 선택하더라도 상관없으나,
여유가 된다면 두 노드 중 기존 노드와 더 근접한 노드를 선택하면 좋다.

이진 탐색 트리를 중위 순회 하였을 때 두 노드는 선행노드와 후속 노드에 해당한다.

두 서브 트리를 가진 노드의 삭제 과정

왼쪽 서브트리의 가장 오른쪽 노드 or 오른쪽 서브트리의 가장 왼쪽 노드를 탐색.

탐색을 통해 찾은 삭제될 노드와 가장 근접한 값을 가진 두 노드중 하나를 노드 삭제 위치에 올린다.

이진 탐색 트리의 삭제 함수도 루트 포인터를 변경시키므로 루트 포인터를 마지막에 반환하여야 한다.
// 이진 탐색 트리에서의 삭제 함수
TreeNode* delete_node(TreeNode* root, int key){
  // 삭제할 노드를 찾지 못하면 NULL 반환
  if(root == NULL) {
      return NULL;
  }
  // 왼쪽 서브트리 탐색
  if(key < root->key){
      delete_node(root->left, key);    
  }
  // 오른쪽 서브트리 탐색
  else if (key > root->key){
      delete_node(root->right, key);
  }
  // 삭제 대상 노드를 찾은 경우
  else {
      // case 1: 단말 노드인경우, case 2: 오른쪽 서브 트리만 있는 경우
      if(root->left == NULL){
          TreeNode* temp == root->right // 삭제되어 반환할 노드 임시 저장
          free(root); // 삭제 대상 노드 메모리 반환
          return temp; 
      }
      else if(root->right == NULL){
          TreeNode* temp == root->left;
          free(root);
          return temp;
      }
      // case 3: 삭제 대상 노드가 두 개의 서브트리를 가지고 있을 때.
      else{
          // min_value_node() 함수를 통해 가장 작은 key값을 가진 노드를 찾는다.
          // 여기서는 삭제 노드의 오른쪽 서브 트리에서 가장 작은 값의 노드를 찾는다.
          TreeNode* temp = min_value_node(root->right);
          // 후계 노드를 복사.
          root->key = temp->key;
          // 후계 노드를 삭제
          root->right = delete_node(root->right, temp->key) 
      }
  }
  return root; // 변경된 루트 포인터를 반환
}

// min_value_node(TreeNode* node) 함수는 
// 주어진 이진 탐색 트리에서 최소 키값(가장 왼쪽 노드)을 가지는 노드를 찾아서 반환한다.
TreeNode* min_value_node(TreeNode* node){
  TreeNode* current = node;
  // 가장 왼쪽 노드를 찾아 내려감.
  while(current->left != NULL){
      current = current->left;
  }
  return current;
}

기본적인 이진 탐색 트리의 전체 프로그램

// 이진 탐색 트리

#include<stdio.h>
#include<stdlib.h>

typedef int element;

typedef struct TreeNode{
    element key;
    struct TreeNode *left;
    struct TreeNode *right;
}TreeNode;

// 순환적인 탐색 함수
TreeNode* search(TreeNode* root, int key){
    if(root == NULL){
        return NULL;
    }
    if(key == root->key){
        return root;
    }
    else if(key < root->key){
        return search(root->left, key);
    }
    else {
        return search(root->right, key);
    }
}

//새 노드 생성 함수
TreeNode* new_node(int key){
    TreeNode* new = (TreeNode*)malloc(sizeof(TreeNode));

    new->key = key;
    new->left = new->right = NULL;

    return new;
}

// 노드 삽입 함수
TreeNode* insert_node(TreeNode* root, int key){
    // 말단 노드까지 탐색 후 주어진 key를 가진 노드가 존재 하지 않으면 새 노드 생성하여 반환.
    if(root == NULL){
        return new_node(key);
    }
    // 말단 노드까지 탐색하여 내려간다.
    if(key < root->key){
        root->left = insert_node(root->left, key);
    }
    else if(key > root->key){
        root->right = insert_node(root->right, key);
    }
    return root;
}

// 가장 작은 key값을 가진 노드 찾기
TreeNode* min_value_node(TreeNode* root){
    TreeNode* current = root;
    // 가장 왼쪽 노드를 찾으러 내려간다. (이진 탐색 트리에서 가장 작은 key 값을 가진 노드는 가장 왼쪽에 있다.)
    while(current->left != NULL){
        current = current->left;
    }
    return current;
}

// 이진 탐색 트리와 키가 주어지면, 해당 키를 가진 노드를 삭제, 새로운 루트 노드 반환
TreeNode* delete_node(TreeNode* root, int key){
    // 탐색 실패. 해당 키를 가진 노드가 없어 삭제 불가 - NULL 반환.
    if(root == NULL){
        return NULL;
    }
    // 탐색 실패가 아니면 해당 노드를 찾아 내려간다.
    if(key < root->key){
        return delete_node(root->left, key);
    }
    else if(key > root->key){
        return delete_node(root->right, key);
    }
    // 탐색에 성공하면 3가지 경우에 따라 노드 삭제를 수행.
    else {
        // 삭제 대상 노드가 말단 노드인 경우 or 오직 하나의 서브 트리만 가지고 있는 경우.
        if(root->left == NULL){
            TreeNode* temp;
            temp = root;
            free(root);
            return temp;
        }
        else if(root->right == NULL){
            TreeNode* temp;
            temp = root;
            free(root);
            return temp;
        }
        // 삭제 대상 노드가 두 개의 서브트리 모두 가지고 있는 경우.
        // 삭제 대상 노드와 가장 근접한 key를 가진 노드를 찾는다.
        // == 왼쪽 서브트리의 가장 오른쪽 노드 or 오른쪽 서브트리의 가장 왼쪽 노드.
        TreeNode* temp = min_value_node(root->right);
        // 삭제 대상 노드에 key값을 복사.
        root->key = temp->key;
        // key값을 복사해온 노드를 삭제한다.
        root->right = delete_node(root->right, temp->key);
    }
    return root;
}

void inorder(TreeNode* root){
    // 노드가 존재하면 실행.
    if(root){
        inorder(root->left);
        printf("[%d] ", root->key);
        inorder(root->right);
    }
}

int main(void) {
	TreeNode * root = NULL;
	TreeNode * tmp = NULL;

	root = insert_node(root, 80);
	root = insert_node(root, 20);
	root = insert_node(root, 40);
	root = insert_node(root, 30);
	root = insert_node(root, 60);
	root = insert_node(root, 70);

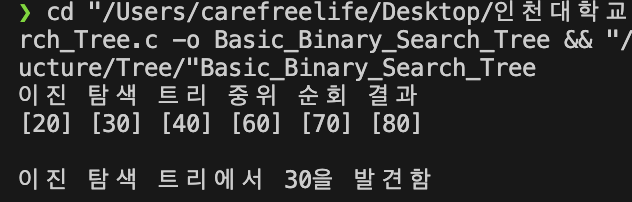
	printf("이진 탐색 트리 중위 순회 결과 \n");
	inorder(root);
	printf("\n\n");
	if (search(root, 30) != NULL)
		printf("이진 탐색 트리에서 30을 발견함 \n");
	else
		printf("이진 탐색 트리에서 30을 발견못함 \n");
	return 0;
}

기본적인 이진 탐색 트리 실행 결과

-> 이진 탐색 트리를 중위 순회 하면 정렬된 데이터를 얻을 수 있다.

이진 탐색 트리의 성능 분석

균형 이진 탐색 트리인 경우 최선의 시간 복잡도를 가진다.

이진 탐색 트리에서의 탐색삽입, 삭제 연산의 시간 복잡도는 트리의 높이에 비례한다.

트리의 높이가 h이면, O(h) 가 된다.

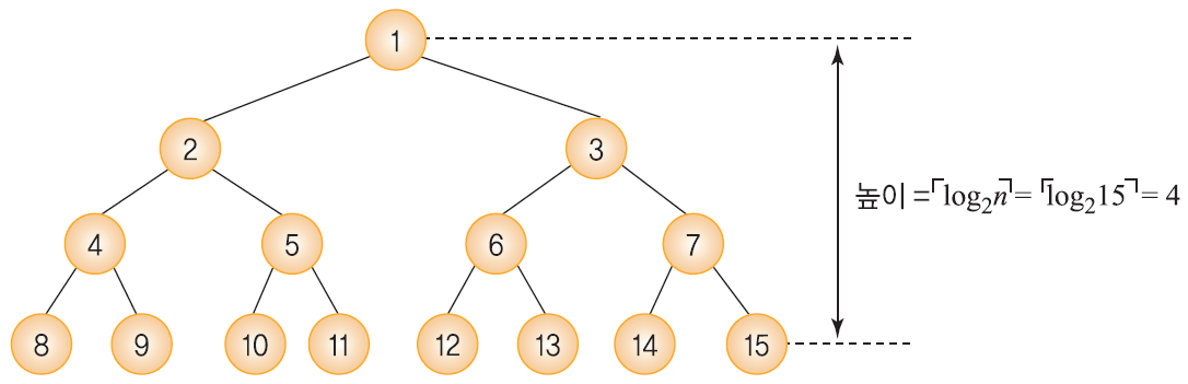
n개의 노드를 가지는 이진 탐색 트리의 경우, 일반적인 이진 트리의 높이는 ⌈log_2 n⌉.

따라서, 이진 탐색 트리 연산의 시간 복잡도의 최선은 O(log_2 n)이다.
기본적인 이진 탐색 트리 실행 결과

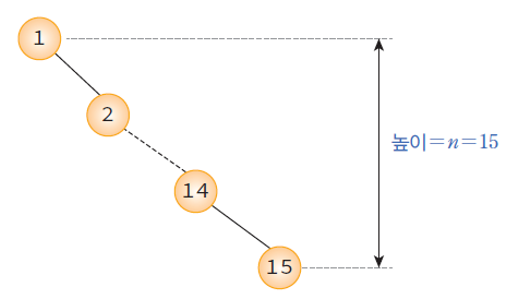
최악의 경우(경사트리), O(n) 까지 가능.

순차 탐색과 시간 복잡도가 같다.

최대한의 설명을 코드 블럭 내의 주석으로 달아 놓았습니다.

혹시 이해가 안가거나 추가적인 설명이 필요한 부분, 오류 등의 피드백은 언제든지 환영합니다!

긴 글 읽어주셔서 감사합니다. 포스팅을 마칩니다.

처음으로~

참고: C언어로 쉽게 풀어쓴 자료구조 <개정 3판> 천인국, 공용해, 하상국 지음

Task Lists

이진 탐색 트리 (Binary Search Tree) 란?
이진 탐색 트리에서의 탐색 연산 (순환 / 반복)
이진 탐색 트리에서의 삽입 연산
이진 탐색 트리에서의 삭제 연산
기본적인 이진 탐색 트리의 전체 프로그램
이진 탐색 트리의 성능 분석

Twitter Facebook LinkedIn

Chae Seungmin

Data Structure - 이진 탐색 트리 (Binary Search Tree) 란?

이진 탐색 트리 (Binary Search Tree) 란?

이진 탐색 트리에서의 탐색 연산 (순환 / 반복)

이진 탐색 트리에서의 삽입 연산

이진 탐색 트리에서의 삭제 연산

기본적인 이진 탐색 트리의 전체 프로그램

이진 탐색 트리의 성능 분석

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)

※블로그 이전 안내※

Chae Seungmin

이진 탐색 트리 (Binary Search Tree) 란?

이진 탐색 트리에서의 탐색 연산 (순환 / 반복)

이진 탐색 트리에서의 삽입 연산

이진 탐색 트리에서의 삭제 연산

기본적인 이진 탐색 트리의 전체 프로그램

이진 탐색 트리의 성능 분석

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)