Data Structure - 그래프 (Graph) 란? (1)

13 minute read

그래프 (graph) 란?

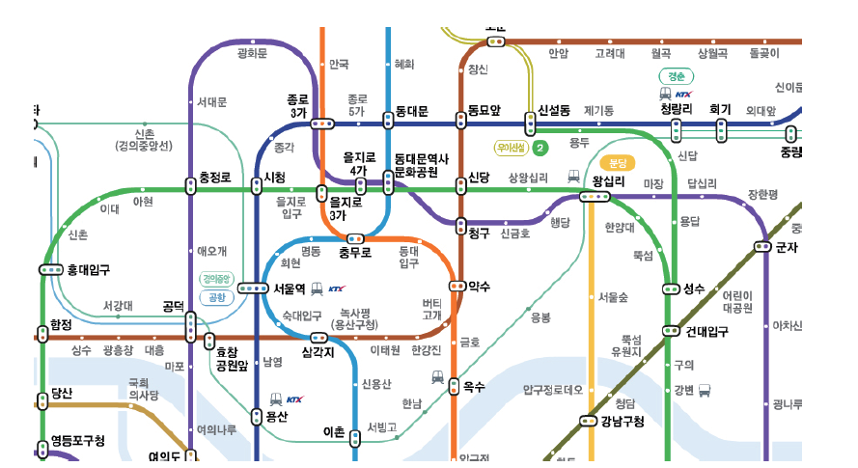
그래프의 예 : 서울 지하철 노선의 모습

그래프는 연결되어 있는 객체 간의 관계를 표현하는 자료구조 이다.

인접 행렬이나 인접 리스트로 메모리에 표현되고 처리됨.

ex) 전기 회로의 소자 간 연결 상태 지도에서 도시들의 연결 상태 트리(Tree)도 그래프의 특수한 경우이다.

그래프의 역사

Konigsberg의 다리 문제

1800년대 수학자 오일러(Euler)에 의해 창안.

오일러 문제

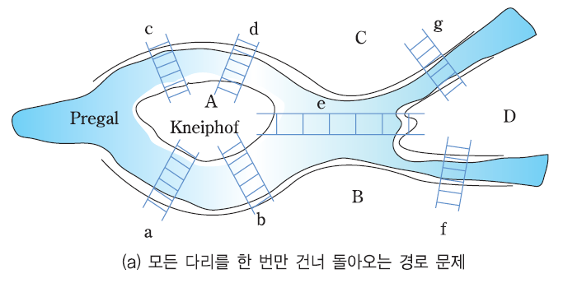
모든 다리를 한번만 건너서 처음 출발했던 장소로 돌아오는 문제.

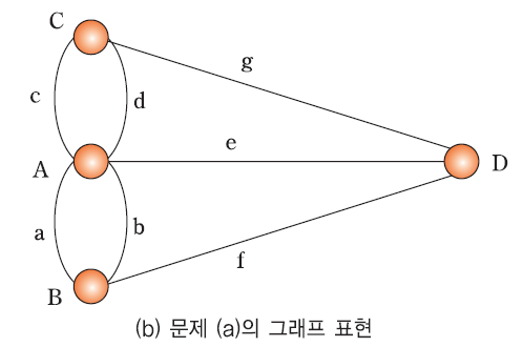
Konigsberg의 다리 문제 그래프 화

A, B, C, D 지역의 연결 관계 표현

위치: 정점(node)

다리: 간선(edge)

오일러 정리 (오일러 경로: 모든 간선을 한번만 통과하면서 처음 정점으로 돌아오는 경로)

모든 정점에 연결된 간선의 수가 짝수이면, 오일러 경로 존재.

따라서 그래프 (b)에는 오일러 경로가 존재하지 않는다.

그래프(graph) 의 정의

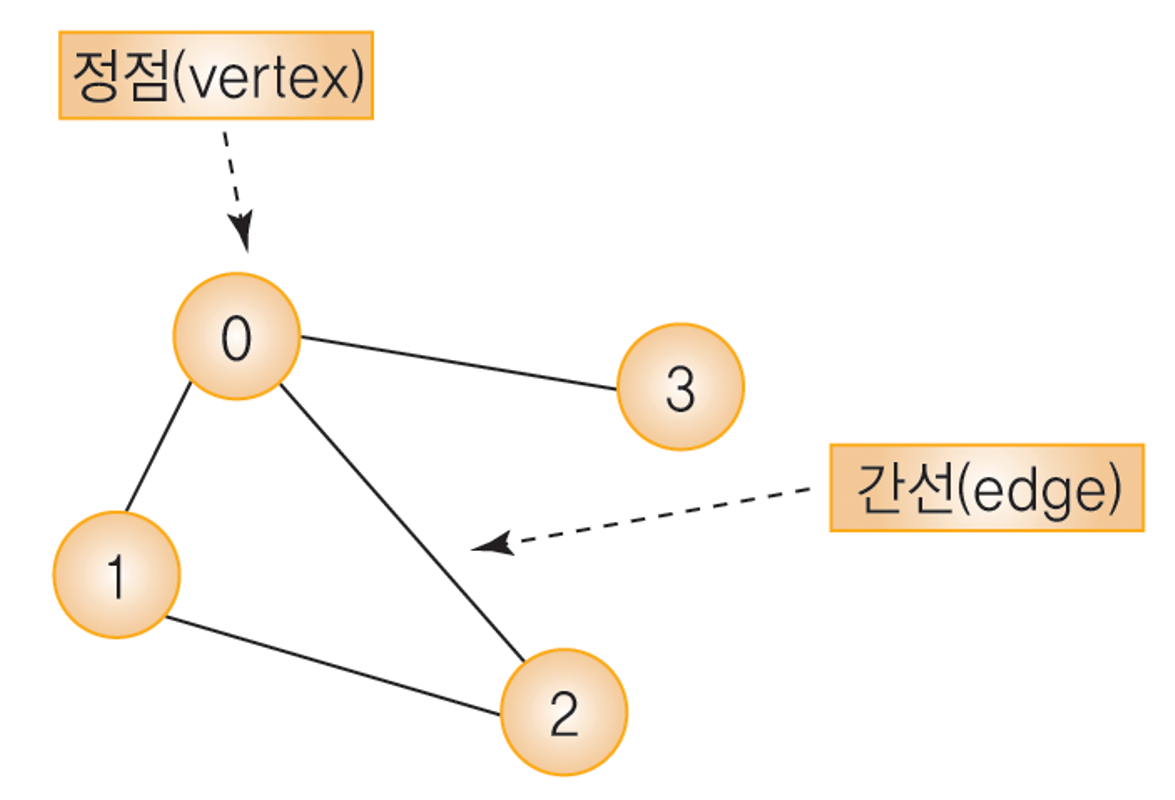
정점(vertex) 과 간선(edge)

정점(Vertex) 과 간선(Edge) 들의 유한 집합이라 할 수 있다.

그래프 G는 (V, E)로 표시.

정점(Vertex)

여러가지 특성을 가질 수 있는 객체를 의미한다.

V(G): 그래프 G의 정점들의 집합.

노드(node)라고도 불린다.

간선(edge)

정점들 간의 관계를 의미.

E(G): 그래프 G의 간선들의 집합

링크(link)라고도 불린다.

그래프 표현

그래프 표현의 예

그래프는 다음과 같이 집합의 형태로 표현될 수 있다.

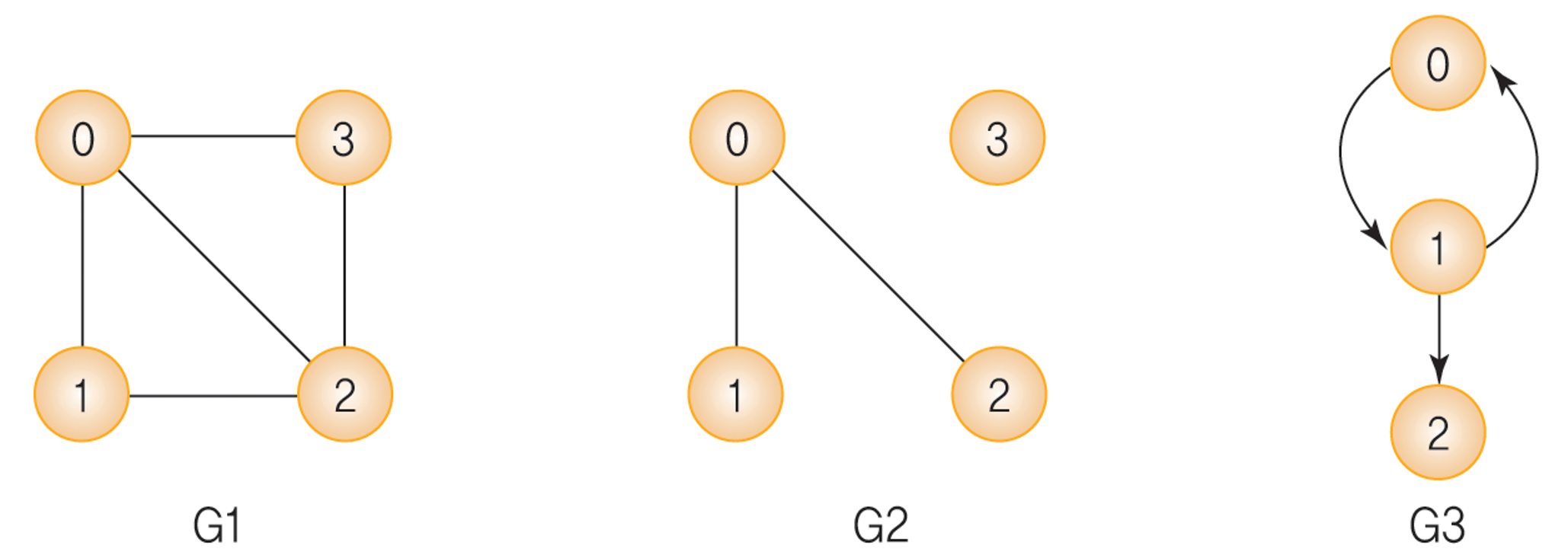
무방향 그래프 : () 안에 정점을 표시.

방향이 없으므로 괄호 안 정점의 순서가 바뀌어도 같은 간선이다.

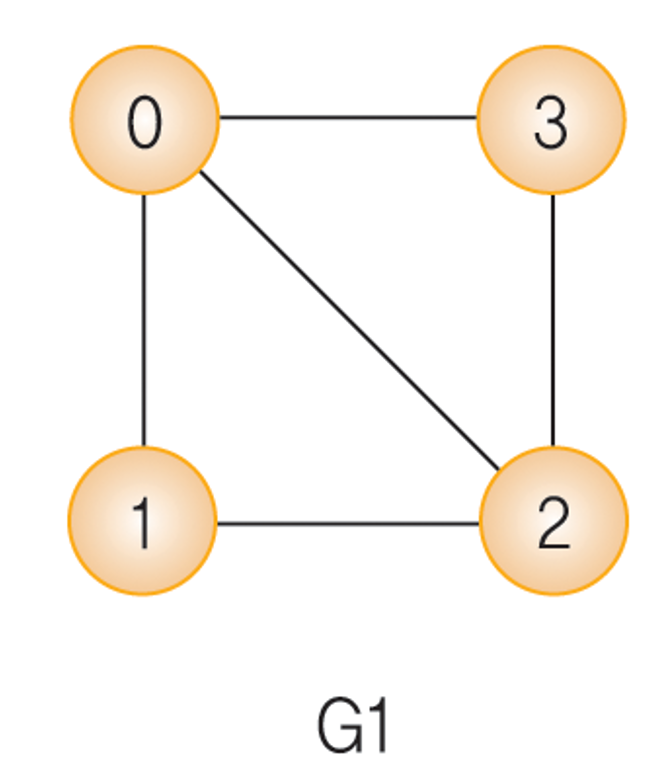
V(G1) = {0, 1, 2, 3}, E(G1) = {(0, 1), (0, 2), (0, 3), (1, 2), (2, 3)}

V(G2) = {0, 1, 2, 3}, E(G2) = {(0, 1), (0,2)}

방향 그래프: <> 안에 정점을 표시.

방향(–>)이 있으므로 괄호 안 정점의 순서가 다르면 다른 간선이다.

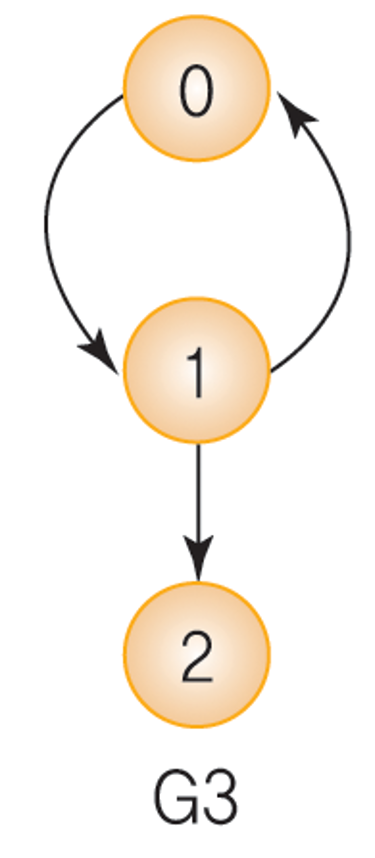
V(G3) = {0, 1, 2}, E(G3) = {<0, 1>, <1, 0>, <1, 2>}

무방향 그래프와 방향 그래프

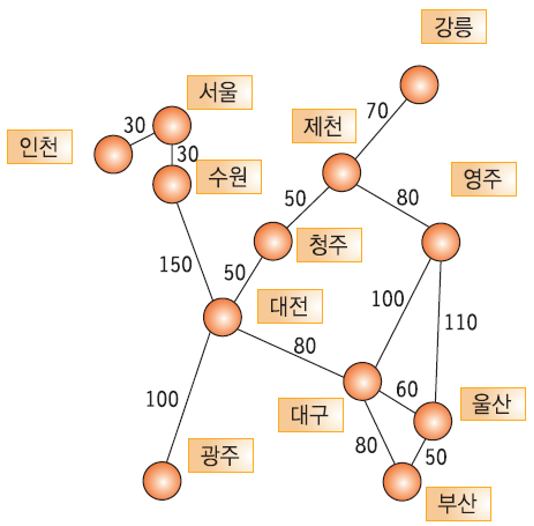
네트워크(가중치 그래프):

그래프의 간선에 가중치(weight)를 할당하여 두 정점간의 연결 유무 뿐만 아니라 연결 강도까지 나타낸 그래프

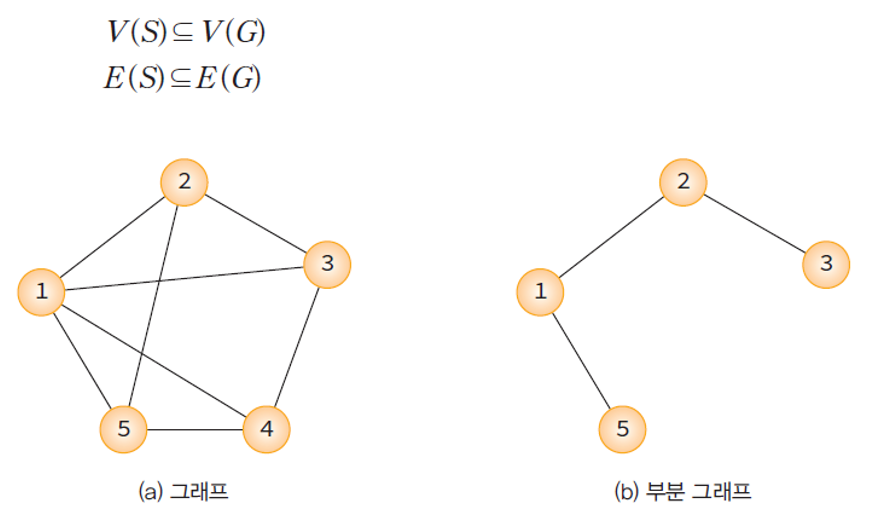
가중치 그래프(네트워크)의 예 - 지도

부분 그래프(sub graph):

어떤 그래프의 정점의 일부와 간선의 일부로 이루어진 그래프.

부분 그래프의 예 - 지도

정점의 차수:

인접 정점(adjacent vertex): 하나의 정점에서 간선에 의해 직접 연결된 정점.

무방향 그래프의 차수(degree):

하나의 정점에 연결된 다른 정점의 수.
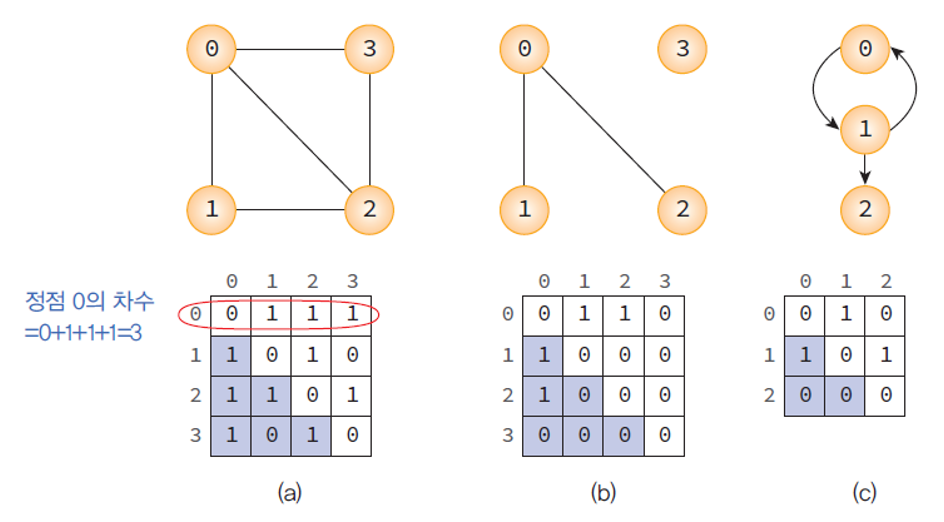
무방향 그래프의 차수

G1 에서 정점 0의 인접 정점: 정점 1, 정점 2, 정점 3

G1 에서 정점 0의 차수: 3

방향 그래프의 차수(degree):

방향 그래프의 차수

진입 차수(in-degree): 외부에서 오는 간선의 수

진출 차수(out-degree): 외부로 향하는 간선의 수

G3에서 정점 1의 차수:

내차수: 1, 외차수: 2

방향 그래프의 모든 진입(진출) 차수의 합은 간선의 수.

G3의 진입 차수의 합: 3

G3의 진출 차수의 합: 3

G3의 간선 합: 3

그래프의 경로(path)

무방향 그래프의 정점 s로부터 정점 e까지의 경로

정점의 나열(s, v1,v2,v3 .. e)로서, 나열된 정점들 간에는 반드시 간선(s, v1), (v1, v2), .. 가 있어야 한다.
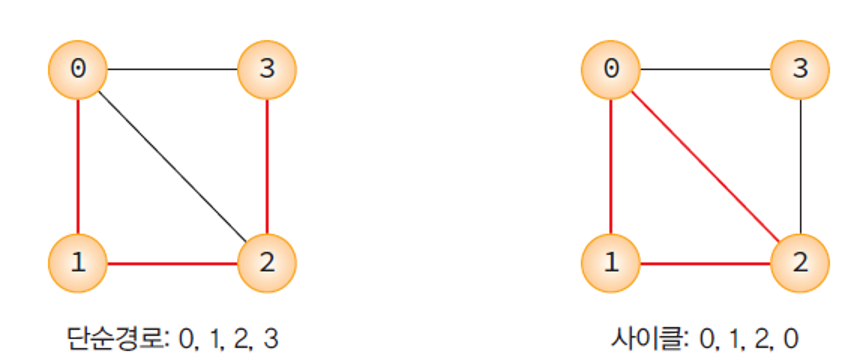
(방향 그래프: <s, v1>, <v1, v2> ..)

단순 경로(simple path)

경로 중에서 반복되는 간선이 없는 경로.

사이클(cycle)

단순 경로의 시작 정점과 종료 정점이 동일한 경로

예)

그래프의 경로 예

G1의 0,1,2,3은 경로지만, 0,1,3,2 는 경로가 아님.

G1의 1,0,2,3은 단순 경로이지만 1,0,2,0은 단순 경로가 아니다.

G1의 0,1,2,0과 G3의 0,1,0은 사이클.

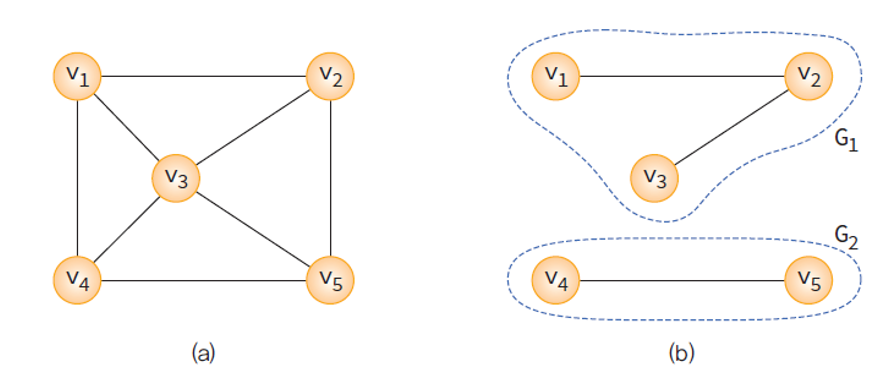
연결 그래프(connected graph):

연결 그래프

무방향 그래프 G에 있는 모든 정점쌍에대하여 항상 경로가 존재. (a)

(b)는 비연결 그래프 이다.

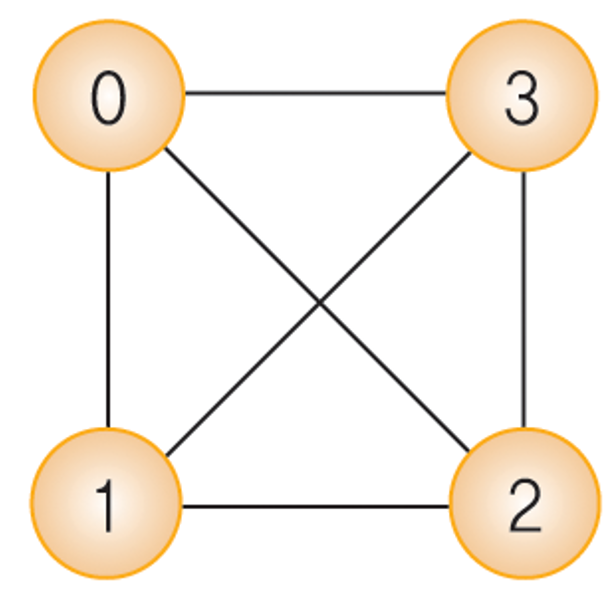
완전 그래프(complete graph):

모든 정점이 연결되어 있는 그래프

n개의 정점을 가진 무방향 완전 그래프의 간선의 수: n X (n-1) / 2

n = 4, 간선의 수 = (4X3) / 2 = 6

완전 그래프

그래프 ADT

정점의 집합과 간선의 집합
연산:

create_graph() // 그래프를 생성.

init(g) // 그래프 g 를 초기화 한다.

insert_vertex(g, v) // 그래프 g에 정점 v를 삽입한다.

insert_edge(g, u, v) // 그래프 g에 간선 (u, v) 를 삽입한다.

delete_vertex(g, v) // 그래프 g의 정점 v를 삭제한다.

delete_edge(g, u, v) // 그래프 g의 간선 (u, v) 를 삭제한다.

is_empty(g) // 그래프 g가 공백 상태인지 확인한다.

adjacent(v) // 정점 v에 인접한 정점들의 리스트를 반환한다.

destroy_graph(g) // 그래프 g를 제거한다.

그래프의 표현 방법

인접 행렬 (adjacent matrix) : 2차원 배열을 사용하여 그래프를 표현한다.

인접 리스트 (adjacent list) : 연결 리스트를 사용하는 그래프를 표현한다.

인접 행렬:

그래프의 정점 수 : n

n x n 의 2차원 행렬 M의 각원소를 다음의 규칙에 의해 할당.

if (간선(i, j) 가 그래프에 존재) : M[i][j] = 1;

else : M[i][j] = 0;

그래프의 표현 방법 - 인접 행렬

자체 간선 - (0,0), (1,1), (2,2)… 를 허용하지 않으므로 인접 행렬의 대각선 성분은 모두 0으로 표시된다.

n개의 정점을 가지는 그래프를 인접행렬로 표현하기 위해서는
간선의 수와 무관하게 항상 n^2개의 메모리 공간이 필요하다.

따라서 인접행렬은 그래프에 간선이 많이 존재하는 밀집 그래프(dense graph)를 표현하는 경우에 적합하다.

방향 그래프의 인접 행렬은 일반적으로 대칭이 아니다.

무방향 그래프의 인접 행렬은 대칭 행렬이 된다.

배열의 상위 삼각이나 하위 삼각만 저장하면 메모리를 절약 할 수 있다.

인접 행렬을 이용하면 두 정점을 연결하는 간선의 존재 여부를 O(1)시간 안에 즉시 알 수 있는 장점이 있다.

정점의 차수는 인접 행렬의 행 or 열을 조사하면 알 수 있으므로 O(n)의 연산에 의해 알 수 있다.

그래프에 존재하는 모든 간선의 수를 알아내려면 인접행렬 전체를 조사해야 하므로 n^2 번의 조사가 필요. O(n^2)

인접 행렬을 이용한 그래프 ADT의 구현
// 인접 행렬을 이용한 그래프 ADT의 구현

#include<stdio.h>
#include<stdlib.h>

#define MAX_VERTICES 50

typedef struct GraphType {
  int n; //정점의 개수
  int adj_mat[MAX_VERTICES][MAX_VERTICES];
}GraphType;

// 그래프 초기화
void init_graph(GraphType* g){
  int r, c;
  g->n = 0;

  for(r = 0; r < MAX_VERTICES; r++){
      for(c = 0; c < MAX_VERTICES; c++){
          g->adj_mat[r][c] = 0;
      }
  }
}

// 정점 삽입 연산
void insert_vertex(GraphType* g, int v){
  // 그래프의 정점 개수 + 1이 정의된 MAX_VERTICES 보다 크면 오류
  if(((g->n) + 1) > MAX_VERTICES) {
      fprintf(stderr, "그래프: 정점의 개수 초과\n");
      return;
  }
  // 정점 추가는 n만 증가시켜주면 된다. (현 예는 정적 배열이므로)
  g->n++;
}

// 간선 삽입 연산
void insert_edge(GraphType* g, int start, int end){
  if(start >= g->n || end >= g->n){
      fprintf(stderr, "그래프: 정점 번호 오류\n");
      return;
  }
  g->adj_mat[start][end] = 1;
  g->adj_mat[end][start] = 1;
  }

// 인접행렬 출력 함수
void print_adj_mat(GraphType* g){
  for(int i = 0; i < g->n; i++){
      for(int j = 0; j < g->n; j++){
          printf("%2d ", g->adj_mat[i][j]);
      }
      printf("\n");
  }
}

int main(){
 GraphType *g;
 g = (GraphType *)malloc(sizeof(GraphType));

 init_graph(g);

 for(int i=0;i<4;i++){
	   insert_vertex(g, i);
 }

 insert_edge(g, 0, 1);
 insert_edge(g, 0, 2);
 insert_edge(g, 0, 3);
 insert_edge(g, 1, 2);
 insert_edge(g, 2, 3);
 print_adj_mat(g);

 free(g);
}
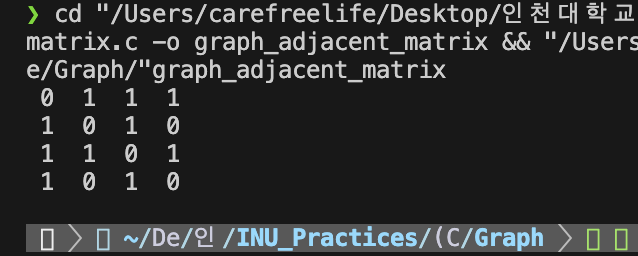
인접 행렬로 그래프 구현하기 - 실행 결과

인접 리스트로 표현된 그래프

각각의 정점에 인접한 정점들을 연결리스트로 표시한 것.

각 연결 리스트의 노드들은 인접 정점을 저장.

각 연결 리스트들은 하나의 배열로 구성된 헤더 노드를 가지고 있다.

따라서, 정점의 번호만 알면 해당 번호를 인덱스로 하여 각 정점의 연결 리스트에 쉽게 접근이 가능.

인접 리스트의 각각의 연결 리스트에 정점이 입력되는 순서에 따라
연결 리스트 내에서 정점들의 순서가 달라질 수 있다.

인접 리스트가 정점의 오름차 순으로 연결되도록 구현.

정점의 수가 n 개이고 간선의 수가 e 개인 무방향 그래프를 구현하기 위해서 필요한 것

n개의 연결리스트

n개의 헤더 노드

2e 개의 노드

인접 리스트는 간선의 개수가 적은 희소 그래프 (sparse graph)의 표현에 적합.

인접 리스트를 이용한 그래프 ADT의 구현
#include<stdio.h>
#include<stdlib.h>

#define MAX_VERTICES 50

typedef struct GraphNode{
int vertex;
struct GraphNode* link;
}GraphNode;

typedef struct GraphType {
int n; // 정점의 개수
GraphNode* adj_list[MAX_VERTICES]; // 인접 리스트
}GraphType;

// 그래프 초기화
void init_graph(GraphType* g){
  int v;
  g->n = 0;
  // 인접 리스트 초기화
  for(v = 0; v < MAX_VERTICES; v++){
      g->adj_list[v] = NULL;
  }
}

// 정점 삽입 연산 (행렬과 같음)
void insert_vertex(GraphType* g, int v){
  if(((g->n) + 1) > MAX_VERTICES) {
      fprintf(stderr, "그래프: 정점의 개수 초과\n");
      return;
  }
  g->n++;
}

// 간선 삽입 연산, v를 u의 인접리스트에 삽입한다.
// 정점 u에 간선 (u, v)를 삽입하는 연산은
// 정점 u의 인접 리스트에 간선을 나타내는 노드를 하나 생성하여 삽입하면 된다.
// 위치는 상관이 없으므로 삽입을 쉽게하기 위해 연결리스트의 처음에 삽입.
void insert_edge(GraphType* g, int u, int v){
  GraphNode* node;
  if(u >= g->n || v >= g->n){
      fprintf(stderr, "그래프: 정점 번호 오류\n");
      return;
  }
  node = (GraphNode*)malloc(sizeof(GraphNode));
  node->vertex = v;
  node->link = g->adj_list[u];
  g->adj_list[u] = node;
}

// 인접 리스트로 구현된 그래프 출력 함수.
void print_adj_list(GraphType* g){
  for(int i = 0; i < g->n; i++){
      GraphNode* p = g->adj_list[i];
      printf("정점 %d의 인접 리스트 ", i);
      while (p != NULL){
          printf("-> %d ", p->vertex);
          p = p->link;
      }
  printf("\n");        
  }
}

int main(void){
  GraphType* g;
  g = (GraphType*)malloc(sizeof(GraphType));
  init_graph(g);
  for(int i = 0; i < 4; i++){
      insert_vertex(g, i);
  }
  insert_edge(g, 0 ,1);
  insert_edge(g, 1 ,0);
  insert_edge(g, 0 ,2);
  insert_edge(g, 2 ,0);
  insert_edge(g, 0 ,3);
  insert_edge(g, 3 ,0);
  insert_edge(g, 1 ,2);
  insert_edge(g, 2 ,1);
  insert_edge(g, 2 ,3);
  insert_edge(g, 3 ,2);
  print_adj_list(g);
  free(g);
  return 0;
}
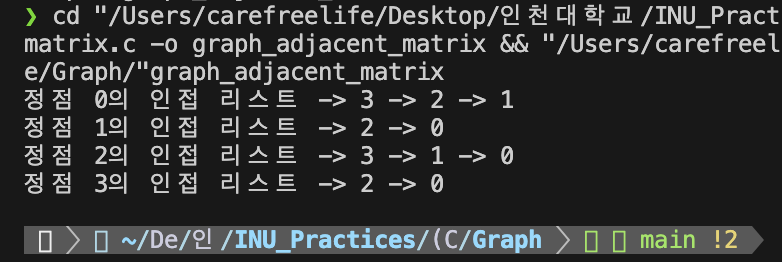
인접 리스트로 그래프 구현하기 - 실행 결과

그래프 탐색 - 깊이 우선 탐색(DFS: Depth First Search)

그래프 탐색의 두 가지 원리

그래프의 탐색?

하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한번씩 방문

많은 문제들이 단순히 그래프의 노드를 탐색하는 것으로 해결.

ex) 도로망을 사용해 특정 도시에서 다른 도시로 갈 수 있는지 여부. 전자회로에서 특정 단자와 다른 단자가 서로 연결되어 있는지 여부.

깊이 우선 탐색

한 방향으로 갈 수 있을 때까지 가다가 더 이상 갈 수 없게 되면 가장 가까운 갈림길로 돌아가
해당 위치에서부터 다른 방향으로 다시 탐색.

되돌아가기 위해서는 스택이 필요(순환 함수 호출로서 묵시적인 스택 이용 가능.)
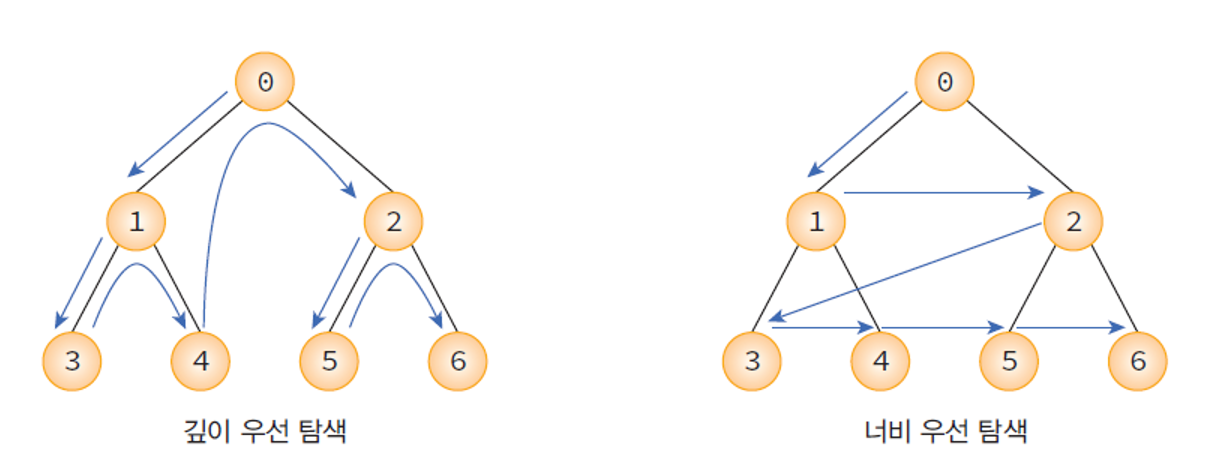
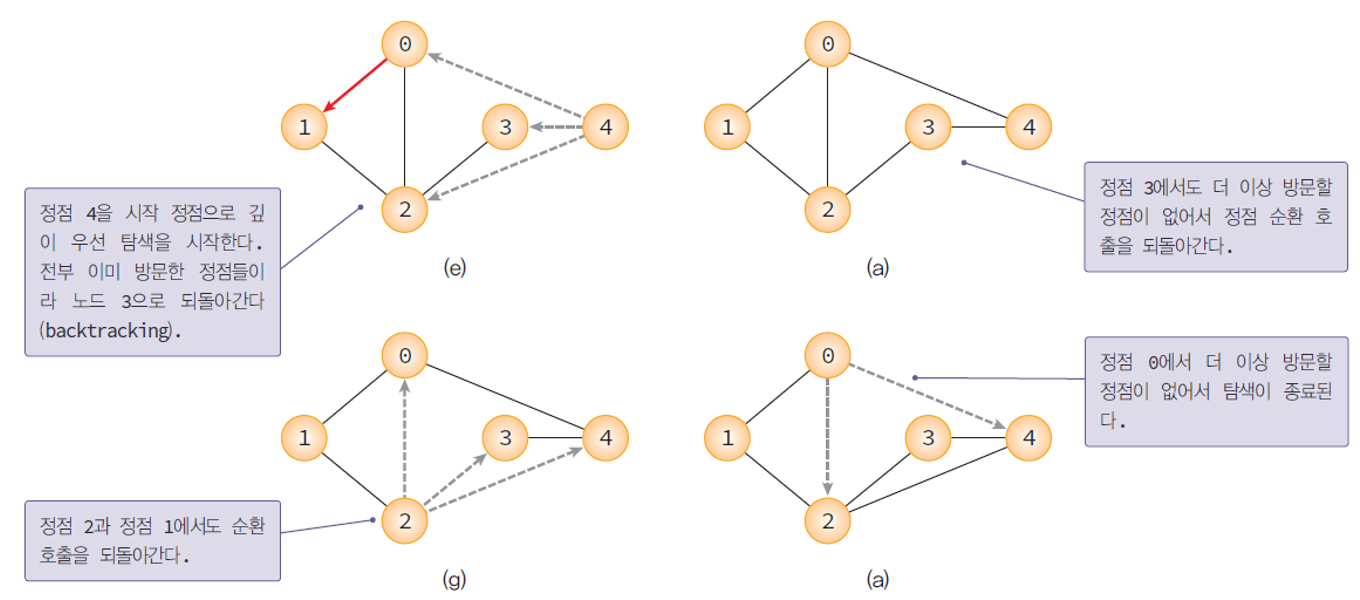
깊이 우선 탐색의 예

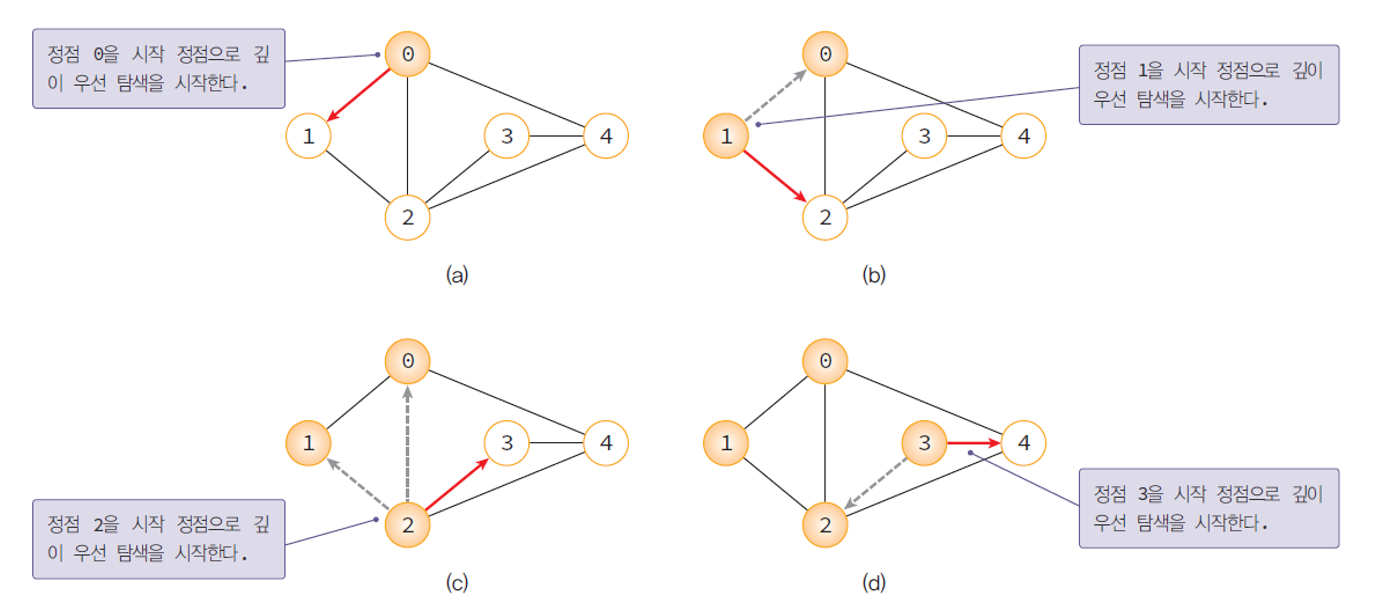
깊이 우선 탐색 알고리즘

DFS - 인접행렬 사용

// 깊이 우선 탐색 알고리즘 구현 - 인접 행렬 사용
// DFS Algorithm_adj_mat
int visited[MAX_VERTICES];
void dfs_mat(GraphType_mat* g, int v){
    int w;
    visited[v] = TRUE; // 정점 v의 방문 표시
    printf("정점 %d -> ", v); // 방문한 정점 출력
    for(w = 0; w < g->n; w++){
        if(g->adj_mat[v][w] && !visited[w]){
            dfs_mat(g, w); // 정점 w에서 DFS 새로 시작.
        }
    }
}

int main(){
    GraphType_mat *g;
    g = (GraphType_mat *)malloc(sizeof(GraphType_mat));

    init_graph(g);
    for(int i=0;i<4;i++){
        insert_vertex(g, i);
    }

    insert_edge(g, 0, 1);
    insert_edge(g, 0, 2);
    insert_edge(g, 0, 3);
    insert_edge(g, 1, 2);
    insert_edge(g, 2, 3);
    printf("깊이 우선 탐색\n");
    dfs_mat(g, 0);
    printf("\n");
    free(g);
    return 0;
}

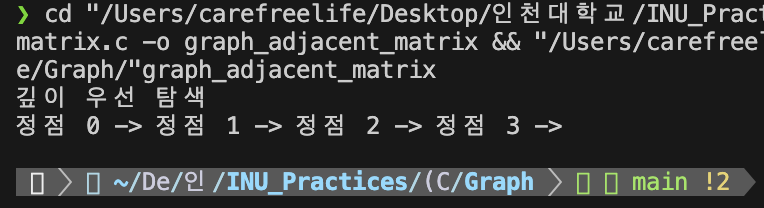
깊이 우선 탐색 알고리즘 결과

DFS - 인접리스트 사용

int visited[MAX_VERTICES];

// 인접 리스트로 표현된 그래프에 대한 깊이 우선 탐색
void dfs_list(GraphType* g, int v){
    GraphNode* w;
    visited[v] = TRUE; // 정점 v의 방문 표시
    printf("정점 %d -> ", v); //방문한 정점 출력
    for(w = g->adj_list[v]; w; w = w->link){    // 인접 정점 탐색
        // 만약 인접 정점 중 방문하지 않은 노드가 있다면
        if(!visited[w->vertex]){
            dfs_list(g, w->vertex); //정점 w에서 dfs 새로 시작.
        }
    }
}

깊이 우선 탐색(DFS)의 분석

깊이 우선 탐색은 모든 간선을 조사.

정점의 수가 n이고 간선의 수가 e인 그래프

그래프가 인접 리스트로 표현되었을 때 시간 복잡도 : O(n + e)

그래프가 인접 행렬로 표현 되었을 때 시간 복잡도 : O(n^2)

희소 그래프인 경우, 인접 리스트가 인접 행렬보다 유리.

그래프 탐색 - 너비 우선 탐색(BFS : Breath First Search)

너비 우선 탐색(Breath First Search : BFS)

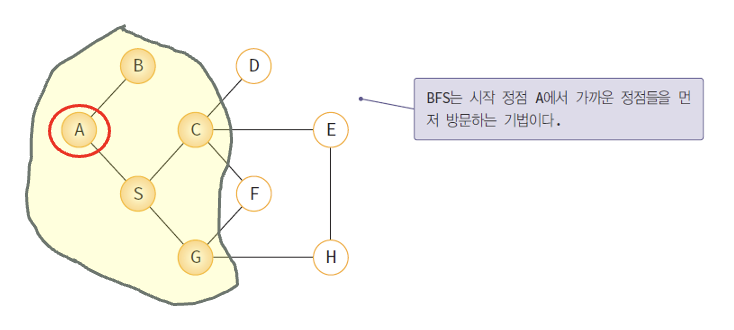
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법.  

너비 우선 탐색 (Breath First Search : BFS)

시작 정점 A를 방문한다.

정점 A의 인접 정점인 {B, S}를 차례대로 방문한다.

정점 {B, S}의 인접 정점인 {C, G}를 방문한다.

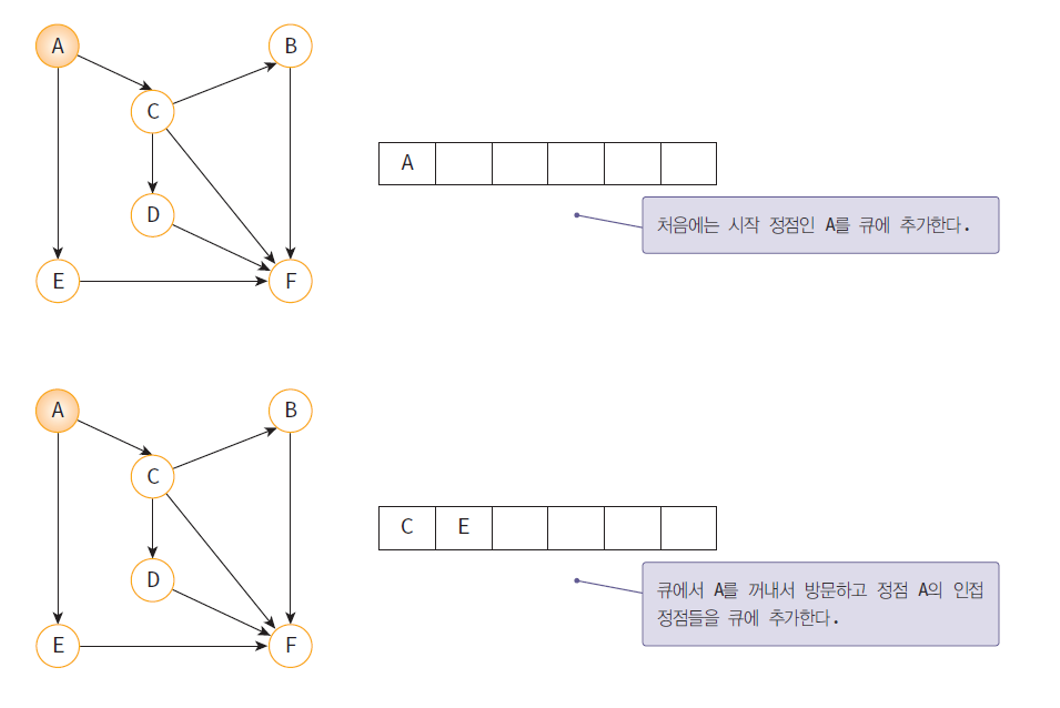
너비 우선 탐색에서는 인접 정점을 차례대로 저장 후 꺼낼 수 있는 큐(Queue)가 필요하다.

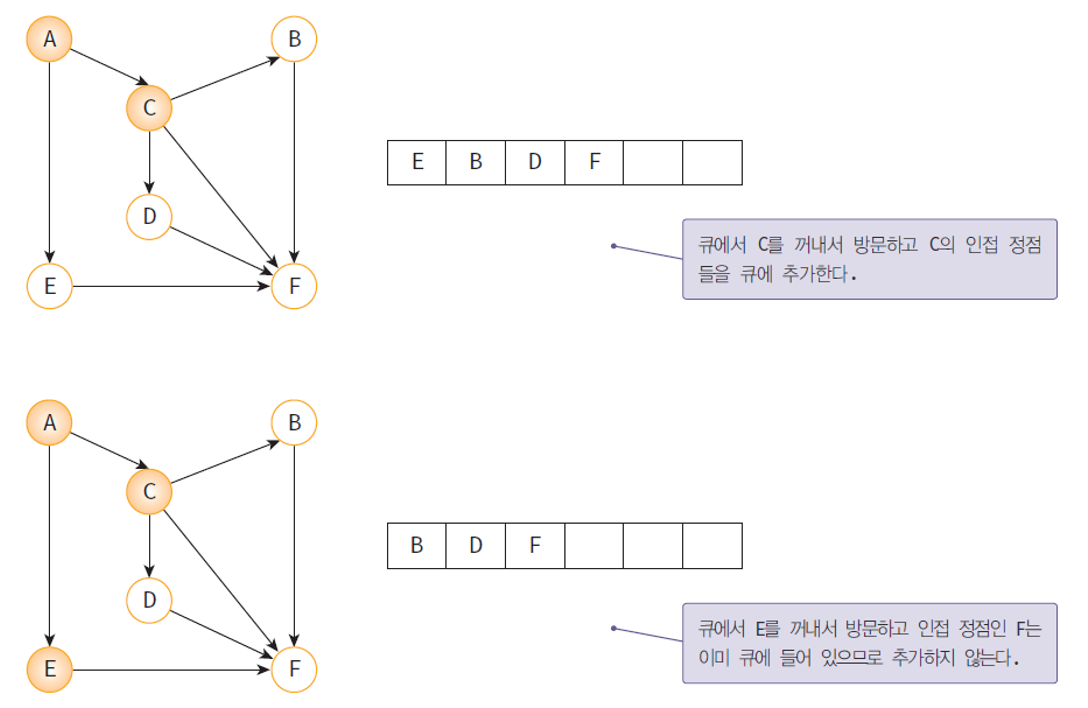
큐에 저장된 정점을 꺼내 방문 후

해당 정점의 인접 정점을 차례대로 큐에 넣는다.

위 과정을 큐가 소진 될 때까지 반복한다.

너비 우선 탐색 알고리즘 1

너비 우선 탐색 알고리즘 2

너비 우선 탐색의 특징: 시작 정점으로부터 거리가 가까운 정점의 순서로 탐색을 진행한다.

거리가 d인 정점을 전부 방문 후, 거리가 (d+1)인 정점들을 모두 방문… 반복

거리가 1인 정점 -> 거리가 2인 정점 -> 거리가 3인 정점… 과 같은 순서로 정점들을 방문해 나간다.

너비 우선 탐색(BFS) 의 구현

너비 우선 탐색 - 인접 행렬 및 인접 리스트 사용

#include<stdio.h>
#include<stdlib.h>

#define TRUE 1
#define FALSE 0
#define MAX_QUEUE_SIZE 10
#define MAX_VERTICES 50

typedef int element;

typedef struct {
    element queue[MAX_QUEUE_SIZE];
    int front, rear;
} QueueType;

// 오류 함수
void error(char *message){
    fprintf(stderr, "%s", message);
    exit(1);
}

// 큐 초기화
void queue_init(QueueType *q){
    q->front = q->rear = 0;
}

// 공백 상태 검출 함수
int is_empty(QueueType *q){
    return q->front == q->rear;
}

// 포화 상태 검출 함수
int is_full(QueueType *q){
    return ((q->rear + 1) % MAX_QUEUE_SIZE == q->front);
}

// 삽입 함수
void enqueue(QueueType *q, element item){
    if(is_full(q)){
        error("큐: 포화 상태\n");
    }
    q->rear = (q->rear + 1) % MAX_QUEUE_SIZE;
    q->queue[q->rear] = item;
}

// 삭제 함수.
element dequeue(QueueType *q){
    if(is_empty(q)){
        error("큐: 공백 상태\n");
        exit(1);
    }
    q->front = ((q->front - 1) % MAX_QUEUE_SIZE);
    return q->queue[q->front];
}

////////////////// 인접 행렬로 구현된 너비 우선 탐색 //////////////////

typedef struct GraphType{
    int n;
    int adj_mat[MAX_VERTICES][MAX_VERTICES];
}GraphType;

int visited[MAX_VERTICES];

// 그래프 초기화
void init_graph(GraphType *g){
    int r, c;
    g->n = 0;
    for(r = 0; r < MAX_VERTICES; r++){
        for(c = 0; c < MAX_VERTICES; c++){
            g->adj_mat[r][c] = 0;
        }
    }
}

// 정점 삽입 연산
void insert_vertex(GraphType *g, int v){
    if((g->n) + 1 > MAX_VERTICES){
        fprintf(stderr, "정점 개수 초과\n");
        return;
    }
    g->n++; // 정점의 삽입은 정점 개수의 증가로서만 구현된다.
}

// 간선 삽입 연산
void insert_edge(GraphType *g, int start, int end){
    // 간선의 양 정점 번호가 최대 정점 개수보다 크면 오류.
    if(start >= g->n || end >= g->n){
        fprintf(stderr, "간선을 잇는 정점의 번호 오류\n");
        return;
    }
    // 인접 행렬으로 구현된 그래프이므로 양방향 전부 간선이 있음을 표시해 주어야 한다.
    g->adj_mat[start][end] = 1;
    g->adj_mat[end][start] = 1;
}

void bfs_mat(GraphType* g, int v){
    
    printf("ok");
    QueueType *q = (QueueType *)malloc(sizeof(QueueType));
    queue_init(q);  // 큐 초기화
    visited[v] = TRUE;  // 시작 정점 v의 방문 표시.
    printf("%d 방문 -> ", v);
    enqueue(q, v);  // 시작 정점을 큐에 저장.
    
    // 큐가 공백 상태가 될 때까지 반복.
    while(!is_empty(q)){
        v = dequeue(q); // 큐에서 정점을 추출.
        // 인접 정점 탐색
        for(int w = 0; w < g->n; w++){
            // 시작 정점 v와 이어진 간선의 반대 정점 w가 있고(1로 나타내어짐),
            // visited 배열에 해당 정점 w가 존재하지 않는다면
            if(g->adj_mat[v][w] && !visited[w]){
                visited[w] = TRUE; // 정점 w의 방문 표시.
                printf("%d 방문 -> ", w);
                enqueue(q,w); // v의 인접 정점인 w를 큐에 삽입.
            }
        }
    }
    free(q);
}

////////////////// 인접 리스트로 구현된 너비 우선 탐색 //////////////////

typedef struct GraphNode {
    int vertex;
    struct GraphNode *link;
}GraphNode;

typedef struct GraphType_adj_list {
    int n;
    GraphNode *adj_list[MAX_VERTICES];
}GraphType_adj_list;

void init_graph_adj_list(GraphType_adj_list *g){
    g->n = 0;
    for(int i = 0; i < MAX_VERTICES; i++){
        g->adj_list[i] = NULL;
    }
}

void insert_vertex_adj_list(GraphType_adj_list *g){
    if(((g->n) + 1) > MAX_VERTICES){
        fprintf(stderr, "정점의 개수 초과\n");
        return;
    }
    // 인접행렬로 구현된 BFS와 마찬가지로 정점의 삽입은 개수의 증가 뿐이다.
    g->n++;
}

void insert_edge_adj_list(GraphType_adj_list *g, int u, int v){
    GraphNode *node;
    if(u >= g->n || v >= g->n){
        fprintf(stderr, "정점의 번호가 정점의 개수와 불일치\n");
        return;
    }
    node = (GraphNode*)malloc(sizeof(GraphNode));
    node->vertex = v;
    node->link = g->adj_list[u];
    g->adj_list[u] = node;
}

void bfs_list(GraphType_adj_list* g, int v){
    GraphNode *w = (GraphNode*)malloc(sizeof(GraphNode));
    QueueType *q = (QueueType*)malloc(sizeof(QueueType));
    
    queue_init(q);    // 큐의 초기화
    visited[v] = TRUE;  //  첫번째 정점 v 방문 표시
    printf("%d 방문 -> ", v);
    enqueue(q, v);  // 시작 정점을 큐에 삽입
    while (!is_empty(q)){   // 큐가 소진 될 때까지 실행
        v = dequeue(q);
        // 정점의 인접 리스트 끝까지 탐색.
        for(w = g->adj_list[v]; w; w = w->link){
            // 정점의 인접 리스트 중 아직 방문하지 않은 정점이 있다면
            if(!visited[w->vertex]){
                visited[w->vertex] = TRUE;  // 해당 정점의 방문 표시
                printf("%d 방문 -> ", w->vertex);
                enqueue(q, w->vertex);  // 해당 정점을 큐에 삽입.
            }
        }
    }
    free(w);
    free(q);
}

int main(void)
{
    /////// 인접 행렬로 구현한 BFS ///////

	GraphType *g;
	g = (GraphType *)malloc(sizeof(GraphType));
	init_graph(g);
	for (int i = 0; i<6; i++)
		insert_vertex(g, i);
	insert_edge(g, 0, 2);
	insert_edge(g, 2, 1);
	insert_edge(g, 2, 3);
	insert_edge(g, 0, 4);
	insert_edge(g, 4, 5);
	insert_edge(g, 1, 5);

    /////// 인접 리스트로 구현한 BFS ///////

    GraphType_adj_list *g_adj_list 
    = (GraphType_adj_list*)malloc(sizeof(GraphType_adj_list));

    init_graph_adj_list(g_adj_list);

	for (int i = 0; i<6; i++)
		insert_vertex_adj_list(g_adj_list);
	insert_edge_adj_list(g_adj_list, 0, 2);
	insert_edge_adj_list(g_adj_list, 2, 1);
	insert_edge_adj_list(g_adj_list, 2, 3);
	insert_edge_adj_list(g_adj_list, 0, 4);
	insert_edge_adj_list(g_adj_list, 4, 5);
	insert_edge_adj_list(g_adj_list, 1, 5);

	printf("너비 우선 탐색 - 인접 행렬\n");
	bfs_mat(g, 0);
	printf("\n");

	printf("너비 우선 탐색 - 인접 리스트\n");
    bfs_list(g_adj_list, 0);
    printf("\n");

	free(g);
    free(g_adj_list);

	return 0;
}

너비 우선 탐색의 분석

너비 우선 탐색의 시간 복잡도:

인접 리스트 : 전체 수행 시간은 O(n + e)

인접 행렬 : 전체 수행 시간은 O(n^2)

너비 우선 탐색도 깊이 우선 탐색과 같이 희소 그래프인 경우 인접 리스트를 사용하는 것이 효율적.

최대한의 설명을 코드 블럭 내의 주석으로 달아 놓았습니다.

혹시 이해가 안가거나 추가적인 설명이 필요한 부분, 오류 등의 피드백은 언제든지 환영합니다!

긴 글 읽어주셔서 감사합니다. 포스팅을 마칩니다.

처음으로~

참고: C언어로 쉽게 풀어쓴 자료구조 <개정 3판> 천인국, 공용해, 하상국 지음

Task Lists

Twitter Facebook LinkedIn

Chae Seungmin

Data Structure - 그래프 (Graph) 란? (1)

그래프 (graph) 란?

그래프의 역사

그래프(graph) 의 정의

그래프 표현

그래프 ADT

그래프의 표현 방법

그래프 탐색 - 깊이 우선 탐색(DFS: Depth First Search)

깊이 우선 탐색(DFS)의 분석

그래프 탐색 - 너비 우선 탐색(BFS : Breath First Search)

너비 우선 탐색(BFS) 의 구현

너비 우선 탐색 - 인접 행렬 및 인접 리스트 사용

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)

※블로그 이전 안내※

Chae Seungmin

그래프 (graph) 란?

그래프의 역사

그래프(graph) 의 정의

그래프 표현

그래프 ADT

그래프의 표현 방법

그래프 탐색 - 깊이 우선 탐색(DFS: Depth First Search)

깊이 우선 탐색(DFS)의 분석

그래프 탐색 - 너비 우선 탐색(BFS : Breath First Search)

너비 우선 탐색(BFS) 의 구현

너비 우선 탐색 - 인접 행렬 및 인접 리스트 사용

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)