[Data Structure]
정렬(Sort)(1) - 선택 정렬(Selection Sort) / 삽입 정렬(Insertion Sort) / 버블 정렬(Bubble Sort)
정렬(Sorting) 이란?
정렬(sorting)은
어떠한 대상을 오름차순 (ascending order) 및 내림차순 (descending order) 으로 나열하는 것.
[출처](https://engoo.co.kr/app/lessons/sort-out-settle-for-count-on-fall-behind-do-over/_H6h7FHeEeetxgef8rkGgA)정렬 (Sorting)
- 정렬은 컴퓨터 공학에서 가장 기본적이고 중요한 알고리즘 중의 하나.
- 자료 탐색에 있어 필수적 - 탐색의 효율성 증대.
- 정렬시켜야 할 대상 : 레코드(record)
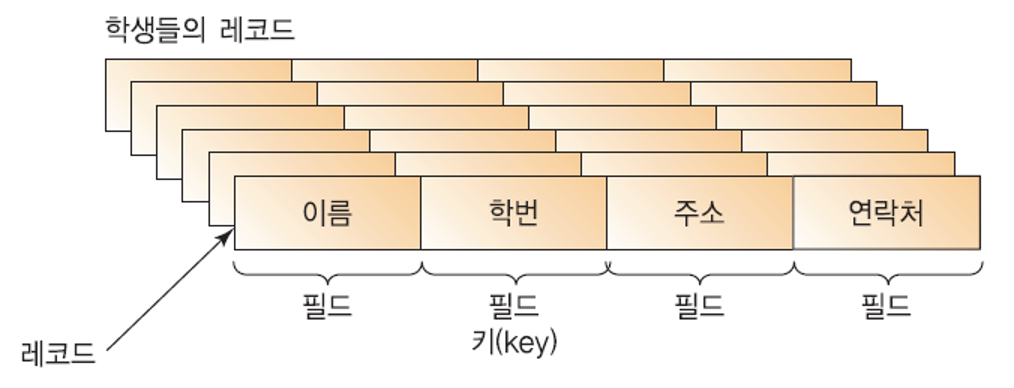
- record 내부의 요소 : 필드 (ex. 이름. 학번. 주소. 주민번호.)
- 레코드와 레코드를 식별해주는 역할을 하는 필드 : 키(key)
- 정렬이란: 레코드들을 key값의 순서로 재배열 하는 것.
레코드(record)와 필드의 모습.내부 정렬 (internal sorting):
- 모든 데이터가 주 기억장치 내부에 저장된 상태에서 정렬.
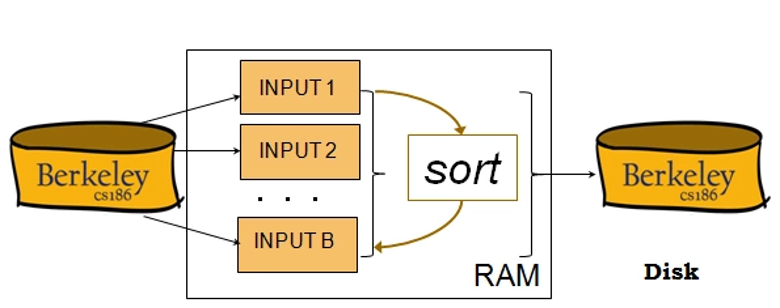
외부 정렬 (external sorting):
- 외부 기억 장치에 대부분의 데이터가 존재.
- 일부만 주 기억장치에 저장된 상태에서 정렬.
[출처](https://cs186.fandom.com/wiki/External_Sorting)내부 정렬과 외부 정렬의 모습정렬 알고리즘의 안정성 (Stability)
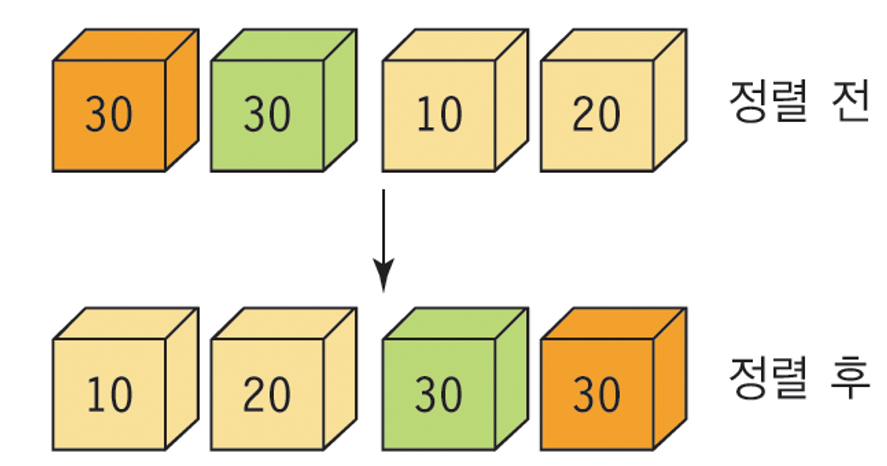
- 동일 한 키 값을 갖는 레코드들의 상대적인 위치가 정렬 후에도 같은 것.
- 안정하지 못한 정렬의 예
안정하지 못한 정렬
선택 정렬 (Selection Sort) 이란?
가장 기초적인 정렬
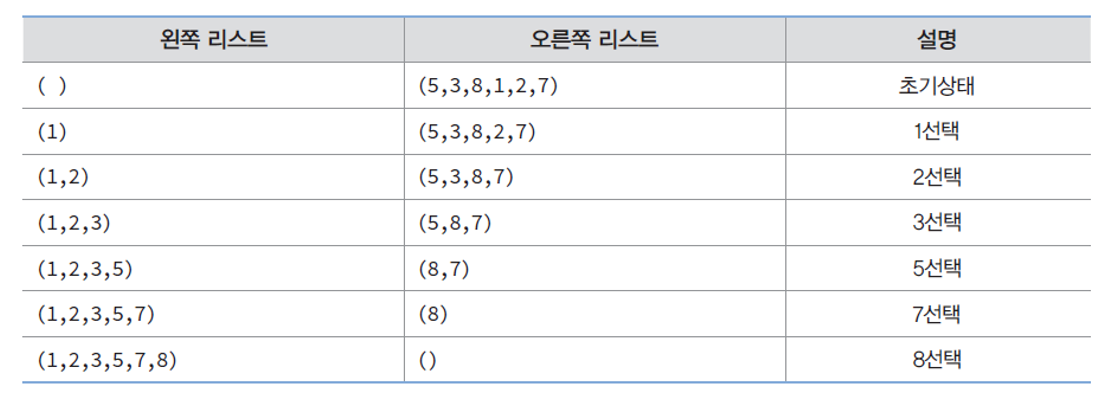
정렬된 왼쪽 리스트와 정렬되지 않은 오른쪽 리스트가 있다고 가정.
- 왼쪽 리스트는 비어 있고, 정렬할 숫자들은 모두 오른쪽 리스트에 존재.
- 오른쪽 리스트에서 가장 작은 숫자를 선택하여 왼쪽 리스트로 이동하는 작업을 되풀이.
- 오른쪽 리스트가 공백이 되면 종료.
선택 정렬(Selection Sort)하지만 위의 방법으로 정렬 진행 시, 정렬 대상이 입력된 배열과는 별개로 추가적인 배열 하나를 더 필요로 한다.
- 메모리 절약을 위해 제자리 정렬(in-place sorting)방법을 사용할 수 있다.
- 입력 배열에서 최소값을 발견하면 배열의 첫번째 요소와 교환.
- 두번째 최소값은 배열의 두번째 요소와 교환.
- 정렬 대상 요소의 개수 - 1 만큼 반복하면 제자리 정렬이 가능하다.
제자리 정렬(in-place Sort)의 과정
선택 정렬의 알고리즘
‼️주의‼️ i값은 0부터 n-2 까지만 변화한다.
list[0] 부터 list[n-2] 까지 정렬이 되었다면, 이미 list[n-1]이 가장 큰 값이기 때문에 정렬해 줄 필요가 없다!
// 선택 정렬 알고리즘 - pseudo code
selection_sort(A, n)
for i ← 0 to n-2 do
least ← A[i], A[i+1], ... , A[n-1] 중에서 가장 작은 값의 인덱스;
A[i]와 A[least]의 교환;
i++;
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define MAX_SIZE 10
// 레코드와 레코드의 교환을 위한 SWAP 매크로
#define SWAP(x, y, t) ((t) = (x), (x) = (y), (y) = (t))
int list[MAX_SIZE];
int n;
void selection_sort(int list[], int n){
int i, j, least, temp;
for(i = 0; i < n - 1; i++){ // n - 2 까지만 정렬!!
least = i;
// 리스트 내 최소값 탐색
for(j = i; j < n; j++){
if(list[j] < list[least]) least = j;
}
// 탐색하여 찾은 최소값과 현재 단계의 값을 교환.
SWAP(list[i], list[least], temp);
}
}
int main(void) {
int i;
n = MAX_SIZE;
srand(time(NULL));
for (i = 0; i<n; i++) // 난수 생성 및 출력
list[i] = rand() % 100; // 난수 발생 범위 0~99
selection_sort(list, n); // 선택정렬 호출
for (i = 0; i<n; i++)
printf("%d ", list[i]);
printf("\n");
return 0;
}
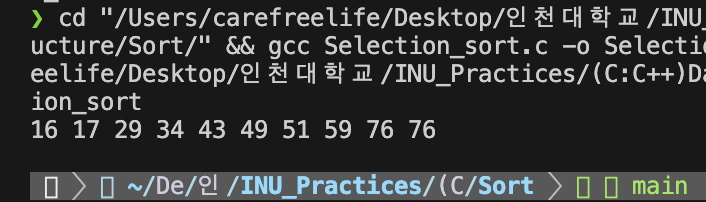
선택 정렬 알고리즘 실행 결과선택 정렬의 분석
- 비교 횟수: 두 개의 for문
- 외부 루프 : n-1 번
- 내부 루프 : 0 부터 n-2 까지 변하는 i에 대하여 (n-1)-i 번 반복.
- 전체 비교 횟수 : n(n-1)/2 = O(n^2)
- 이동 횟수: 레코드의 교환(SWAP)횟수는 외부 루프의 횟수와 같다.(n-1)
- 한번 교환하기 위하여 3번의 이동이 필요. (x->t, y->x, t->y) (*3)
- 전체 이동 횟수 : 3(n-1)
선택 정렬의 장점 : 자료 이동 횟수가 미리 결정된다
선택 정렬의 단점 : 안정성을 만족하지 않는다
이미 자료가 정렬된 경우에는 자기 자신과의 불필요한 이동을 하게 된다.
- 다음과 같은 if문을 추가해 문제를 개선할 수 있다.
// 만약 최소값이 자기 자신이면 이동하지 않는다. (SWAP 호출 X) if(i != least){ SWAP(list[i], list[least], temp); }
삽입 정렬(Insertion Sort) 의 원리
삽입 정렬(Insertion Sort)은 손 안의 카드를 정렬하는 방법과 유사하다.
: 정렬되어 있는 리스트에 새로운 레코드를 적절한 위치에 삽입하는 과정을 반복
카드를 잘 정렬해 두었다가 뽑아야 한다삽입 정렬의 과정
- 정렬되어 있지 않은 부분의 첫 번째 숫자가 정렬된 부분의 어느 위치에 삽입되어야 하는가?
- 적절한 위치에 해당 요소를 삽입
- 정렬되지 않은 부분의 크기 : -1
- 정렬된 부분의 크기 : +1
- 정렬되지 않은 부분이 빌 때까지 반복
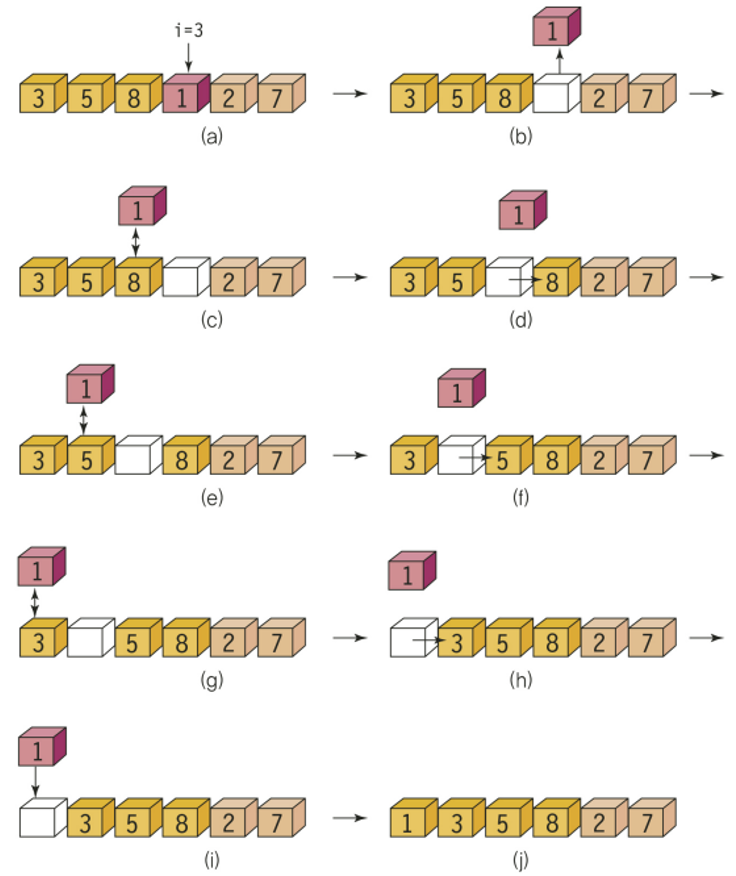
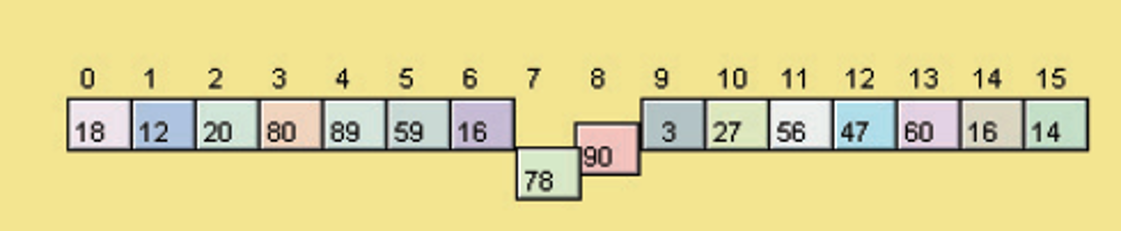
삽입 정렬의 과정
삽입 정렬의 알고리즘
// 삽입 정렬의 알고리즘 - pseudo code
insertion_sort(A, n):
for i ← 1 to n-1 do // 1. 인덱스 1부터 시작한다. 인덱스 0은 이미 정렬된 것으로 볼 수 있다.
key ← A[i]; // 2. 현재 삽입될 숫자인 i번째 정수를 key 변수로 복사
j ← i-1; // 3. 현재 정렬된 배열은 i-1 까지이므로 i-1 번째부터 역순으로 탐색.
while j >= 0 and A[j] > key do // 4. j값이 음수가 아니고, key값보다 정렬된 배열에 있는 값이 크면
A[j+1] ← A[j]; // 5. j번째 값을 j+1 번째로 이동.
j ← j-1; // 6. j 값을 하나 감소.
A[j+1] ← key // 7. j번째 정수가 key보다 작으므로 j+1번째에 key값이 삽입된다.
삽입 정렬의 과정
// 나머지 코드는 선택 정렬과 같다.
// 삽입 정렬
void insertion_sort(int list[], int n){
int i, j, key;
for(i = 1; i < n; i++){
key = list[i];
for(j = i - 1; j >= 0 && key < list[j]; j = j - 1){
list[j+1] = list[j]; // 레코드의 오른쪽 이동
}
// 내부 for문이 끝나면 list[j]는 key보다 작은 값.
// 따라서 key가 삽입될 곳은 list[j+1]이 된다.
list[j+1] = key;
}
}
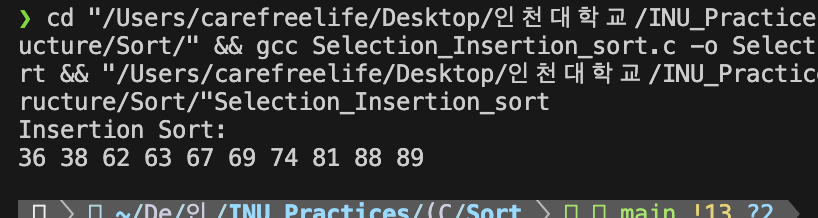
삽입 정렬 알고리즘 - 실행 결과삽입 정렬의 복잡도 분석
삽입 정렬의 복잡도는 입력 자료의 구성에 따라 다름.
- 외부 루프 : n-1 번 반복
- 각 단계마다 1번의 비교: j >= 0 && key < list[j]
- 각 단계마다 2번의 이동: list[j+1] = list[j];(레코드 오른쪽 이동)
- (최선)입력 자료가 정렬되어 있는 경우 : 가장 빠름 -> O(n)
- 비교 : n-1번
- 이동 : 0번
- 시간 복잡도 : O(n)
- (최악)역순으로 정렬되어 있는 경우 : O(n^2)
- 모든 단계에서 앞에 놓인 자료 전부 이동
- 비교 : n(n-1)/2 = O(n^2)
- 이동 : n(n-1)/2 + 2(n-1) = O(n^2)
- 평균의 경우 O(n^2)
- 많은 이동이 필요하므로 레코드가 클 경우 불리한 정렬 방법.
- 안정된 정렬 방법
- 대부분 정렬되어 있는 자료인 경우 매우 효율적
버블 정렬(Bubble Sort)의 원리
버블 정렬(Bubble Sort) : 인접한 두 개의 레코드를 비교하여 순서대로 되어 있지 않으면 서로 교환
버블 정렬의 모습버블 정렬: 인접한 두 개의 레코드를 비교하여 크기가 순서대로 되어있지 않으면 서로 교환하는 비교-교환 과정.
- 리스트의 왼쪽 끝에서 시작하여 오른쪽 끝까지 진행.
- 비교-교환 과정(스캔)이 한번 완료되면 가장 큰 record가 리스트의 오른쪽 끝에 위치.
- 비교-교환 과정은 정체 숫자가 전부 정렬될 때까지 반복.
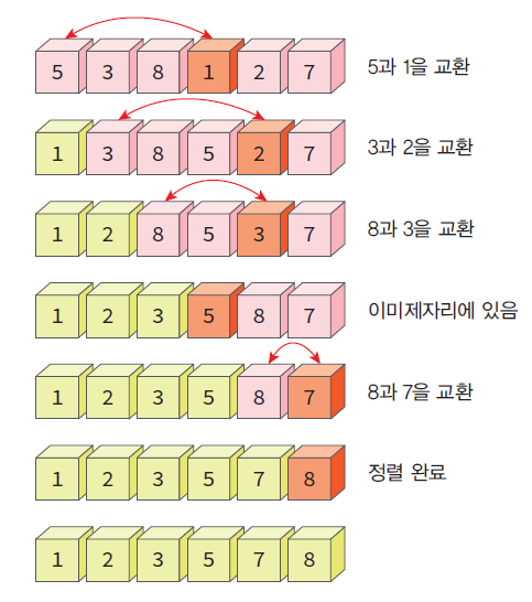
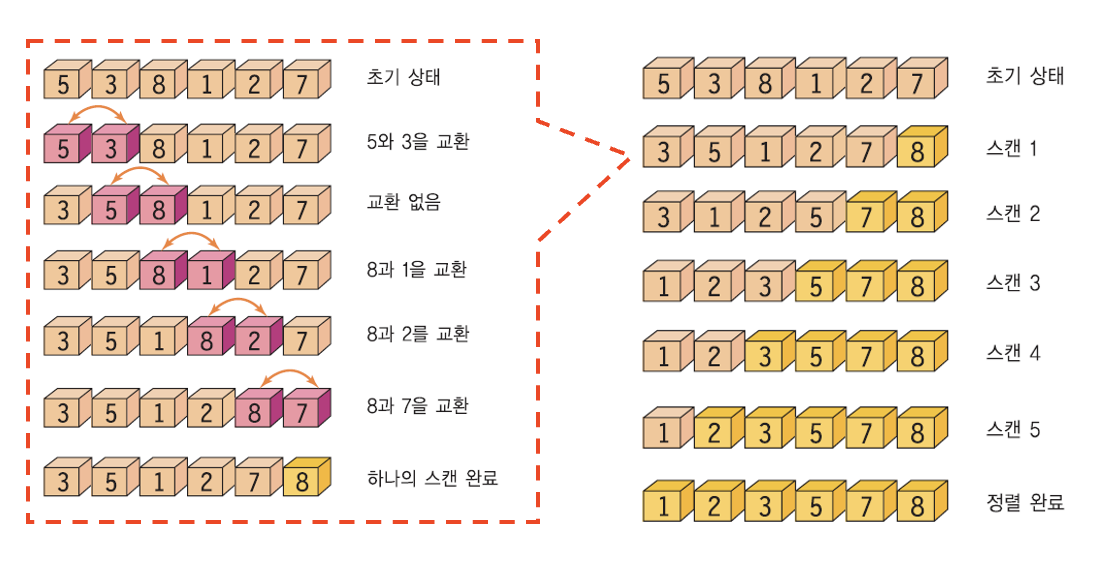
버블 정렬의 과정
- Scan 1: (5, 3)비교 - 5가 더 크므로 교환.
- Scan 1: (5, 8)비교 - 8이 더 크므로 교환x, 다음 레코드 비교
- 위와 같은 과정의 반복 결과로 Scan 1이 종료하게 되면 8이 리스트의 가장 오른쪽에 위치.
- Scan 2: 이전 Scan에서 위치가 결정된 레코드(8)를 제외한 나머지 레코드들을 대상으로 과정 반복.
버블 정렬의 알고리즘 및 구현
// 버블 정렬의 알고리즘 - pseudo code
BubbleSort(A, n)
for i ← n-1 to 1 do // 리스트의 길이만큼 반복
// 0부터 i-1 까지 실행 (각 스캔의 종료후 가장 오른쪽 정렬된 요소는 제외하고 나머지 요소 정렬)
for j ← 0 to i-1 do
j와 j+1번째의 요소가 크기순이 아니면 교환
j++;
i--;
- 가장 바깥쪽의 루프는 리스트의 길이만큼 실행. (scan의 횟수)
또한 index가 내림차순으로 진행되며 내부 for문의 j의 인덱싱에 영향.
j가 i보다 1작은 위치까지만 비교 및 교환을 실행하게 됨.
-> 한번의 스캔 후 가장 오른쪽의 정렬된 요소는 배제- 내부 루프는 각 스캔마다 반복 횟수가 1씩 줄어들며 비교 및 교환 실행.
- 위의 스캔 과정이 n-1번 반복되면 정렬이 끝나게 됨.
// 버블 정렬
#define SWAP(x, y, t) ((t) = (x), (x) = (y), (y) = (t))
void bubble_sort(int list[], int n){
int i, j, temp;
printf("Bubble Sort:\n");
for(i = n - 1; i > 0; i--){
for(j = 0; j < i; j++){
if(list[j] > list[j+1]){
SWAP(list[j], list[j+1], temp);
}
}
}
}
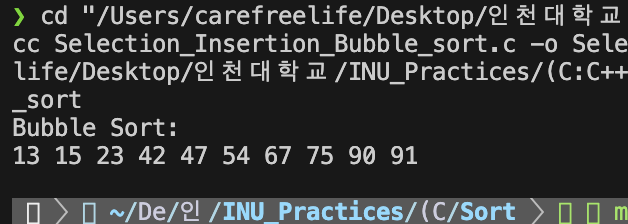
버블 정렬 알고리즘 - 실행 결과버블 정렬의 복잡도 분석
- 비교 횟수 : O(n^2) - 어떠한 경우(최선, 평균, 최악)에도 항상 일정하다.
버블 정렬 알고리즘 - 복잡도 분석- 이동 횟수 :
- 최악 : 대상 자료가 역순으로 정렬되어 있는 경우 - (비교 연산의 횟수 X 3)
- SWAP() 함수가 3번의 이동을 하기 때문.
- 최선 : 대상 자료가 이미 정렬이 되어 있는 경우 - 자료 이동이 발생하지 않는다.
- 버블 정렬의 문제점 :
- SCAN 과정 중 순서에 맞지 않는 요소이더라도 교환하게 된다.
- 일반적으로 레코드의 교환(SWAP)작업이 이동(MOVE)작업보다 더 복잡.
최대한의 설명을 코드 블럭 내의 주석으로 달아 놓았습니다.
혹시 이해가 안가거나 추가적인 설명이 필요한 부분, 오류 등의 피드백은 언제든지 환영합니다!
긴 글 읽어주셔서 감사합니다. 포스팅을 마칩니다.
참고: C언어로 쉽게 풀어쓴 자료구조 <개정 3판> 천인국, 공용해, 하상국 지음
Task Lists
- 정렬(Sorting) 이란?
- 선택 정렬 (Selection Sort) 의 원리
- 선택 정렬의 알고리즘 및 구현
- 삽입 정렬(Insertion Sort) 의 원리
- 삽입 정렬의 알고리즘 및 구현
- 버블 정렬(Bubble Sort) 의 원리
- 버블 정렬의 알고리즘 및 구현




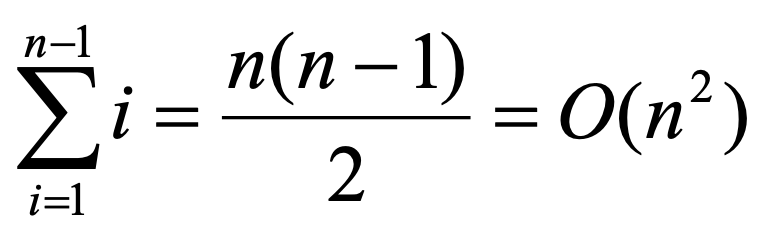



Comments