기수 정렬(Radix Sort)

13 minute read

쉘 정렬(Shell Sort)의 원리

쉘 정렬은 삽입 정렬이 어느 정도 정렬된 배열에 대해서는 대단히 빠른 것에 착안한 방법.
쉘 정렬은 삽입 정렬의 O(n^2) 보다 빠르다.

삽입 정렬은 요소들이 이웃한 위치로만 이동 - 이동 횟수가 많음

쉘 정렬 - 리스트를 일정 간격의 부분리스트로 분류 후 삽입 정렬을 이용하여 정렬.

요소들이 멀리 떨어진 위치로 이동할 수 있음. 1. 전체 리스트를 일정 간격(gap)의 부분 리스트로 나눈다.
2. 나뉘어진 각각의 부분 리스트를 삽입정렬.
3. 모든 부분 리스트가 정렬된 후 전체 리스트를 더 작은 gap을 가진 부분 리스트로 나눠 삽입정렬.
4. 위 과정을 부분 리스트의 개수가 1이 될 때까지 반복.

부분 리스트는 주어진 리스트의 각 k번째 요소를 추출하여 생성. k = 간격(gap)

각 단계마다 k가 작아짐, 각 단계마다 부분리스트에 속하는 레코드들의 개수는 그에 상응하여 증가.

마지막 단계에서는 간격 k의 값이 1이 된다.

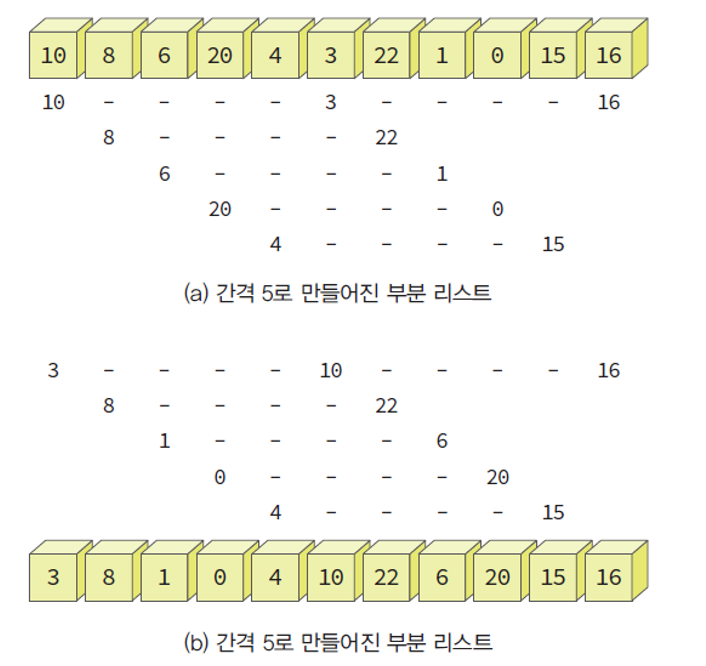
쉘 정렬의 모습

k(gap) = 5

첫번째 부분 리스트 : {10, 3, 16}

두번째 부분 리스트 : {8, 22}

세번째 부분 리스트 : {6, 1}

네번째 부분 리스트 : {20, 0}

다섯번째 부분 리스트 : {4, 15}

각각의 부분 리스트에 대하여 삽입 정렬.

각각의 부분 리스트들이 정렬되면 전체 리스트도 약간씩 정렬됨.

부분 리스트 들은 실제로 생성되는 것이 아니고 일정한 간격으로 삽입 정렬을 수행하는 것 뿐.

추가적인 공간의 생성 X

한번의 단계가 끝나면 k(gap)의 크기를 1/2 줄여 반복.

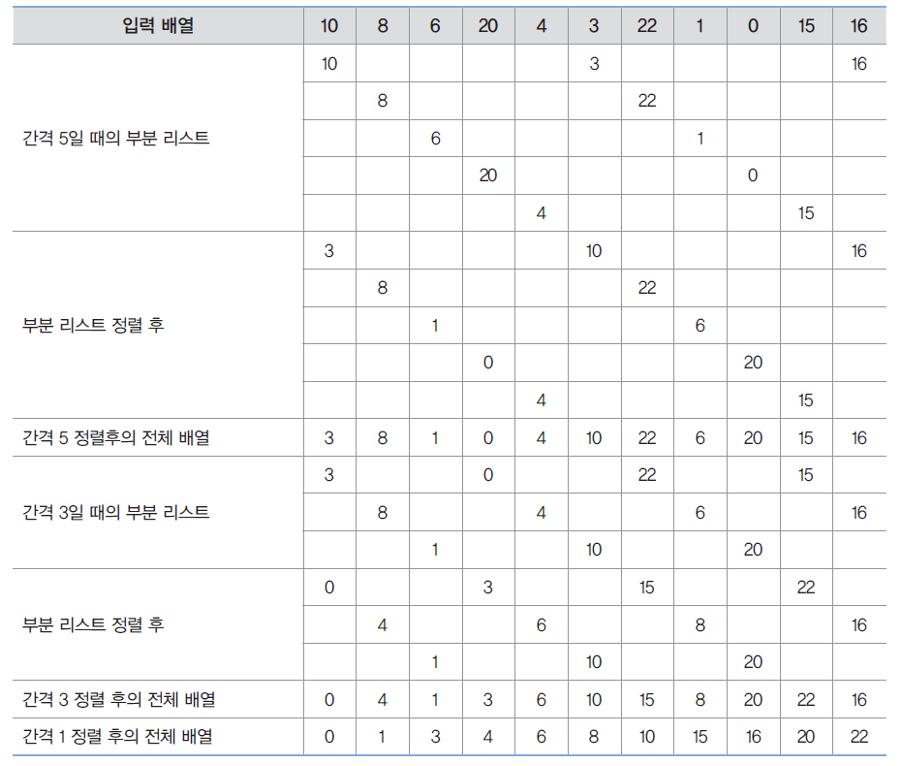
쉘 정렬의 과정

부분 리스트의 개수는 k(gap)이 된다.

간격 k는 홀수인 것이 좋기 때문에 짝수이면 +1을 해준다.

쉘 정렬의 구현

// 쉘 정렬
// gap 만큼 떨어진 요소들을 삽입 정렬
// 정렬의 범위는 first에서 last

void inc_insertion_sort(int list[], int first, int last, int gap){
    int i, j, key;
    // i : 각 부분리스트 요소의 index
    // 시작점 first 에서 gap만큼 떨어진 위치부터 gap 간격마다의 요소를 부분리스트로 설정
    for(i = first + gap; i <= last; i = i + gap){
        key = list[i];
        for(j = i - gap; j >= first && key < list[j]; j = j - gap){
            list[j + gap] = list[j];
        }
        list[j + gap] = key;
    }
}

void shell_sort(int list[], int n){ // n = size
    int i, gap;
    printf("Shell Sort:\n");
    // gap이 1이 될 때까지 gap / 2해가며 진행
    for (gap = n / 2; gap > 0; gap = gap / 2){
        if(gap % 2 == 0)  // gap은 홀수인것이 좋으므로 짝수이면 + 1
            gap++;
        for (i = 0; i < gap; i++){  // 부분 리스트의 개수는 gap과 같음.
            inc_insertion_sort(list, i, n - 1, gap);
        }

    }
}

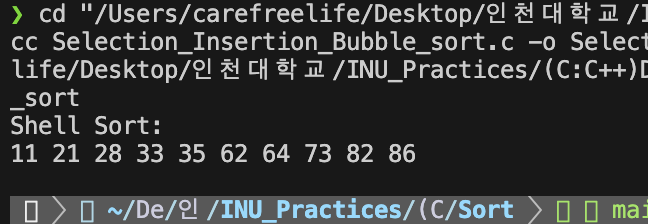
쉘 정렬 알고리즘 - 실행 결과

쉘 정렬의 분석

연속적이지 않은 부분 리스트에서 자료의 교환이 일어나면 한번에 더 큰 거리를 이동한다.

부분 리스트의 개수가 1개가 될 때까지 반복한 결과는 대부분의 정렬이 끝난 상태가 된다.

쉘 정렬은 기본적으로 삽입 정렬을 하며 이때 더욱 빠르게 수행 할 수 있다.

삽입 정렬은 어느정도 정렬이 된 리스트에 대해 빠르게 정렬할 수 있기 때문이다.

쉘 정렬의 시간 복잡도:

최악: O(n^2)

평균: O(n^1.5)

합병 정렬(Merge Sort)의 개념

합병 정렬(Merge Sort) :

1. 하나의 리스트를 두 개의 균등한 크기로 분할 후 분할된 부분 리스트를 정렬
2. 정렬된 두 개의 부분리스트를 합병하여 전체 리스트를 정렬

합병 정렬은 Divide and Conquer(분할 정복) 개념에 바탕을 두고 있다.

Divide and Conquer(분할 정복) :

문제를 더 작게 분할해 해결 후 합하여 기존 문제를 해결하는 방식.
1. 분할(Divide) : 입력 배열을 같은 크기의 2개 배열로 분할.
2. 정복(Conquer) : 부분 배열을 정렬.

만약 부분 배열의 크기가 충분히 작지 않다면 순환 호출을 이용하여 다시 분할.

결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 통합.

합병 정렬 알고리즘의 모습

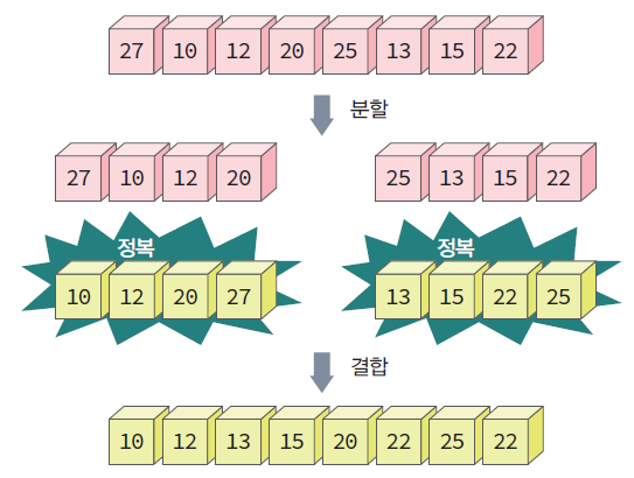
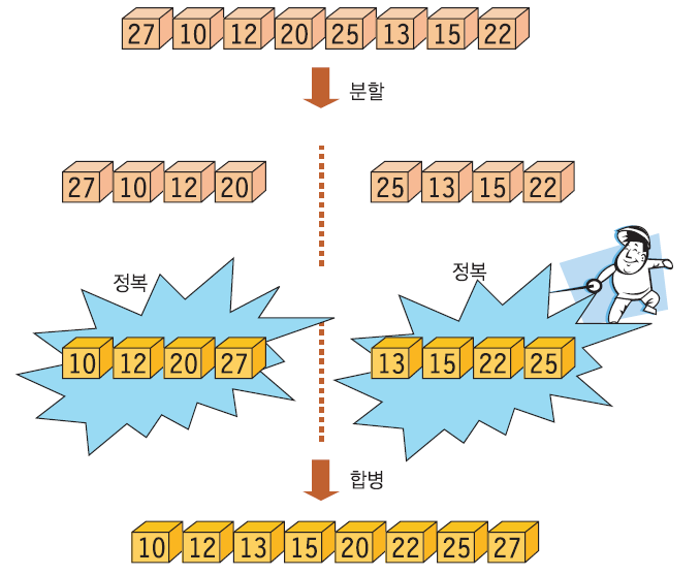
합병 정렬 예시

입력 파일: (27 10 12 20 25 13 15 22)

분할(Divide) : 전체 배열을 (27 10 12 20) 과 (25 13 15 22) 의 2개 부분 배열로 분할
정복(Conquer) : 각 부분 배열 정렬 (10 12 20 27) (13 15 22 25)
결합(Combine) : 2개의 정렬된 부분 배열 통합 (10 12 13 15 20 22 25 27)

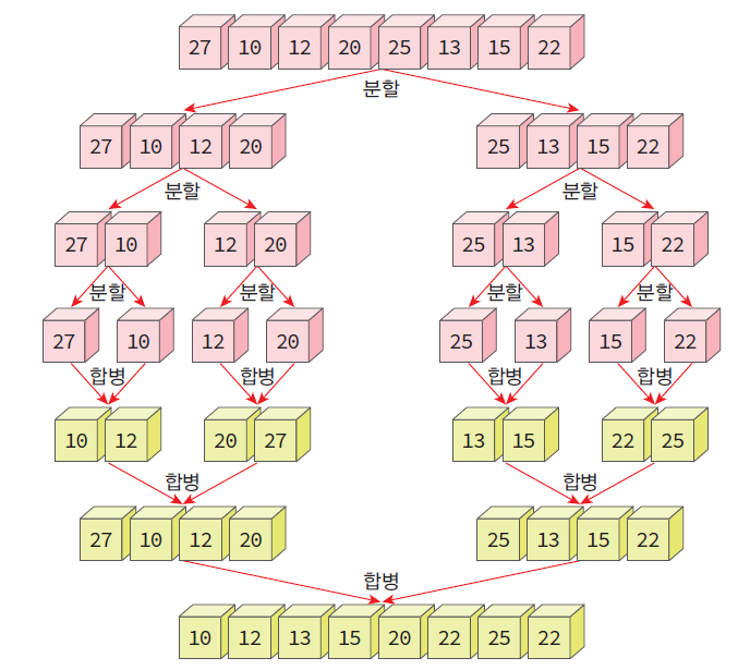
합병 정렬 예시

합병 정렬의 전체 과정

합병 정렬(Merge Sort) 알고리즘

// 합병 정렬 알고리즘 - pseudo code

merge_sort(list, left, right)
    // 만약 나누어진 구간의 크기가 1 이상이면
    if left < right 
        mid = (left + right) / 2;         // 중간 위치를 계산한다.
        merge_sort(list, left, mid);      // 앞 부분(left ~ mid) 배열을 정렬
        merge_sort(list, mid + 1, right); // 뒷 부분(mid+1 ~ right) 배열을 정렬 
        // 정렬된 앞, 뒤 부분 배열을 통합하여 하나의 정렬된 배열 생성
        merge(list, left, mid, right);    

합병 정렬 알고리즘에서 실질적인 정렬이 이루어지는 부분은 합병(merge) 단계이다.

합병(merge) 알고리즘은 합병 결과를 저장할 추가적인 리스트 하나를 필요로 한다.

분할된 리스트의 요소중 더 작은 요소를 새로 생성한 리스트에 추가해 나간다. (비교)

두 리스트 중 하나가 끝날 때까지 반복.

한 리스트의 요소가 전부 새로운 리스트에 추가되면 남아있는 리스트의 요소들을 그대로 새 리스트에 복사

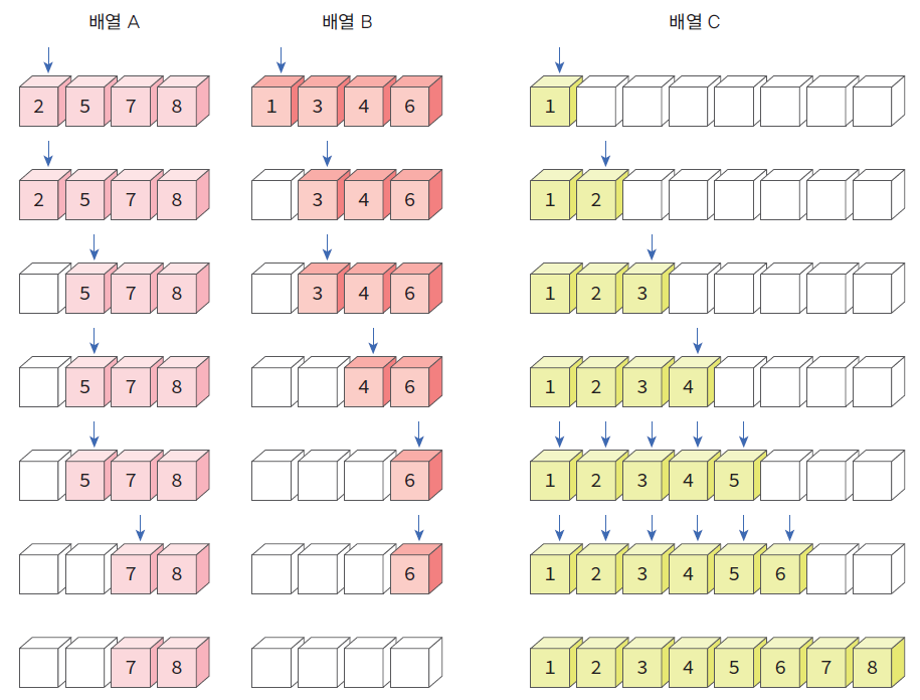
합병 정렬 알고리즘 - 과정

합병 (merge) 알고리즘

// 합병 알고리즘 (merge) - pseudo code

// 두 개의 인접한 배열 list[left ~ mid] 와 list[mid+1 ~ right]을 합병
merge(list, left, mid, right)
    i ← left;
    j ← mid + 1;
    k ← left;
    sorted[] 배열 생성;
    while i <= mid and j <= right do
        if(list[i] < list[j]
            then
                sorted[k] ← list[i];
                k++;
                i++;
            else
                sorted[k] ← list[j];
                k++;
                j++;
    요소가 남아있는 부분 배열을 sorted로 복사;
    sorted를 list로 복사;

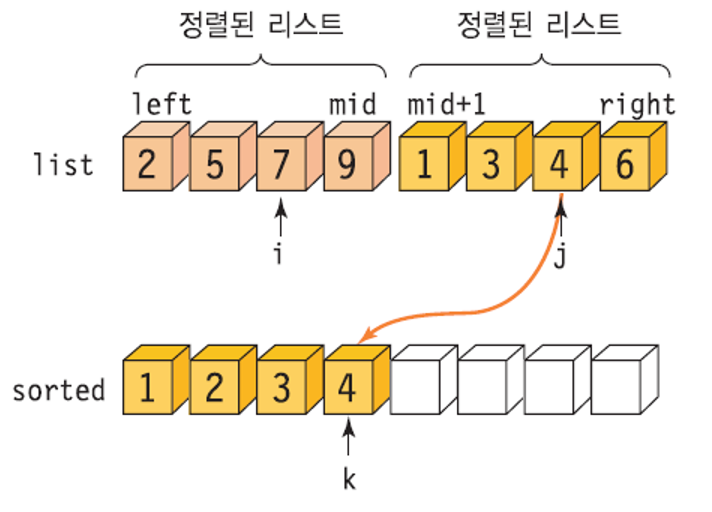
위의 합병 알고리즘에서 하나의 배열 안에 두 개의 부분 리스트가 있다 가정

왼쪽 부분 리스트의 범위: left ~ mid

오른쪽 부분 리스트의 범위: mid+1 ~ right

합병된 부분 리스트를 임시 저장하기 위해 추가적인 배열 sorted[] 사용

합병 정렬 알고리즘 - merge()

합병 정렬의 구현

merge_sort() 함수에서 주어진 list 배열을 2등분 하여 각각의 부분 배열에 대해 재귀 호출.

부분 배열에 요소가 하나 남을 때까지 재귀 호출.

분할 과정이 끝나면 merge() 함수에서 비교 및 합병 과정을 실행. (실제 정렬이 실행되는 함수)

비교 및 합병 후 정렬된 복사본 리스트를 기존 리스트에 복사.

// 합병 정렬
int sorted[MAX_SIZE]; // 정렬 및 합병되어질 공간 생성

/* 
i 는 정렬된 왼쪽 리스트에 대한 인덱스
j 는 정렬된 오른쪽 리스트에 대한 인덱스
k 는 정렬될 리스트에 대한 인덱스
*/
void merge(int list[], int left, int mid, int right){
    int i, j, k, l;
    i = left; j = mid + 1; k = left;

    // 각 부분 리스트에 대하여 sorted 배열에 정렬
    // 두 부분 리스트 중 하나의 요소가 전부 사용될 때까지.
    while (i <= mid && j <= right){
        if(list[i] <= list[j])
            sorted[k++] = list[i++];
        else
            sorted[k++] = list[j++];
    }
    // 남아 있는 요소의 일괄 복사 to sorted[]
    if(i > mid) // 오른쪽 리스트가 남아있을 시
        for(l = j; l <= right; l++)
            sorted[k++] = list[l];
    else    // 왼쪽 리스트가 남아있을 시
        for(l = i; l <= mid; l++)
            sorted[k++] = list[l];
    // 배열 sorted[] 의 요소를 배열 list[] 로 재 복사.
    for(l = left; l <= right; l++){
        list[l] = sorted[l];
    }
}

void merge_sort(int list[], int left, int right){
    int mid;
    if(left < right){
        mid = (left + right) / 2;   // 리스트의 중간 인덱스 찾기

        // 왼 부분 리스트 생성 가장 왼쪽 인덱스(0) ~ 중간 인덱스(mid) 
        merge_sort(list, left, mid);

        // 오른 부분 리스트 생성 중간 바로 다음 인덱스 (mid+1) ~ 가장 오른쪽 인덱스(right)
        merge_sort(list, mid + 1, right);

        // 부분 리스트의 정렬 및 합병
        merge(list, left, mid, right);
    }
}

합병 정렬 알고리즘 - 실행 결과

합병 정렬의 복잡도 분석

합병 정렬은 순환 호출로 구성된다.

비교 횟수: O(n) X h(트리의 높이 == 순환 호출의 깊이)

완전 이진 트리의 leaf 노드 개수 세는 것과 비슷하다.

n : leaf 노드의 개수.

h : log_2 n == 합병의 횟수(순환 호출의 깊이)

배열이 부분 배열로 나누어지는 단계에서는 비교 / 이동 연산이 수행되지 않는다.

부분 배열이 합쳐지는 merge() 함수에서 비교 및 이동 연산이 실행됨.

순환 호출의 깊이 만큼의 합병 단계가 필요하다.

따라서, 순환 호출의 깊이(h = log_2 n) X 비교 연산(n) == O(n * log_2 n)

이동 횟수:

총 부분 배열에 들어있는 요소가 n개 라고 한다면, 레코드의 이동이 2n 번 발생.

비교와 마찬가지로 합병 단계 만큼의 이동이 필요하므로 O(2n * log_2 n)

결국 합병 정렬의 시간복잡도는 O(n * log_2 n)으로 나타낼 수 있다.

합병 정렬의 장점 :

합병 정렬은 정렬간에 같은 값은 기존 위치를 유지하는 안정적인 알고리즘 이다.

입력되는 데이터의 성질에 상관없이 최악, 평균, 최선 모두 O(n * log_2 n)의 시간 복잡도를 가진다.

합병 정렬의 단점:

추가적인 임시 배열의 공간을 필요로 함.

레코드의 크기가 큰 경우, 이동 횟수가 많으므로 큰 시간적 낭비.

레코드를 연결 리스트로 구성한다면, 데이터의 이동은 무시할 수 있을 정도로 작아짐.

이 경우, 합병 정렬은 그 어떤 정렬 알고리즘보다 효율적임.

퀵 정렬의 개념 (Quick Sort)

퀵 정렬(Quick Sort)은 평균적으로 매우 빠른 수행속도를 가짐.
Divide and Conquer(분할 정복)에 근거하는 알고리즘.
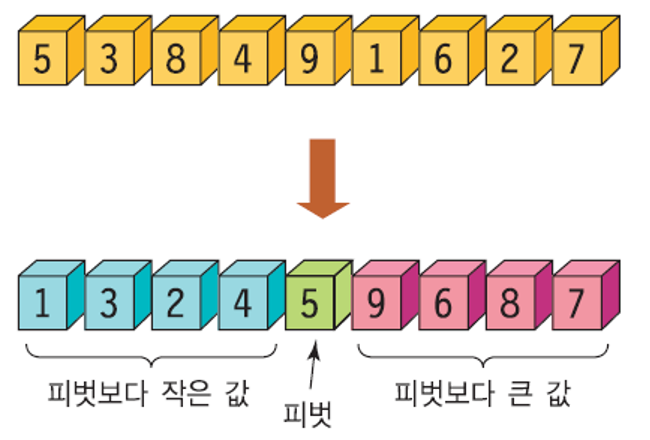
리스트의 한 요소를 피벗(pivot) 으로 선택.
피벗보다 작은 요소들의 부분 리스트, 피벗보다 큰 요소들의 부분 리스트로 분할.
피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 정렬하게 되면 전체 리스트가 정렬됨.

퀵 정렬 알고리즘

퀵 정렬 함수는 부분 리스트에 대하여 순환 호출.

부분 리스트 에서도 다시 피봇을 정하고 피봇을 기준으로 2개의 리스트로 분할하는 과정이 반복.

부분 리스트들이 더 이상 분할 되지 않을 때까지 분할.

퀵 정렬 알고리즘

// 퀵 정렬
void quick_sort(int list[], int left, int right)
    // 정렬할 범위가 2개 이상의 데이터라면
    if(left < right) {
        // partition 함수 호출 (피벗을 기준으로 2개의 리스트로 분할 및 피벗의 위치 반환)
        int q = partition(list, left, right);
        // left(0) ~ 피벗 직전(q-1)까지 순환 호출
        quick_sort(list, left, q-1);
        // 피벗 이후(q+1)부터 끝까지(right) 순환 호출
        quick_sort(list, q+1, right);

퀵 정렬에서 가장 중요한 함수는 partition()

partition()

초기 입력 배열을 pivot을 기준으로 2개의 부분 리스트로 분할.

피벗보다 작은 요소는 왼쪽 부분리스트 / 큰 요소는 오른쪽 부분리스트에 존재

리스트의 첫번째 요소를 pivot으로 설정. (편의를 위해)

pivot 이후의 요소중 첫번째 요소는 low, 마지막 요소는 high로 설정.

low는 1씩 증가시키며 pivot 보다 높은 값을 만나면 해당 위치에서 멈춤.

high는 1씩 감소시키며 pivot 보다 낮은 값을 만나면 해당 위치에서 멈춤.

low와 high가 전부 멈추게 되면 두 요소를 바꿈.

리스트 내에서 점진적으로 low는 증가, high는 감소하므로 두 요소가 엇갈리기 전까지 반복.

low와 high의 인덱스가 엇갈리게 되면 high는 직전의 low가 가리키던 값을 가리키게 되고 low는 직전에 high가 가르키던 값을 가리키게 됨.

따라서 현재 low는 pivot보다 큰 값, high는 pivot보다 작은 값을 가리키고 있음.

이 때 high/low 의 경계선이 pivot을 기준으로 작은 값/큰 값 으로 나뉜 것

pivot과 high의 요소 및 위치를 바꾸어주면 리스트는 pivot을 기준으로 (왼쪽 - 작은값) (오른쪽 - 큰값) 으로 분할됨.

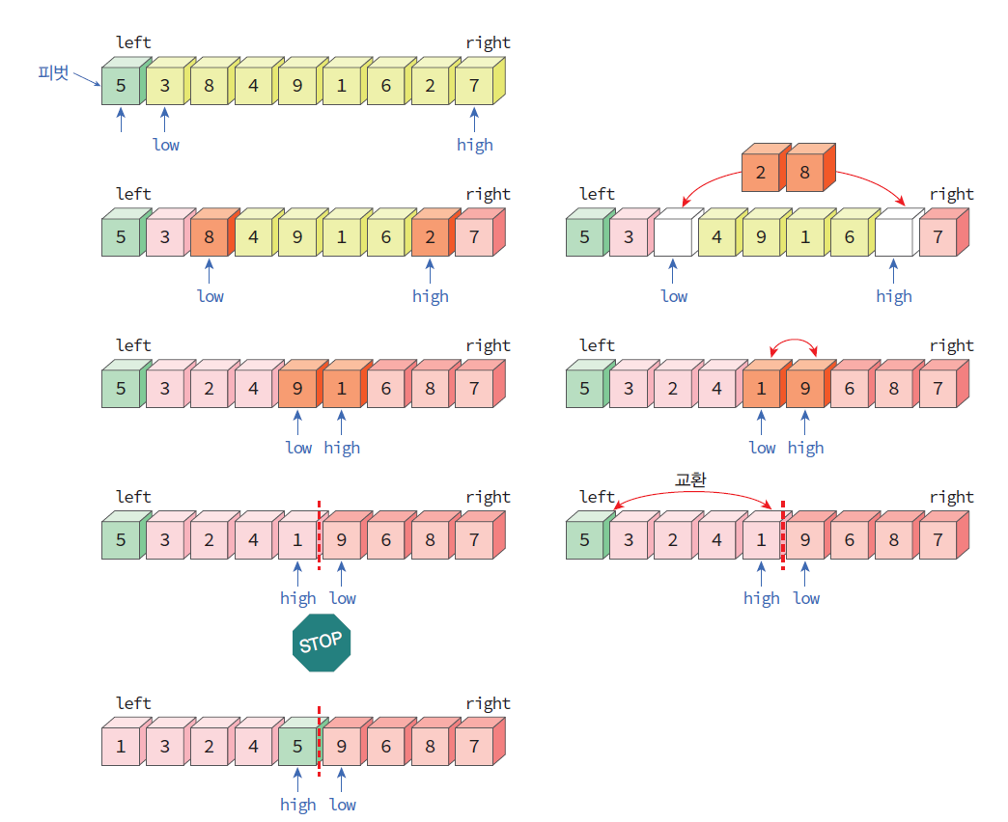
퀵 정렬의 분할 과정 - partition()

‼️정리‼️

low와 high를 양 끝에서 출발.

서로 부적절한 데이터를 만나면 교환.

low와 high의 index가 엇갈린 직후 pivot과 high의 요소 및 위치를 교환.

pivot 기준 좌, 우 리스트가 작은 값, 큰 값으로 분할됨.

partition() 의 구현

// 퀵 정렬
int partition(int list[], int left, int right){
    int pivot, temp;
    int low, high;

    // left는 pivot의 위치이지만 for문 들어가며 +1 증가되어 피봇 다음 index부터 시작하게 된다.
    low = left;
    // high도 마찬가지로 for문 들어가며 -1 감소되어 시작되기 때문에 배열을 넘어서는 인덱스부터 시작.
    high = right + 1;
    // 편의를 위해 피봇을 list의 첫 인덱스로 설정.
    pivot = list[left];

    do {
        // 두 개의 do-while문
        do
            low++;
        while (list[low] < pivot);
        // low가 pivot보다 큰 (low 부분 리스트에 있으면 안되는) 요소에서 멈춤
        
        do
            high--;
        while (list[high] > pivot);
        // high가 pivot보다 작은 (high 부분 리스트에 있으면 안되는) 요소에서 멈춤

        // 위의 do while문에 의해 멈춰 있는 low / high 가 가리키고 있는 요소를 교환.
        // (부적절한 요소가 있는 위치)
        if(low < high) SWAP(list[low], list[high], temp);
    }while (low < high); // low와 high가 교차하면 종료

    // pivot(list[left])과 high의 요소를 바꾸어준다.
    SWAP(list[left], list[high], temp);
    
    return high;    // high가 가리키는 곳으로 이동한 pivot의 인덱스를 반환
}

partition() 함수가 한번 실행되어 pivot을 기준으로 좌우 데이터가 분할되면
왼쪽 부분 리스트는 pivot 보다 작은 요소 / 오른쪽 부분 리스트는 pivot 보다 큰 요소로 분할됨.

따라서 pivot의 위치는 고정된다.
이후 pivot을 제외한 좌 / 우 부분 리스트에 대해서만 퀵 정렬을 실행하면 전체 리스트가 정렬된다.

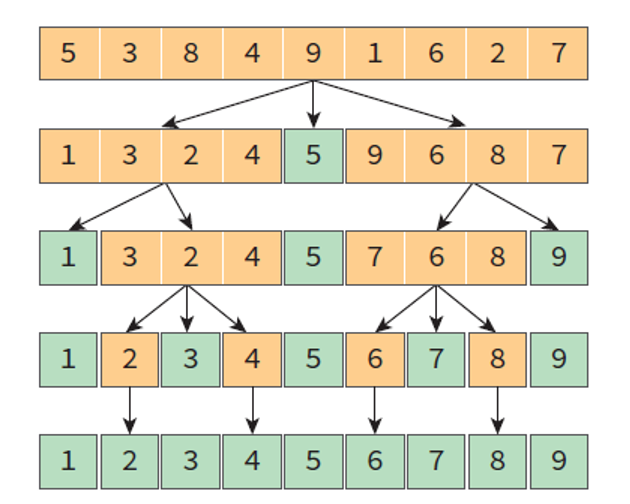
퀵 정렬 알고리즘 - 전체 과정

퀵 정렬 전체 코드

// 퀵 정렬
int partition(int list[], int left, int right){
    int pivot, temp;
    int low, high;

    // left는 pivot의 위치이지만 for문 들어가며 +1 증가되어 피봇 다음 index부터 시작하게 된다.
    low = left;
    // high도 마찬가지로 for문 들어가며 -1 감소되어 시작되기 때문에 배열을 넘어서는 인덱스부터 시작.
    high = right + 1;
    // 편의를 위해 피봇을 list의 첫 인덱스로 설정.
    pivot = list[left];

    do {
        // 두 개의 do-while문
        do
            low++;
        while (list[low] < pivot);
        // low가 pivot보다 큰 (low 부분 리스트에 있으면 안되는) 요소에서 멈춤
        
        do
            high--;
        while (list[high] > pivot);
        // high가 pivot보다 작은 (high 부분 리스트에 있으면 안되는) 요소에서 멈춤

        // 위의 do while문에 의해 멈춰 있는 low / high 가 가리키고 있는 요소를 교환.
        // (부적절한 요소가 있는 위치)
        if(low < high) SWAP(list[low], list[high], temp);
    }while (low < high); // low와 high가 교차하면 종료

    // pivot(list[left])과 high의 요소를 바꾸어준다.
    SWAP(list[left], list[high], temp);
    
    return high;    // high가 가리키는 곳으로 이동한 pivot의 인덱스를 반환
}

void quick_sort(int list[], int left, int right){
    if(left < right){
        // partition() 함수의 결과로 pivot 생성 후 리스트 분할.
        int pivot = partition(list, left, right);
        // left ~ pivot 전 요소까지 퀵 정렬
        quick_sort(list, left, pivot - 1);
        // pivot 이후 요소부터 right(끝)까지 퀵 정렬.
        quick_sort(list, pivot + 1, right);
    }
}

퀵 정렬 알고리즘 - 실행 결과

퀵 정렬의 복잡도 분석

이진 트리의 높이가 낮을 때 교환 수가 최소.

균등한 리스트(완전 이진트리) 인 경우 최선의 시간복잡도 도출가능.

O(n * log_2 n)

경사 이진 트리인경우 최악의 시간복잡도 도출.

O(n^2) pivot이 초기 입력리스트의 중간 값에 가까울수록 퀵 정렬의 효율성 증대.

random sampling :

랜덤으로 몇가지 요소를 꺼내 그 평균과 비슷한 값을 pivot으로 지정.

기수 정렬(Radix Sort)

대부분의 정렬 알고리즘은 모두 레코드들을 비교함으로써 정렬을 수행.
기수 정렬(Radix Sort)는 레코드를 비교하지 않고 정렬을 수행 할 수 있다.
- 비교에 의한 정렬 알고리즘의 하한(최선)인 O(n * log_2 n) 보다 좋을 수 있다.
- 기수 정렬은 O(dn)의 시간 복잡도를 가진다. (대부분 d < 10)

기수(Radix) : 숫자의 자리수.

42 : (10의 자리수 4, 1의 자리수 2) 4, 2는 기수이다.

기수 정렬 == 다단계 정렬 : 단계의 수는 데이터의 자리수와 일치.

십진수는 0~9 까지 10개의 값을 가진다.

10개의 버킷을 만들어 입력 데이터를 각 자리수의 값에 상응하는 상자에 넣는다.

첫 상자부터 담겨있는 데이터를 순차적으로 읽어 데이터를 정렬.

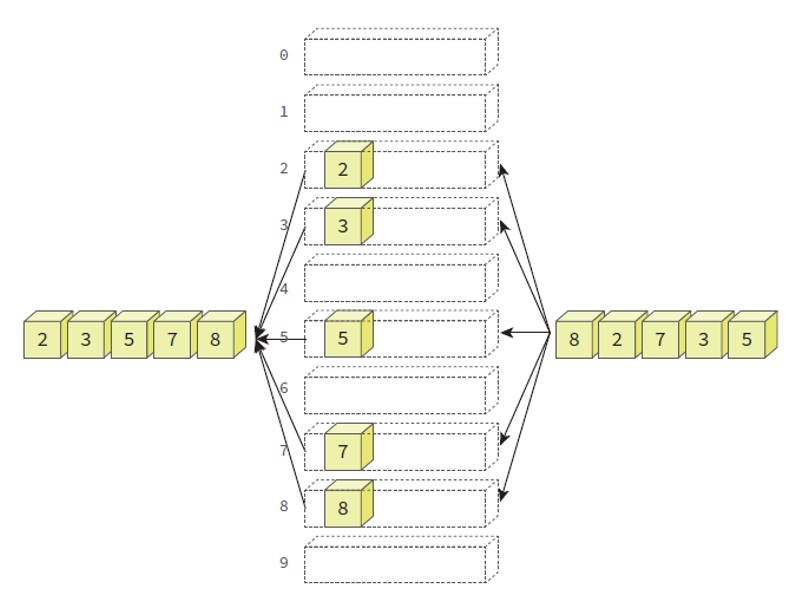
한 자리수 기수 정렬의 모습

비교 연산을 사용하지 않으며, 단순히 각 자리수의 값에 맞춰 상자에 넣고 빼는 동작의 되풀이.

2개 이상의 자리수로 이루어진 수도 정렬이 가능하다.

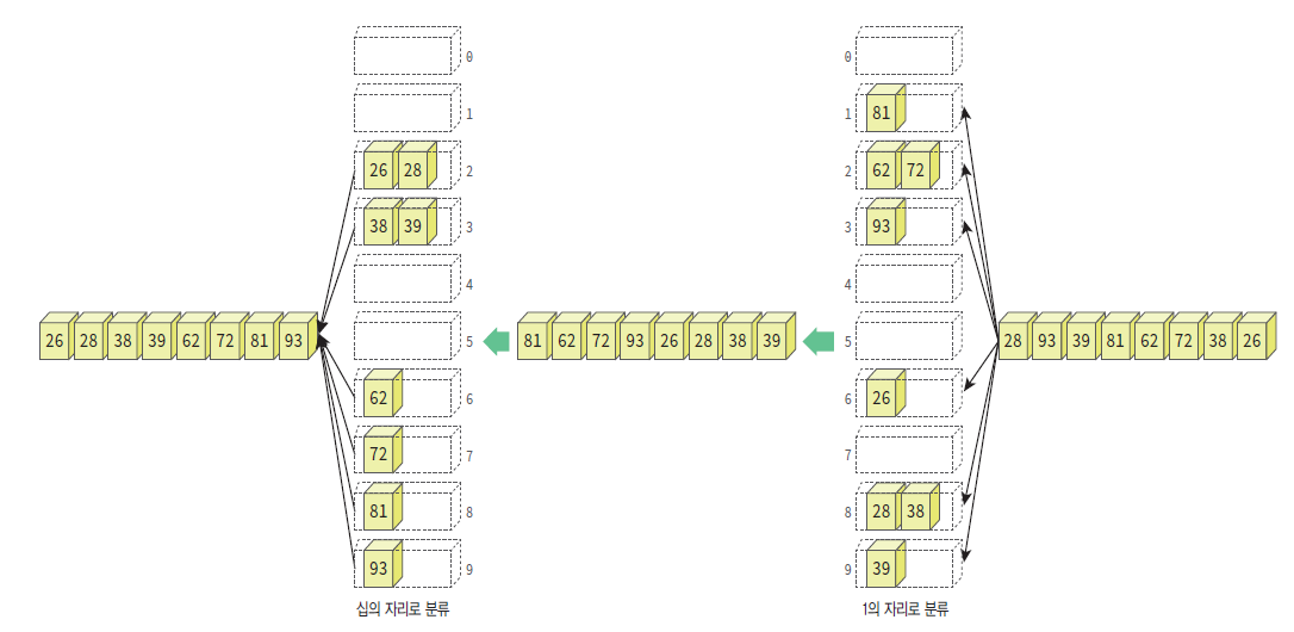
각 자리수마다 버킷을 따로 사용하여 자리수 별로 정렬.

낮은 자리수부터 버킷에 삽입하여 정렬 후 높은 자리수를 정렬해나간다.

예) 1의 자리수를 기준으로 버킷 0~9 에 삽입하여 정렬.

10의 자리수를 기준으로 버킷 0~9에 삽입하여 정렬.

두 자리수 기수 정렬의 모습

기수 정렬의 알고리즘

LSD(Least Significant Digit) : 가장 낮은 자리수.
MSD(Most Significant Digit) : 가장 높은 자리수.

// 기수 정렬 알고리즘 - pseudo code

RadixSort(list, n):

for d ← LSD의 위치 to MSD의 위치 do {
    d번째 자리수에 따라 0번부터 9번 버킷에 삽입.
    버킷에서 숫자들을 순차적으로 읽어 하나의 리스트로 합친다.
    d++;
}

버킷은 큐로 구현 : 가장 먼저 들어간 숫자가 먼저 나와야 함.

버킷의 개수는 key의 표현 방법과 밀접한 관계를 가진다.

이진법을 사용한다면 두개의 버킷만 있으면 데이터의 구분이 가능. (0,1)

알파벳을 사용한다면 26개의 버킷이 있어야 모든 데이터의 구분이 가능. (A~Z)

십진법을 사용한다면 10개의 버킷이 있어야 모든 데이터의 구분이 가능. (0~9)

예) 32비트의 정수인 경우, 8비트씩 나누면 버킷은 256개로 늘어나지만 필요한 패스의 수가 4개로 줄어든다.

기수 정렬의 구현

// 6장의 큐 소스를 여기에...
#define BUCKETS 10
#define DIGITS 4
void radix_sort(int list[], int n)
{
    int i, b, d, factor=1;
    QueueType queues[BUCKETS];
    
    for(b=0;b<BUCKETS;b++) 
        init(&queues[b]); // 큐들의 초기화
    
    for(d=0; d<DIGITS; d++){
        for(i=0;i<n;i++) // 데이터들을 자리수에 따라 큐에 입력
            enqueue( &queues[(list[i]/factor)%10], list[i]);

        for(b=i=0;b<BUCKETS;b++) // 버켓에서 꺼내어 list로 합친다.
            while( !is_empty(&queues[b]) )
                list[i++] = dequeue(&queues[b]);
        factor *= 10; // 그 다음 자리수로 간다.
    }
}

기수 정렬의 복잡도 분석

n개의 레코드, d개의 자릿수로 이루어진 키를 기수 정렬할 경우

메인 루프는 자리수 d번 반복.

큐에 n개 레코드 입력 수행.

O(dn)의 시간 복잡도 (사실상 O(n))

키의 자리수 d는 10 이하의 작은 수 이므로 빠른 정렬이라고 할 수 있다.

실수, 한글, 한자로 이루어진 키는 경우의 수가 매우 많아 정렬하지 못한다.

ex) 궭, 꿿, 갉 (…)

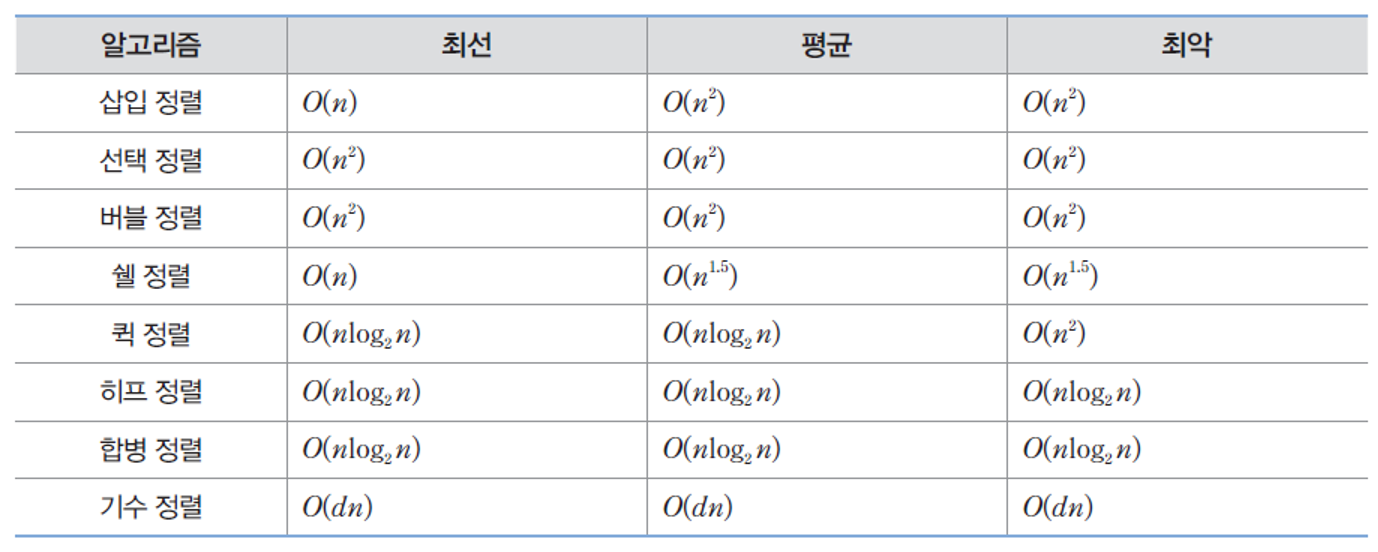
정렬 알고리즘의 비교

정렬 알고리즘의 비교

최대한의 설명을 코드 블럭 내의 주석으로 달아 놓았습니다.

혹시 이해가 안가거나 추가적인 설명이 필요한 부분, 오류 등의 피드백은 언제든지 환영합니다!

긴 글 읽어주셔서 감사합니다. 포스팅을 마칩니다.

처음으로~

참고: C언어로 쉽게 풀어쓴 자료구조 <개정 3판> 천인국, 공용해, 하상국 지음

Task Lists

Twitter Facebook LinkedIn

Chae Seungmin

[Data Structure]
정렬(Sort)(2) - 쉘 정렬(Shell Sort) / 합병 정렬(Merge Sort) / 퀵 정렬(Quick Sort) / 기수 정렬(Radix Sort)

쉘 정렬(Shell Sort)의 원리

쉘 정렬의 구현

합병 정렬(Merge Sort)의 개념

합병 정렬 예시

합병 정렬(Merge Sort) 알고리즘

합병 (merge) 알고리즘

합병 정렬의 구현

합병 정렬의 복잡도 분석

퀵 정렬의 개념 (Quick Sort)

퀵 정렬 알고리즘

‼️정리‼️

partition() 의 구현

퀵 정렬 전체 코드

기수 정렬(Radix Sort)

기수 정렬의 알고리즘

기수 정렬의 구현

기수 정렬의 복잡도 분석

정렬 알고리즘의 비교

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)

※블로그 이전 안내※

Chae Seungmin

쉘 정렬(Shell Sort)의 원리

쉘 정렬의 구현

합병 정렬(Merge Sort)의 개념

합병 정렬 예시

합병 정렬(Merge Sort) 알고리즘

합병 (merge) 알고리즘

합병 정렬의 구현

합병 정렬의 복잡도 분석

퀵 정렬의 개념 (Quick Sort)

퀵 정렬 알고리즘

‼️정리‼️

partition() 의 구현

퀵 정렬 전체 코드

기수 정렬(Radix Sort)

기수 정렬의 알고리즘

기수 정렬의 구현

기수 정렬의 복잡도 분석

정렬 알고리즘의 비교

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)