Data Structure : (5) 스택(Stack)

16 minute read

Data Structure :: 스택 (Stack)

스택 (Stack) 이란?

사진출처:[우리집]

"스택이란, 쌓여있는 객체이다."

일상 생활에서 스택은 우리 주변에 항상 존재한다. 심지어 이삿짐 위에 버티고 앉아있는 우리 단비까지도 스택이라고 할 수 있다.

층층이 쌓여진 아파트, 헬스장에 쌓여있는 원판, 카페에 쌓여있는 일회용 용기까지 모두 스택이라고 할 수 있다.

이처럼 스택이란 어떠한 객체들이 쌓여있는 형태를 말한다.

스택의 특징

후입선출(LIFO: Last-In First-Out)

위 사진처럼 스택에서의 입출력은 가장 윗단에서만 일어나고
그 외의 위치에서는 데이터의 삭제가 이루어지지 못한다.

후입선출

자료구조에서의 스택은 자료의 출력 순서가 입력 순서의 역순으로 이루어져야 할 경우에 매우 요긴하게 사용된다.

ex. (a, b, c, d, e) 형태의 데이터를 (e, d, c, b, a) 와 같은 역순으로 정렬하고 싶을때 스택에 데이터를 전부 입력 후 출력을 하게되면 후입선출: LIFO (가장 늦게 입력된 데이터가 가장 먼저 출력된다.) 원리에 따라 데이터가 역순으로 정렬된다.

스택의 구조

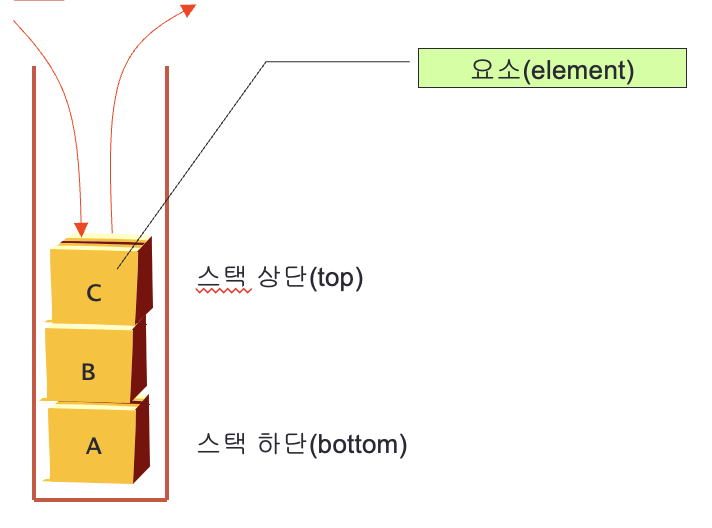
스택의 구조

스택 상단(stack top): 스택에서 입출력이 이루어지는 부분

스택 하단(stack bottom): 스택의 바닥부분. 가장 먼저 입력된 요소가 있다.

요소(element): 스택에 저장되는 것

공백 스택(empty stack): 스택에 요소가 하나도 없는 비어있는 스택.

시스템 스택을 이용한 함수 호출

프로그래밍을 할 때 수많은 함수들이 호출되어 실행되는 것을 볼 수 있다.

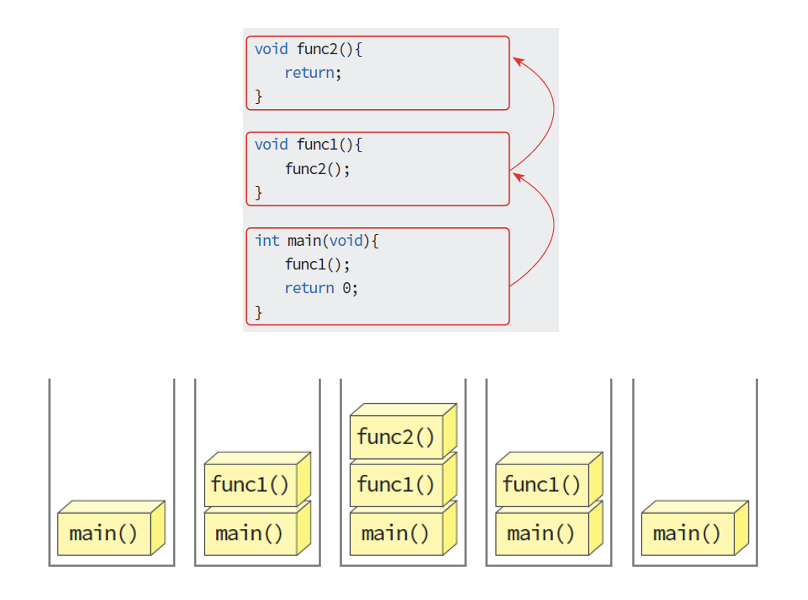
함수는 호출이 되어 실행이 된 후 자신을 호출한 함수로 돌아가야 하는데 이때 스택이 사용된다.

함수는 들어온 길을 되돌아가야 하기 때문이다.
즉, 호출된 순서의 역순으로 빠져나가야 한다.

이처럼 스택은 함수가 복귀할 주소를 저장하는 데에 사용된다.

시스템 스택

함수 호출 과정에서의 스택 응용(시스템 스택)

시스템 스택에는 함수가 호출될 때마다 활성 레코드(activation record)가 만들어지고, 이곳에 복귀 주소가 저장된다.

활성 레코드에는 프로그램 카운터 뿐만 아니라 함수 호출시의 매개변수와 함수 내부에서 선언된 지역변수들이 같이 생성된다.

자기 자신을 호출하는 재귀 함수 (recursion) 도 동일한 방법으로 활성 레코드가 생성된 후 사라진다.
순환(recursion)에 대해 더 궁금하다면? ➡️ 순환 - Recursion

스택의 추상 데이터 타입(ADT)

∙객체: 0개 이상의 원소를 가지는 유한 선형 리스트

∙연산:  
  ▪ create(size) ::= 최대 크기가 size인 공백 스택을 생성한다.

    // 스택이 포화 상태인지 검사
  ▪ is_full(s) ::=
  	  if(스택의 원소수 == size) return TRUE;
  	  else return FALSE;

    // 스택이 공백 상태인지 검사
  ▪ is_empty(s) ::= 
  	  if(스택의 원소수 == 0) return TRUE;
  	  else return FALSE;
    
    // 스택의 top에 요소를 추가
  ▪ push(s, item) ::= 
  	  if( is_full(s) ) return ERROR_STACKFULL;
  	  else 스택의 맨 위에 item을 추가한다.
    
    // 스택의 top에 있는 요소를 삭제 후 반환
  ▪ pop(s) ::= 
  	  if( is_empty(s) ) return ERROR_STACKEMPTY;
  	  else 스택의 맨 위의 원소를 제거해서 반환한다. 

    // 스택의 top에 있는 요소를 탐색
  ▪ peek(s) ::= 
  	  if( is_empty(s) ) return ERROR_STACKEMPTY;
  	  else 스택의 맨 위의 원소를 제거하지 않고 반환한다. 

스택의 연산

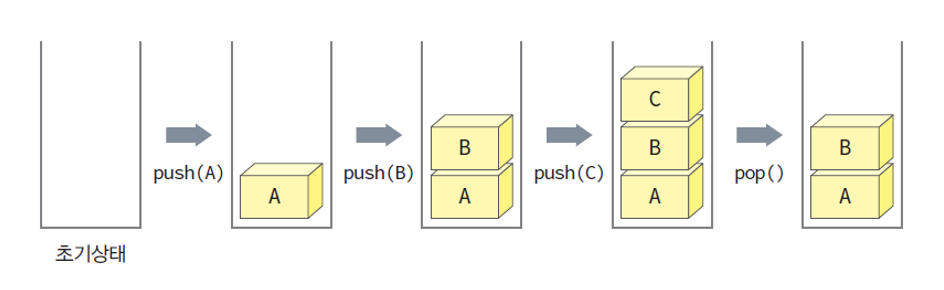
스택의 push() & pop() 연산 과정

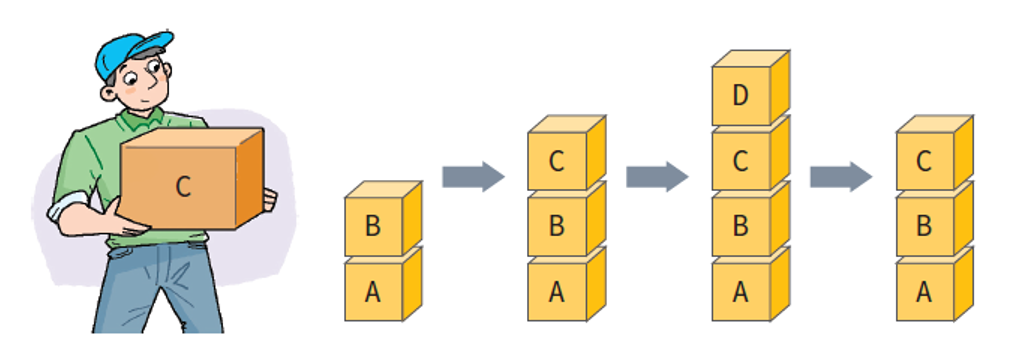
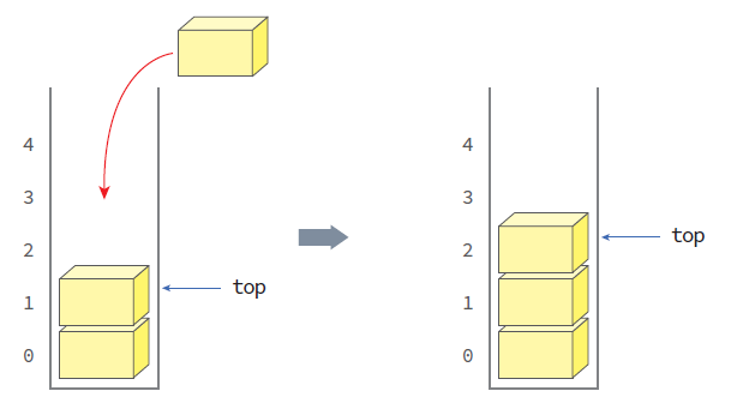
push() : 스택에 데이터(요소)를 추가.

생성된 스택의 가장 밑부분 부터 데이터를 쌓는다.

만약 스택의 상태가 full한 상태에서 push()를 하게 되면 오류가 발생한다.

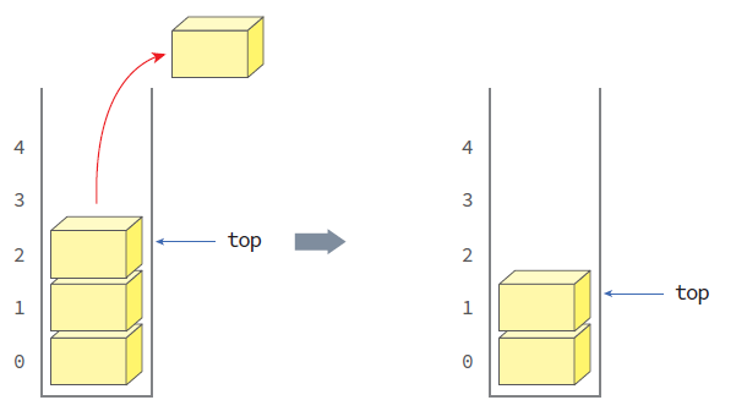
pop() : 스택에서 데이터(요소)를 삭제.

스택의 가장 윗부분(top)의 데이터를 꺼내 삭제한다.

스택에 더 이상 남아있는 데이터가 없는 상태에서 pop()을 한다면 오류가 발생한다.

스택의 구현

스택을 구현하는 방법 두 가지

Array를 이용해 구현

간단하고 성능이 우수하다.

스택의 크기가 고정됨(fixed).

Linked List를 이용해 구현

구현하는 과정이 복잡하다.

스택의 크기를 동적으로 할당 가능.

스택의 구현 : 배열

배열을 이용해 스택을 구현해보자.

배열로 구현한 스택의 구조

배열에는 다양한 type의 요소들을 넣을 수 있다. 예제에서는 int형 정수가 저장되는 것으로 하겠다.

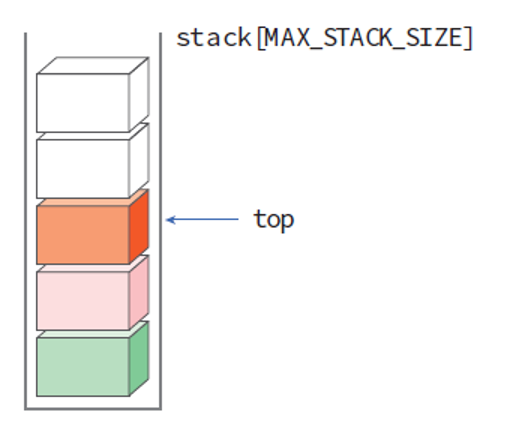
int형 정수를 저장해야 하니 int형의 1차원 배열 stack[MAX_STACK_SIZE]을 생성하도록 하자.

스택에서 가장 최근에 입력된 데이터를 가리키는 변수 top도 생성해주자.

가장 먼저 입력된 순서대로 stack[0] 부터 stack[top] 까지 저장 될 것이다.

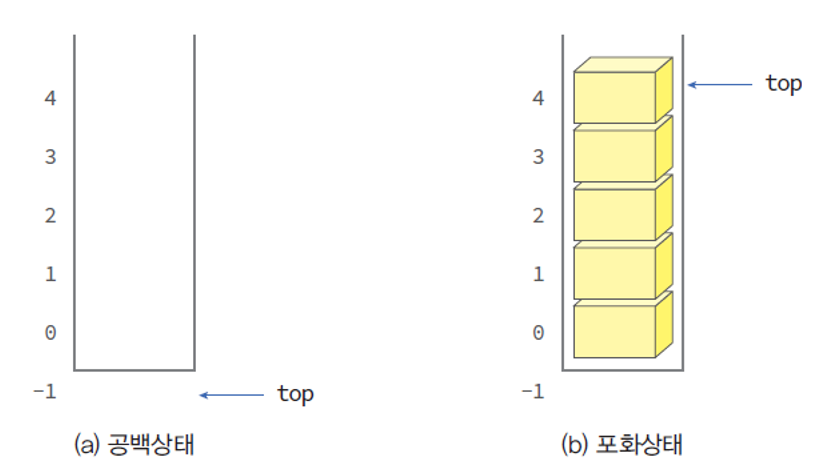
top 변수는 스택이 비어있으면 -1의 값을 가진다.

스택이 공백 상태일때 top이 0의 값을 가진다면,
stack[0]에 값이 있다는 것으로 해석이 되기 때문이다.

top 변수의 특성에 유의해 스택의 공백, 포화 상태 검사 함수를 의사코드로 알아보자.

is_empty , is_full 연산 함수의 구현

// top 변수가 -1이면 true, 그 외 false 를 반환함
// top 변수가 -1이 될 결우 더 이상의 pop() 은 불가능하다.
is_empty(S):
  if top == -1  // top 변수가 -1이 되는 순간 비로소 스택이 공백 상태가 됨에 유의하자 !!!
    then return TRUE 
    else return FALSE

// top 변수가 스택의 최대 크기보다 1이 작은 수 이면 true, 그 외 false 를 반환함.
// 배열은 0부터 index가 시작하므로 가장 마지막 요소의 index는 해당 배열의 크기보다 1이 작다.
// top 이 (MAX_STACK_SIZE-1) 이 되면 더 이상의 push() 는 불가능하다.
is_full(S): 
  if top == (MAX_STACK_SIZE-1)  // top 변수가 스택의 마지막 index를 가리키게 되면 stack이 포화상태가 된다.
    then return TRUE
    else return FALSE

스택 - 배열 : push() , pop() 연산

push() 연산 함수의 구현

push(S, x): // 스택 배열 구조체와 입력될 요소를 매개 변수로 넘긴다.

  if is_full(S) // 스택이 포화 상태이면 에러 발생
    then error "overflow" 
  else 
    top←top+1 // 요소 입력 전에 top 변수를 먼저 증가시키는 것에 유의하자.
              // top 변수를 먼저 증가시키지 않으면 기존의 top 위치에 새 요소가 덮어 씌어지게 된다.
    stack[top]←x // top 변수의 증가 후 요소의 입력이 실행된다.

pop() 연산 함수의 구현

pop(S, x): // 스택 배열 구조체와 삭제될 요소를 매개 변수로 넘긴다.

  if is_empty(S) // 스택이 공백 상태인 경우 에러 발생.
    then error "underflow" 
  else 
    e←stack[top] // 삭제될 공간(스택) 에 있던 요소를 보관 후
    top←top-1 // 배열의 크기를 줄여 스택을 삭제한다.
    return e  // 해당 공간에 있던 요소를 반환해준다.

동적 배열 스택 프로그램

이제 학습한 ADT와 함께 동적 배열 스택을 C언어로 구현해보자.

#include <stdio.h>
#include <stdlib.h>


typedef int element;

typedef struct {
  element *data;  // data는 포인터로 정의된다. (해당 스택(배열) 주소에 있는 값이기 때문에)
  int capacity; // 현재 크기
  int top;
} StackType;

// 스택 생성 함수
void init_stack(StackType *s) {
  s->top = -1;
  s->capacity = 1; // 하나의 요소가 들어오기 위한 여유 공간 확보
  s->data = (element *)malloc(s->capacity * sizeof(element)); // 동적 스택
}

// 스택 삭제 함수(동적 메모리 사용 후 메모리 반환)
void delete(StackType *s){
  free(s);
}

// 공백 상태 검출 함수
int is_empty(StackType *s) {
  return s->top == -1 ? 1 : 0;
}

// 포화 상태 검출 함수
int is_full(StackType *s) {
  return (s->capacity - 1) == s->top;
}


void push(StackType *s, element item) {
  if (is_full(s)) {

    // 동적 메모리 할당 (공간이 부족하면 메모리를 2배로 더 확보한다.)
    s->capacity *= 2;

    // realloc() 함수는 동적 메모리의 크기를 변경하는 함수로서, 현재 내용은 유지하면서 주어진 크기로 동적 메모리를 재할당한다.
    s->data = (element *)realloc(s->data, s->capacity * sizeof(element));
  }
  s->data[++(s->top)] = item; // top을 먼저 증가시켜 다음 공간을 지정한 후 item(요소) 를 넣는다.
}

// 삭제 함수
element pop(StackType *s) {
  if(is_empty(s)) {
    fprintf(stderr, "이미 비어있는 스택입니다.\n");
    exit(1);
  }
  else {
    // element e = s->data;
    // s->top = s->top - 1;
    // return e;

    return s->data[(s->top)--];
  }
}

int main(void) {
  StackType *s;

  s = (StackType *)malloc(sizeof(StackType));
  init_stack(s);

  push(s, 1);
	push(s, 2);
	push(s, 3);
	printf("%d\n", pop(s));
	printf("%d\n", pop(s));
	printf("%d\n", pop(s));

	free(s);
}

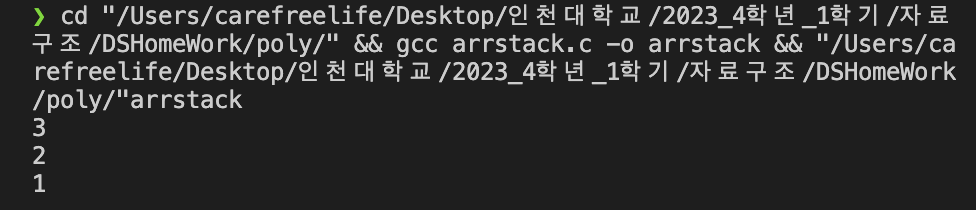
동적 배열 스택 프로그램 실행 결과

스택의 응용 1 : 괄호 검사

스택을 사용하여 괄호 검사 프로그램을 작성해보자.

스택을 사용하여 프로그램에 사용된 괄호의 쌍이 올바른지 검사하는 프로그램을 만들어보자.

조건:

왼쪽 괄호의 개수와 오른쪽 괄호의 개수가 같아야 한다.

같은 괄호에서 왼쪽 괄호는 오른쪽 괄호보다 먼저 나와야 한다.

괄호 사이에는 포함 관계만 존재한다.

괄호의 종류:
대괄호 (‘[’, ‘]’), 중괄호 (‘{’, ‘}’), 소괄호 (‘(’, ‘)’)

잘못된 괄호 사용의 예
(a(b)
a(b)c)
a{b(c[d]e}f)

괄호 검사 프로그램의 알고리즘

괄호 검사 프로그램의 알고리즘

알고리즘의 개요

괄호들은 가장 가까운 거리에 있는 괄호들끼리 서로 쌍을 이루어야 한다.

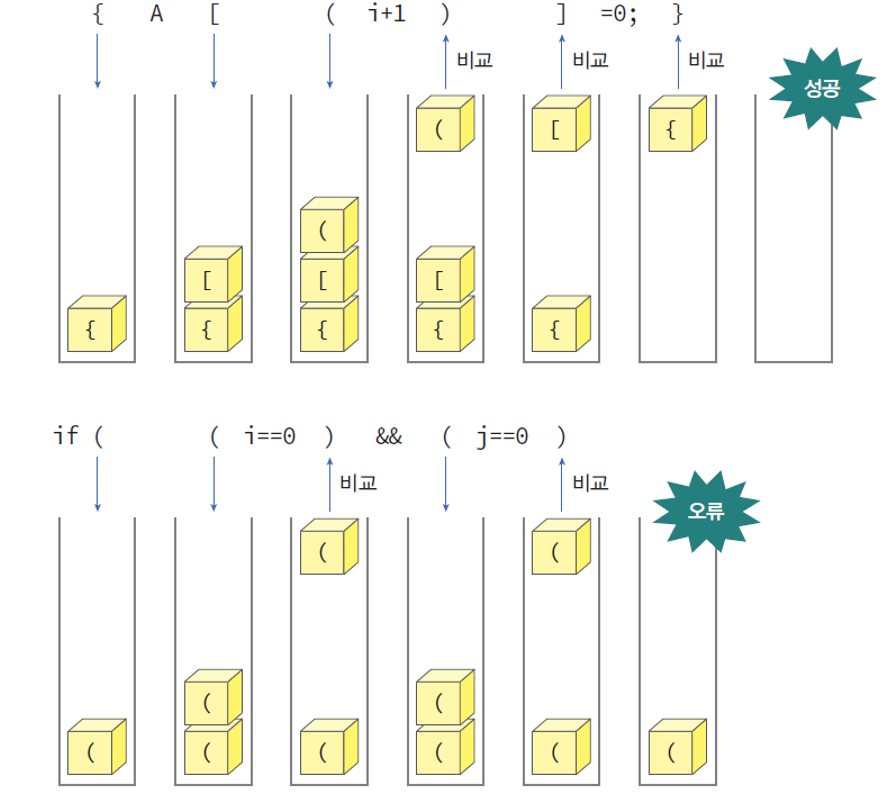
문자열에 저장되어 있는 괄호를 차례대로 조사하면서 왼쪽 괄호를 만나면 스택에 삽입(push)하고, 오른쪽 괄호를 만나면 스택에서 top괄호를 삭제(pop)한 후 오른쪽 괄호와 짝이 맞는지를 검사한다.

이때, 스택이 비어있으면 조건 1 또는 조건 2 위배. 괄호의 짝이 맞지 않으면 조건 3 등에 위배된다.

마지막 괄호까지 조사한 후에도 스택에 괄호가 남아 있으면 조건 1에 위배되므로 0(거짓)을 반환하고, 그렇지 않으면 1(참)을 반환한다.

괄호 검사 알고리즘을 pseudocode로 설계해보자.

check_matching(expr) :

while (입력 expr의 끝이 아니면) 
  ch ← expr의 다음 글자 
  switch(ch) 
    case '(': case '[': case '{': // 왼쪽 괄호 이면 스택에 삽입.
       ch를 스택에 삽입 
       break 
    case ')': case ']': case ']': // 오른쪽 괄호를 만나면 스택에서 pop후 두 괄호를 비교.
       if ( 스택이 비어 있으면 ) 
         then 오류 
       else 스택에서 open_ch를 꺼낸다 
           if (ch 와 open_ch가 같은 짝이 아니면) 
               then 오류 보고 
       break 
if( 스택이 비어 있지 않으면 ) 
  then 오류

이제 괄호 검사 프로그램을 이전에 작성한 pseudo code 를 바탕으로 구현해보자.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_STACK_SIZE 100

typedef char element; // 괄호가 들어갈 것이기 때문에 char 선언 할 것!

typedef struct {
    int top;
    element data[MAX_STACK_SIZE];
} StackType;

// 스택 생성
void init_stack(StackType *s) {
    s->top = -1;
}

// 메모리 반환
void delete(StackType *s) {
    free(s);
}

// 포화 상태 검사
int is_full(StackType *s) {
    return s->top == MAX_STACK_SIZE - 1;
}

// 공백 상태 검사
int is_empty(StackType *s) {
    return s->top == -1;
}
// 스택 추가
void push(StackType *s, element item) {
    if(is_full(s)) {
        fprintf(stderr, "스택이 포화 상태입니다.");
        exit(1);
    }
    else {
        s->data[++(s->top)] = item;
    }
}

// 스택 삭제
element pop(StackType *s) {
    if(is_empty(s)) {
        fprintf(stderr, "스택이 이미 공백 상태입니다.");
        exit(1);
    }
    else {
        return s->data[(s->top)--];
    }
}

// peek함수
element peek(StackType *s) {
    if(is_empty(s)) {
        fprintf(stderr, "스택이 공백 상태 입니다.");
        exit(1);
    }
    else {
        return s->data[s->top];
    }
}

int check_matching(const char *in) {
    StackType s;
    char ch, open_ch;
    int i, n = strlen(in); // n = 문자열의 길이
    
    init_stack(&s); // 스택의 생성, 초기화

    for(i = 0; i < n; i++) {
        
        ch = in[i]; // ch = 확인 대상인 문자열의 문자가 하나씩 들어온다.
        
        // switch 문으로 ch를 하나씩 검사한다. 
        switch (ch) {
            case '(': case '[': case '{': // 왼쪽 괄호이면 스택에 push,
                push(&s, ch);
                break;
            case ')': case ']': case '}': // 오른쪽 괄호이면 기존 스택의 데이터를 
                if(is_empty(&s)) {
                    return 0;
                }
                else {
                    open_ch = pop(&s); // pop()하여 open_ch 변수에 저장하고,
                    
                    // 기존 스택의 괄호(왼쪽 괄호, open_ch)와 새로 만난 오른쪽 괄호(ch)가 다르다면 종료. 
                    if ((open_ch == '(' && ch != ')') ||
                        (open_ch == '[' && ch != ']') ||
                        (open_ch == '{' && ch != '}')) {
                            return 0;
                        }
                    else break;
                }
        }
    }
    // 스택에 데이터가 하나라도 남아 있으면 오류.
    if(!is_empty(&s)) {
        printf("오류: 스택에 괄호가 남아있습니다.");
        return 0;
    }
    else return 1;
}

int main(void) {
    char *p = "{ A[(i+1)]=0; }";
    if (check_matching(p) == 1){
        printf("%s 괄호 검사 성공!\n ", p);
    }
    else {
        printf("%s 괄호 검사 실패...\n ", p);
    }
    return 0;
}

괄호 검사 프로그램 실행 결과

스택의 응용 2-1 : 후위 표기 수식의 계산

스택을 사용하여 후위 표기 수식 계산 프로그램을 작성해보자.

수식의 표기 방법:

전위(prefix) : 연산자가 피연산자 앞에 있다. (+1*2a)

중위(infix) : 연산자가 피연산자 사이에 있다. (1 + 2 * a)

후위(postfix) : 연산자가 피연산자 뒤에 있다. (12*+)
수식의 표기 방법

컴퓨터에서의 수식 계산 순서

프로그래머가 중위 표기식으로 작성한 수식을 컴파일러가 후위 표기식으로 변환 후에 계산한다.

중위 표기식 ▶️ 후위 표기식 ▶️ 계산 실행 (ex.) 2+34 ▶️ 234+ ▶️ 14

모두 스택을 사용한다.

후위 표기식 계산 알고리즘

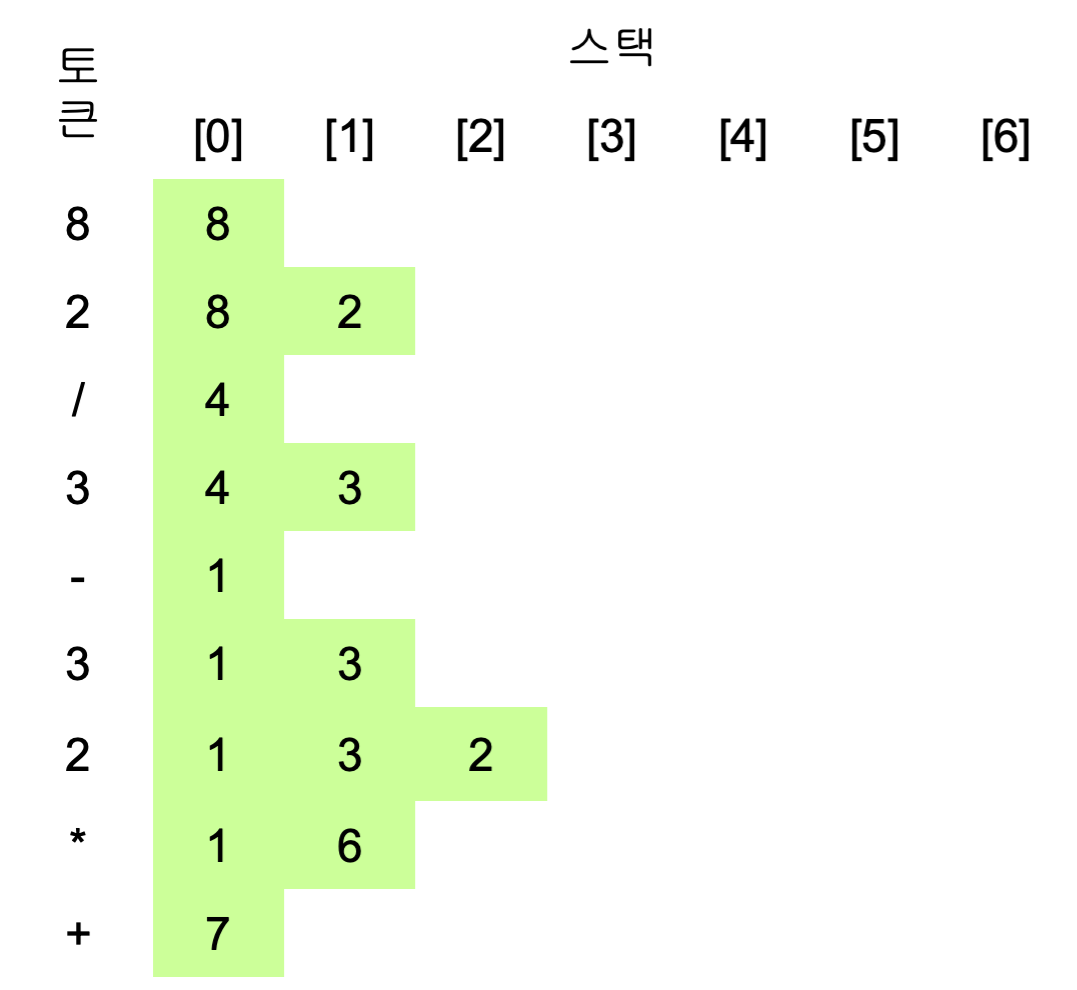
calpostfix_Procdess 후위 표기식의 계산 (82/3-32*+)

수식을 왼쪽에서 오른쪽으로 스캔 해나간다.
피연산자 이면 스택에 저장.
연산자를 만나는 순간 필요한 만큼의 피연산자를 스택에서 꺼내 연산을 실행하고, 그 결과를 다시 스택에 저장한다.
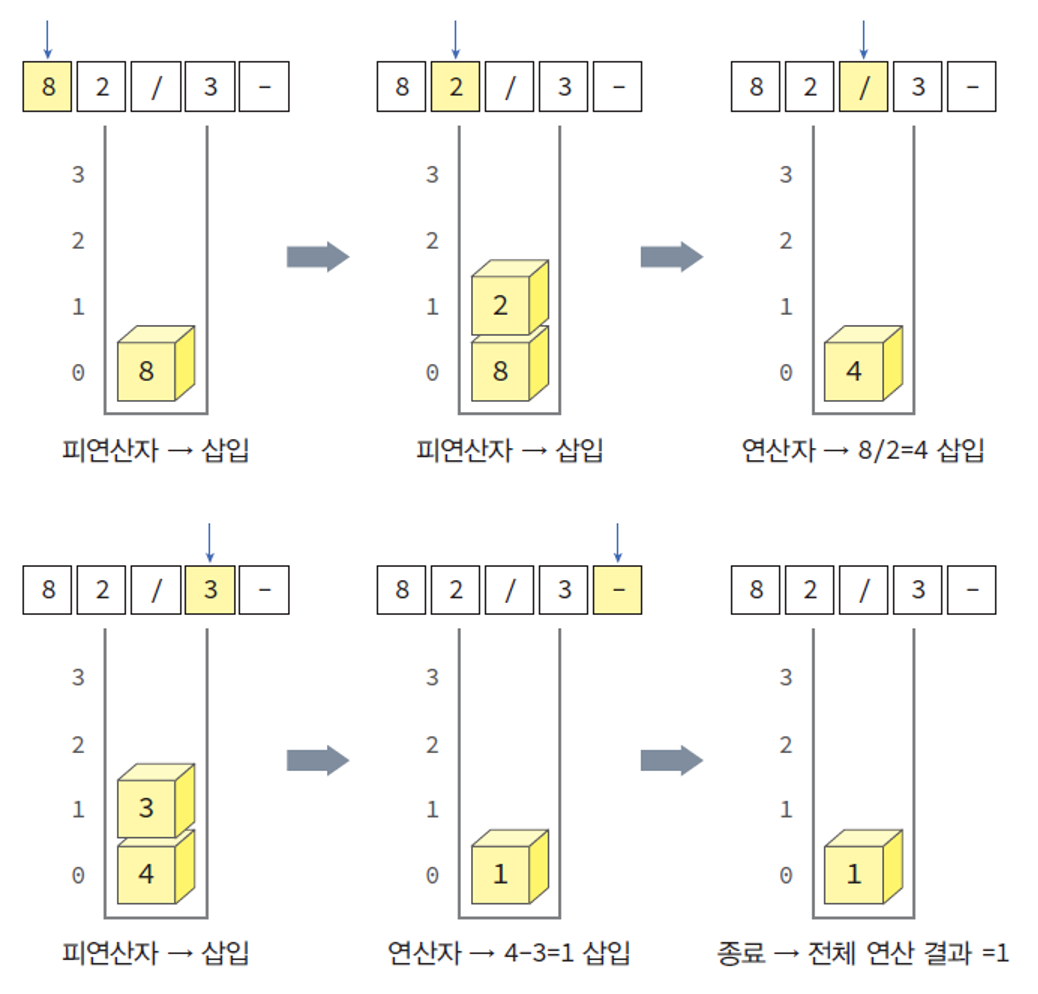
후위 표기식의 계산 과정 (82/3-32*+)

pseudo code

스택 s를 생성하고 초기화한다. 

for 항목 in 후위표기식 
  do if (항목이 피연산자이면) 
        push(s, item) 
     if (항목이 연산자 op이면) 
        then second ← pop(s) 
              first ← pop(s) 
              result ← first op second // op 는 +-*/중의 하나 
              push(s, result) 
final_result ← pop(s); 

C언어로 후위 표기 수식 계산 프로그램을 만들어보자.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_STACK_SIZE 100

typedef char element;

typedef struct {
    int top;
    element data[MAX_STACK_SIZE];
} StackType;

// 스택 초기화
void init_stack(StackType *s) {
    s->top = -1; 
}

// 스택 포화 검사
int is_full(StackType *s){
    return s->top == MAX_STACK_SIZE -1;
}
// 스택 공백 검사

int is_empty(StackType *s) {
    return s->top == -1;
}
// push()
void push(StackType *s, element item) {
    if(is_full(s)){
        fprintf(stderr, "error");
        exit(1);
    }
    s->data[++(s->top)] = item;
}
// pop()
element pop(StackType *s) {
    if(is_empty(s)) {
        fprintf(stderr, "error");
        exit(1);
    }
    return s->data[(s->top)--];
}
// peek()
element peek(StackType *s) {
    if(is_empty(s)) {
        fprintf(stderr, "error");
        exit(1);
    }
    return s->data[s->top];
}

// 후위 표기 수식 계산 함수
int eval(char exp[]) {
    int op1, op2, value, i = 0;
    int len = strlen(exp);
    char ch;
    StackType *s = (StackType *)malloc(sizeof(StackType));

    init_stack(s);

    for(i = 0; i<len; i++) {
        ch = exp[i]; // 매개변수로 넘어온 문자열 exp의 인덱스 0 부터 문자 하나를 꺼내 ch에 저장한다.
        if(ch != '+' && ch != '-' && ch != '*' && ch != '/') {
            value = ch - '0'; // ?
            push(s, value);
        }
        else {  // 연산자이면 피연산자를 스택에서 제거.
            op2 = pop(s);
            op1 = pop(s);
            switch(ch) {
                case '+': push(s, op1 + op2); break;
                case '-': push(s, op1 - op2); break;
                case '*': push(s, op1 * op2); break;
                case '/': push(s, op1 / op2); break;
            }
        }
    }
    return pop(s); // 모든 연산이 끝나고 남은 결과를 pop 반환
}

int main(void) {
    int result;
    printf("후위 표기식은 82/3-32*+\n");
    result = eval("82/3-32*+");
    printf("결과값은 %d", result);
    return 0;
}

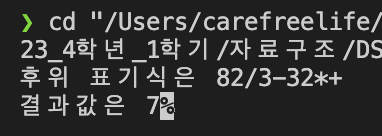
후위 표기식 프로그램의 실행 결과 (82/3-32*+)

스택의 응용 2-2 : 중위 표기식을 후위 표기식으로 변환

중위 표기식을 후위 표기식으로 변환해보자.

후위 표기식 프로그램의 실행 결과 (82/3-32*+)

기본적으로 프로그래머는 중위 표기식으로 연산을 표현하며, 컴퓨터는 후위 표기식으로 연산을 실행한다.

따라서 우리는 중위 표기식을 후위 표기식으로 변환해줄 필요가 있다.

중위 표기법과 후위 표기법의 공통점은 피연산자의 순서가 동일하다는 것.

연산자의 순서는 우선 순위 순서로 다르다.

연산자만 스택에 저장 후 출력하면 된다.

(ex.) 2+34 ▶️ 234+

위 내용을 바탕으로 pseudo code를 작성해보자.

infix_to_postfix(exp) :

스택 s를 생성하고 초기화 
while (exp에 처리할 문자가 남아 있으면) 
     ch ← 다음에 처리할 문자 
     switch (ch) 
       case 연산자: 
         while ( peek(s)의 우선순위 ≥ ch의 우선순위 ) 
           do e ← pop(s) 
              e를 출력             
         push(s, ch); 
         break; 
       case 왼쪽 괄호:      
         push(s, ch); 
         break; 
       case 오른쪽 괄호: 
         e ← pop(s); 
         while( e ≠ 왼쪽괄호 ) 
           do e를 출력 
              e ← pop(s) 
         break; 
       case 피연산자: 
         ch를 출력 
         break;

while( not is_empty(s) )  
      do e ← pop(s) 
         e를 출력

C언어로 구현한 
중위 표기 수식을 후위 표기 수식으로 변환하는 프로그램

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_STACK_SIZE 100

typedef char element;

typedef struct {
    int top;
    element data[MAX_STACK_SIZE];
} StackType;

// 스택 초기화
void init_stack(StackType *s) {
    s->top = -1; 
}

// 스택 포화 검사
int is_full(StackType *s){
    return s->top == MAX_STACK_SIZE -1;
}
// 스택 공백 검사

int is_empty(StackType *s) {
    return (s->top == -1);
}
// push()
void push(StackType *s, element item) {
    if(is_full(s)){
        fprintf(stderr, "push error");
        exit(1);
    }
    else s->data[++(s->top)] = item;
}
// pop()
element pop(StackType *s) {
    if(is_empty(s)) {
        fprintf(stderr, "pop error");
        exit(1);
    }
    else return s->data[(s->top)--];
}
// peek()
element peek(StackType *s) {
    if(is_empty(s)) {
        fprintf(stderr, "peek error");
        exit(1);
    }
    return s->data[s->top];
}

// 연산자의 우선순위를 반환한다.
int prec(char op) {
    switch(op) {
        // 왼쪽 괄호는 보이는 순간 무조건 스택에 삽입하며,
        // 왼쪽 괄호는 스택에 삽입되는 순간 가장 우선순위가 낮은 연산자로 취급된다.
        // 즉 왼쪽괄호 이후 연산자들은 스택에 모두 삽입되며 
        // 오른쪽 괄호를 만나게되면 스택에 쌓여있는 연산자들을 왼쪽 괄호가 삭제될 때까지 출력한다.
        case '(': case ')': return 0;
        case '+': case '-': return 1;           
        case '*': case '/': return 2;
    }
    return -1;
}

// 중위 표기 수식을 후위 표기 수식으로 변환하는 프로그램.
void infix_to_postfix(char exp[]) {
    int i = 0;
    char ch, top_op;
    int len = strlen(exp);
    StackType *s = (StackType *)malloc(sizeof(StackType));

    // 스택 초기화
    init_stack(s);

    for(i = 0; i<len; i++) {
        
        ch = exp[i];

        switch (ch) {
        // 연산자
        case '+': case '-': case '*': case '/': 
            // 스택에 있는 연산자의 우선순위가 더 크거나 같으면 출력
            while (!is_empty(s) && (prec(ch) <= prec(peek(s)))) {
                printf("%c", pop(s));
            }
            push(s, ch);
            break;
        // 왼쪽 괄호 - 무조건 삽입.
        case '(':
            push(s, ch);
            break;
        // 오른쪽 괄호 
        case ')':
            top_op = pop(s);
            // 왼쪽 괄호를 만날때까지 출력
            while(top_op != '(') {
                printf("%c", top_op);
                top_op = pop(s);
            }
            break;
        // 피연산자 (default : case 에 속하지 않는 것들)
        default:
            printf("%c", ch);
            break;
        }
    }
    // 스택에 저장된 연산자들 출력
    while (!is_empty(s)) {
        printf("%c", pop(s));
    }
}

int main(void) {
	char *s = "(2+3)*4+9";
	printf("중위표시수식 %s \n", s);
	printf("후위표시수식 ");
	infix_to_postfix(s);
	printf("\n");
	return 0;
}

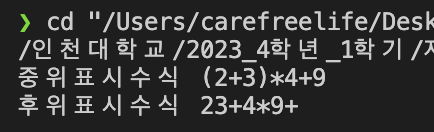
후위 표기식 변환 프로그램의 실행 결과 (2+3)*4+9

스택의 응용 3 : 미로 문제 (Maze Solving Problem)

이제 스택의 마지막 예제이다.

미로를 탈출하는 방법을 스택을 이용해 찾아보자.

사진출처Maze

미로의 출구를 찾는 방법 중 가장 기본적인 방법은 시행착오 방법이다.

시행착오 방법: 하나의 경로를 선택하여 한번 시도해보고 안되면 다시 다른 경로를 시도.

막다른 길에 도달 시 해당 위치에서 가장 가까웠던 다른 경로를 찾아야 한다.

해당 위치에서 가장 가까운 다른 경로란, 가장 최근에 저장된 다른 경로이다.

가장 최근에 저장한 경로를 쉽게 추출할 수 있는 자료구조에는 스택(Stack)이 적합.

문제 해결의 순서
현재 위치에서 갈 수 있는 방들의 좌표를 스택에 저장.
- 위, 아래, 왼쪽, 오른쪽 순서로 스택에 저장.
- 스택의 top에 저장된 위치를 자신의 위치로 대치.
- 현재 위치가 출구의 위치와 같거나 모든 위치를 다 검사할 때까지 반복.
- 한번 거쳐간 위치를 다시 검사하지 않도록 지나간 경로에는 표시.

막다른 길 도달시 가장 최근에 저장된 가능 경로로 이동.
한번 지나간 방은 지나가지 않기 위해 방문했다는 표시를 한다.

미로 탐색 알고리즘
스택 s과 출구의 위치 x, 현재 생쥐의 위치를 초기화 
while( 현재의 위치가 출구가 아니면 ) 
  do  현재위치를 방문한 것으로 표기 
      if( 현재위치의 위, 아래, 왼쪽, 오른쪽 위치가 아직 방문되지 않았고 갈수 있으면 ) 
        then 그 위치들을 스택에 push 
      if( is_empty(s) ) 
         then 실패 
         else 스택에서 하나의 위치를 꺼내어 현재 위치로 만든다; 
성공; 

C언어로 미로 탐색 프로그램을 구현해보자.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>


#define MAZE_SIZE 6 // 미로의 크기는 6 X 6
#define MAX_STACK_SIZE 100

// typedef char element;
// 이전 예제에서 사용한 chat형 element를 struct 형 element로 바꿔줘야 한다.
typedef struct {
    short r;
    short c;
} element;

typedef struct {
    int top;
    element data[MAX_STACK_SIZE];
}StackType;



// 스택 초기화
void init_stack(StackType *s) {
    s->top = -1;
}

// 스택 포화 검사
int is_full(StackType *s){
    return s->top == MAX_STACK_SIZE -1;
}
// 스택 공백 검사

int is_empty(StackType *s) {
    return s->top == -1;
}
// push()
void push(StackType *s, element item) {
    if(is_full(s)){
        fprintf(stderr, "error");
        exit(1);
    }
    s->data[++(s->top)] = item;
}
// pop()
element pop(StackType *s) {
    if(is_empty(s)) {
        fprintf(stderr, "error");
        exit(1);
    }
    return s->data[(s->top)--];
}
// peek()
element peek(StackType *s) {
    if(is_empty(s)) {
        fprintf(stderr, "error");
        exit(1);
    }
    return s->data[s->top];
}


// 1은 벽, 0은 위치 가능한 좌표
// e 는 시작점, x 는 출구이다.
char maze[MAZE_SIZE][MAZE_SIZE] = {
	{ '1', '1', '1', '1', '1', '1' },
    { 'e', '0', '1', '0', '0', '1' },
    { '1', '0', '0', '0', '1', '1' },
    { '1', '0', '1', '0', '1', '1' },
    { '1', '0', '1', '0', '0', 'x' },
    { '1', '1', '1', '1', '1', '1' },
};

//위치를 스택에 삽입
void push_loc(StackType *s, int r, int c) {
    
    if(r < 0 || c < 0) return;
    
    // 벽을 표현하는 1과 한번 지나간 위치인 . 이 아니면 실행
    if(maze[r][c] != '1' && maze[r][c] != '.') {
        element tmp;
        //element 구조체에 매개변수로 넘어온 row 와 column 값을 넣어준다
        tmp.r = r;
        tmp.c = c;

        // 이동 가능한 위치 값이 들어간 구조체 element를 stack에 넣어준다.
        push(s, tmp);
    }
}

void maze_print(char maze[MAZE_SIZE][MAZE_SIZE]) {
    printf("\n");
    for (int r = 0; r < MAZE_SIZE; r++) {
        for(int c = 0; c < MAZE_SIZE; c++) {
            printf("%c", maze[r][c]);
        }
        printf("\n");
    }
}

// 현재 위치, 시작점
element here = {1, 0}, entry = {1, 0};

int main(void) {
    int r, c;
    StackType *s = (StackType *)malloc(sizeof(StackType));

    //스택 초기화
    init_stack(s);

    //위치를 나타내는 element 구조체 초기화 (시작점 entry로 이동)
    here = entry;

    // x에 도달할때까지 반복
    while(maze[here.r][here.c] != 'x') {
        r = here.r;
        c = here.c;

        // 지나간 곳 . 표시
        maze[r][c] = '.';

        maze_print(maze);

        // 동서남북을 push_loc 통해 탐색. (push_loc 내부에서 가능한 경로 선정하여 스택에 push함)
        // 상, 하, 좌, 우 순으로 stack에 push.
        push_loc(s, r-1, c);  // 위
        push_loc(s, r+1, c);  // 아래
        push_loc(s, r, c-1);  // 왼쪽
        push_loc(s, r, c+1);  // 오른쪽

        // x에 도착하기전에 가능한 경로가 쌓여있는 stack이 공백상태이면 실패.
        if(is_empty(s)) {
            printf("실패\n");
            return 0;
        }
        // push_loc이 stack에 push한 가능한 경로 중 가장 최근에 입력한 (가까운) 위치를 찾아 pop()하여 이동.
        else {
            here = pop(s);
        }
    }
    printf("성공\n");
    return 0;
}

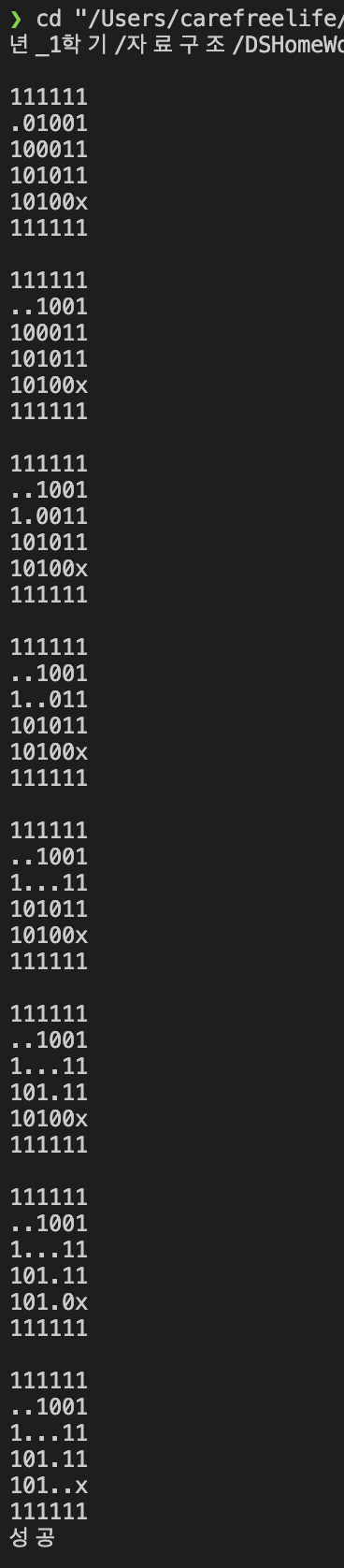
미로 탐색 프로그램의 실행 결과

최대한의 설명을 코드 블럭 내의 주석으로 달아 놓았습니다.

혹시 이해가 안가거나 추가적인 설명이 필요한 부분, 오류 등의 피드백은 언제든지 환영합니다!

긴 글 읽어주셔서 감사합니다. 스택 (Stack) 포스팅을 마칩니다.

처음으로~

참고: C언어로 쉽게 풀어쓴 자료구조 <개정 3판> 천인국, 공용해, 하상국 지음

Task Lists

Data Structure : 스택 (Stack) 이란?

스택의 특징, 스택의 구조, 스택의 추상 데이터 타입(ADT), 스택의 연산

시스템 스택을 이용한 함수 호출

배열을 이용해 스택을 구현

동적 배열 스택 프로그램

스택의 응용 1 : 괄호 검사

스택의 응용 2-1 : 후위 표기 수식의 계산

스택의 응용 2-2 : 중위 표기식을 후위 표기식으로 변환

스택의 응용 3 : 미로 문제 (Maze Solving Problem)

Twitter Facebook LinkedIn

Chae Seungmin

Data Structure : (5) 스택(Stack)

Data Structure :: 스택 (Stack)

스택의 구현

스택의 구현 : 배열

동적 배열 스택 프로그램

스택의 응용 1 : 괄호 검사

스택의 응용 2-1 : 후위 표기 수식의 계산

스택의 응용 2-2 : 중위 표기식을 후위 표기식으로 변환

스택의 응용 3 : 미로 문제 (Maze Solving Problem)

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)

※블로그 이전 안내※

Chae Seungmin

Data Structure :: 스택 (Stack)

스택의 구현

스택의 구현 : 배열

동적 배열 스택 프로그램

스택의 응용 1 : 괄호 검사

스택의 응용 2-1 : 후위 표기 수식의 계산

스택의 응용 2-2 : 중위 표기식을 후위 표기식으로 변환

스택의 응용 3 : 미로 문제 (Maze Solving Problem)

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)