Data Structure - 그래프 (Graph) (2) - Kruskal VS Prim

8 minute read

신장 트리 (Spanning Tree) 란?

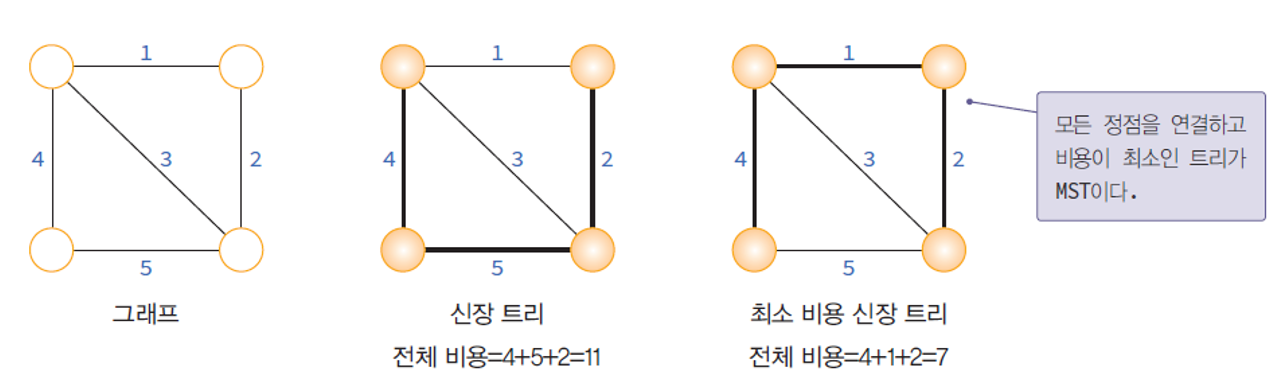
신장 트리의 모습

신장 트리(Spanning Tree) : 그래프 내의 모든 정점을 포함하는 트리.

트리(Tree)의 특수한 형태이다.

모든 정점들이 연결되어 있어야 하며 동시에 사이클(Cycle)을 포함해서는 안된다.

따라서 신장 트리는 그래프에 있는 n개의 정점을 정확히 n - 1 개의 간선으로 연결하게 된다.

하나의 그래프에는 여러 개의 신장 트리가 존재 가능하다.

깊이 우선 탐색(DFS)이나 너비 우선 탐색(BFS) 도중에 사용된 간선을 모아 표시하면 만들 수 있다.

신장 트리는 그래프의 최소 연결 부분 그래프가 된다.

// 신장 트리의 알고리즘 (pseudo code)
depth_first_search(v):
    v를 방문 되었다고 표시;
    for all u ⍷ (v에 인접한 정점) do
        if(u가 아직 방문되지 않았으면)
            then (v, u)를 신장 트리 간선이라고 표시;
                depth_first_search(u)

최소 비용 신장 트리 (MST : Minimum Spanning Tree) 란?

최소 비용 신장 트리 : 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 신장 트리.
최소 신장 트리의 모습

네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결.

MST의 응용

도로 건설, 전기 회로, 통신, 배관

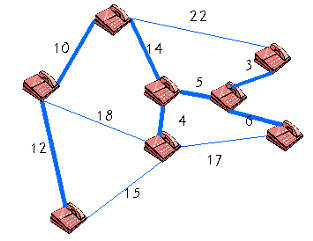
최소 신장 트리의 예

Kruskal 의 MST 알고리즘

Kruskal Algorithm은 탐욕적인 방법(Greedy method)을 사용한다.

Greedy Method(탐욕적인 방법)

주요 알고리즘 설계 기법

각 단계에서의 최선책을 선택하는 과정을 반복하여 최종적인 해답에 도달.

탐욕적인 방법은 항상 최적의 해답을 주는지 검증 필요.

Kruskal MST Algorithm은 최적의 해답임이 증명되어 있다.

// Kruskal의 MST 알고리즘 (pseudo code)

// 입력: 가중치 그래프 G = (V, E), n은 노드의 개수.
// 출력: E_T, 최소 비용 신장 트리를 이루는 간선들의 집합.
kruskal(G)
    E를 w(e_1) <= ... <= w(e_e) 가 되도록 정렬.
    E_T ← ⏀; ecounter ← 0
    k ← 0
    while ecounter < (n-1) do
        k ← k + 1
        if(E_T U {e_k} 가 사이클을 포함하지 않으면
            then E_T ← E_T U {e_k}; ecounter ← ecounter + 1
    return E_T 

Kruskal 알고리즘

MST가 최소 비용의 간선(n-1)으로 구성됨과 동시에 사이클을 포함하하지 않는다는 조건에 근거

각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택.

그래프의 간선들을 가중치의 오름차순으로 정렬.

정렬된 간선의 리스트에서 사이클을 형성하지 않는 간선을 탐색.

만약 해당 간선이 사이클을 형성한다면 PASS 한다.

해당 간선이 이미 다른 경로에 의해 연결되어 있는 정점들을 연결할 때 사이클이 형성된다.

현재까지의 MST의 집합에 해당 간선을 추가.

위 과정을 간선의 개수가 정점의 개수보다 하나 작을 때까지 반복한다. (간선의 개수 : n-1)

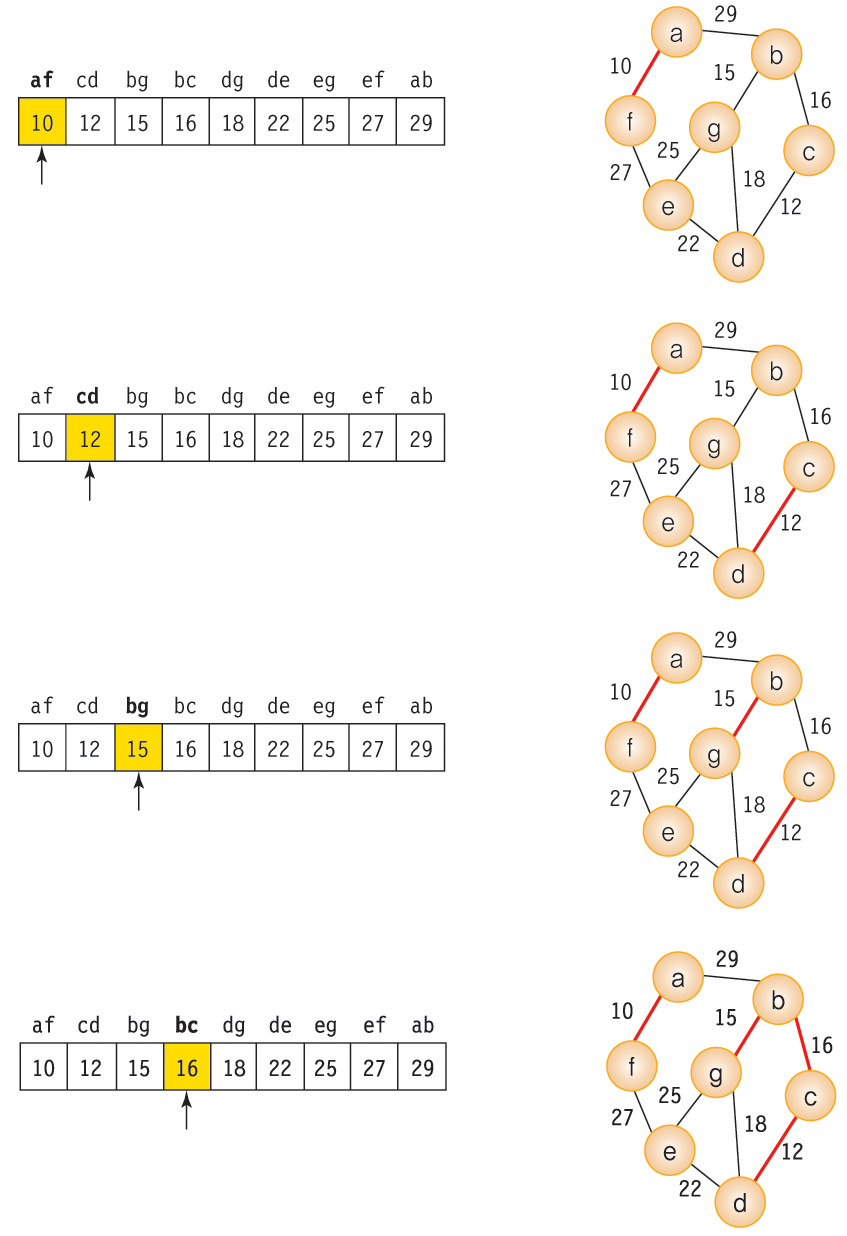
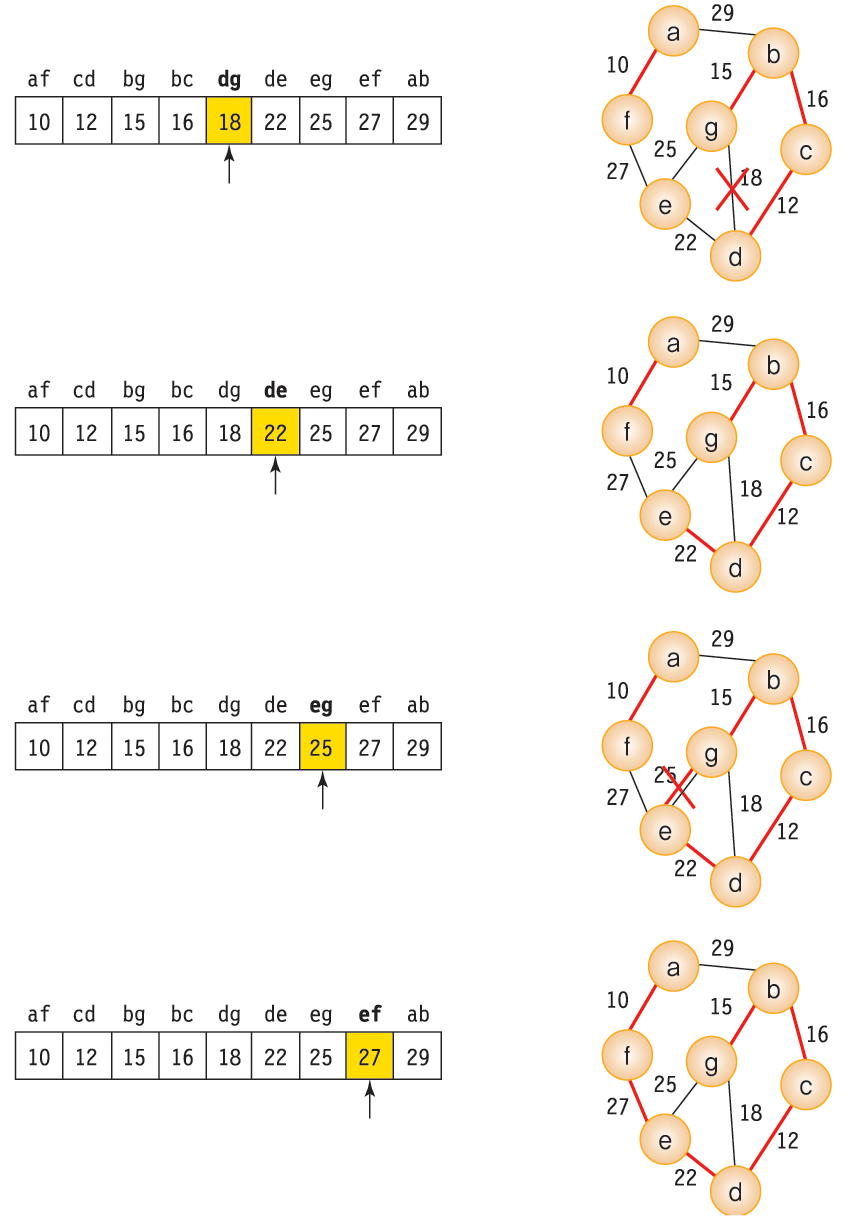
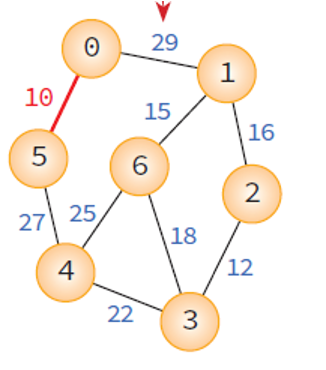
Kruskal Algorithm 의 과정

(Kruskal) union - find 연산

union(x, y) 연산은 원소 x와 y가 속해 있는 집합을 입력으로 받아 2개 집합의 합집합을 반환.

find(x, y) 연산은 원소 x가 속해있는 집합을 반환한다.

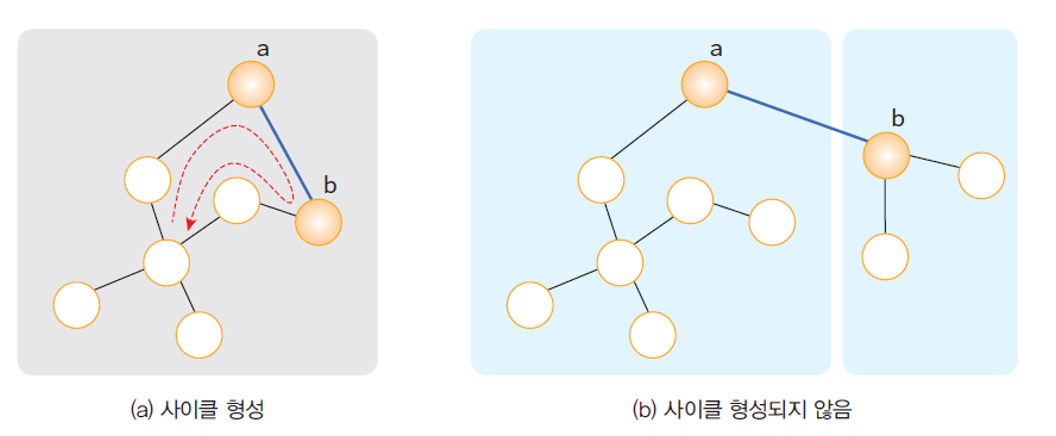
union-find : 그림(a) a와 b가 같은 집합에 속함 / 그림(b) a와 b가 다른 집합에 속함

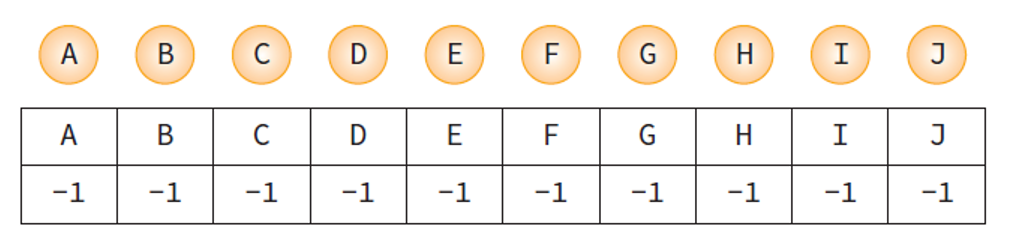
초기 모습. 처음엔 모든 노드들이 분리되어 있고 parent 배열은 -1 로 초기화 되어 있다.

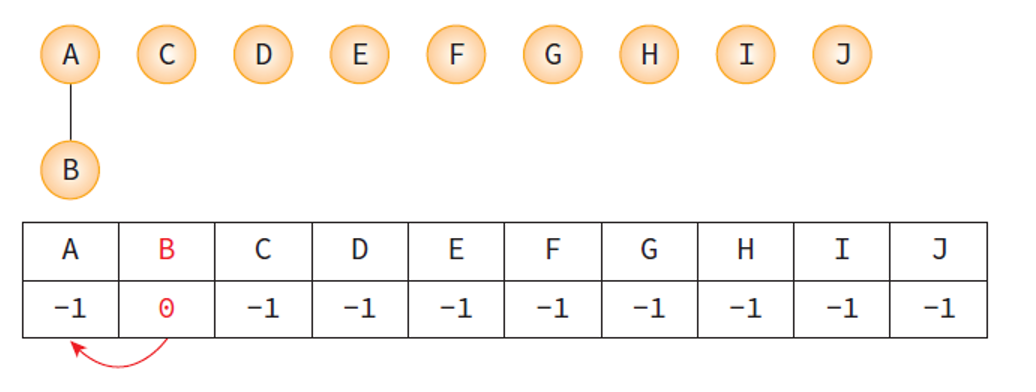
union(A, B) 실행 후 모습.

B는 A와 합쳐졌기 때문에 A의 인덱스인 0이 B의 자리에 저장된다.

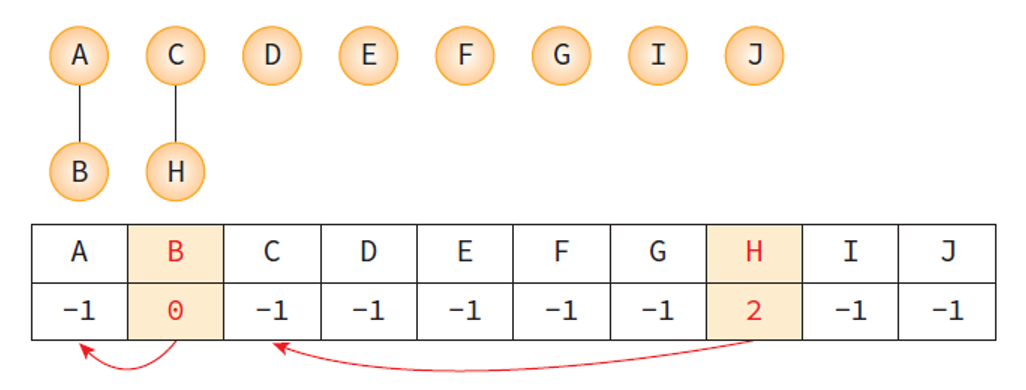
union(C, H) 실행 후 모습.

H는 C와 합쳐졌기 때문에 C의 인덱스인 2가 H의 자리에 저장된다.

union - find 알고리즘 (pseudo code)

UNION(a, b):
    root1 = FIND(a); // 노드 a의 루트를 찾는다.
    root2 = FIND(b); // 노드 b의 루트를 찾는다.
    if root1 != root2 // 두 노드의 루트 노드가 같지 않으면 합한다.
        parent[root1] = root2;
        
FIND(curr): // curr의 루트를 찾는다.
    // parent 배열에는 각 노드들의 루트 노드가 저장되어 있다.
    // 만약 -1(초기화 값)인 경우에는 부모 노드가 없는 것이므로 curr을 반환한다.
    if(parent[curr] == -1) 
        return curr;
    while(parent[curr] != -1) curr = parent[curr]; // 초기화 값이 나올 때까지 부모 노드를 찾아 이동.
    return curr;

전체 Kruskal 알고리즘을 C코드로 구현 해보자.

#include<stdio.h>
#include<stdlib.h>

#define TRUE 1
#define FALSE 0

#define MAX_VERTICES 7
#define INF 1000

int parent[MAX_VERTICES]; // 부모 노드

// 부모 노드 초기화
void set_init(int n){
    for(int i = 0; i < n; i++){
        parent[i] = -1;
    }
}

// curr가 속하는 집합을 반환
int set_find(int curr){
    // parent 배열에는 각 노드들의 루트 노드가 저장되어 있다.
    // 만약 -1(초기화 값)인 경우에는 부모 노드가 없는 것이므로 curr을 반환한다.
    if(parent[curr] == -1){
        return curr;
    }
    while(parent[curr] != -1){
        curr = parent[curr]; // 초기화 값이 나올 때까지 부모 노드를 찾아 이동.
    }
    return curr;
}

// 두 개의 원소가 속한 집합을 합친다.
void set_union(int a, int b){
    int root1 = set_find(a);
    int root2 = set_find(b);

    if(root1 != root2){
        parent[root1] = root2;
    }
}

// 간선을 나타내는 구조체
struct Edge{
    int start, end, weight;
};

typedef struct GraphType {
    int n; // 정점의 개수
    struct Edge edges[2 * MAX_VERTICES];
} GraphType;

// 그래프 초기화
void init_graph(GraphType *g){
    g->n = 0;
    for(int i = 0; i < 2 * MAX_VERTICES; i++){
        g->edges[i].start = 0;
        g->edges[i].end = 0;
        g->edges[i].weight = INF; // 초기화 시 모든 간선의 가중치는 무한대.
    }
}

// 간선 삽입 연산
void insert_edge(GraphType *g, int start, int end, int weight){
    g->edges[g->n].start = start;
    g->edges[g->n].end = end;
    g->edges[g->n].weight = weight;
    g->n++;
}

// qsort()에 사용되는 함수
int compare(const void* a, const void* b){
    struct Edge* x = (struct Edge*)a;
    struct Edge* y = (struct Edge*)b;
    return (x->weight - y->weight);
}

// kruskal의 최소 비용 신장 트리 프로그램
void kruskal(GraphType *g){
    int edge_accepted = 0;
    int uset, vset; // 정점 u와 정점 v의 집합 번호
    struct Edge e;

    set_init(g->n);
    qsort(g->edges, g->n, sizeof(struct Edge), compare);

    printf("크루스칼 최소 신장 트리 알고리즘\n");
    int i = 0;
    while(edge_accepted < MAX_VERTICES - 1){  // 결과 간선의 수 < (n-1)
        e = g->edges[i];
        uset = set_find(e.start); // 정점 u의 집합 번호
        vset = set_find(e.end); // 정점 v의 집합 번호

        if (uset != vset){  // 서로 속한 집합이 다르면
            printf("간선 (%d, %d) %d 선택 \n", e.start, e.end, e.weight);
            edge_accepted++;
            set_union(uset, vset); // 두 집합을 합친다.
        }
        i++;
    }
}

int main(void)
{
	GraphType *g;
	g = (GraphType *)malloc(sizeof(GraphType));
	init_graph(g);

	insert_edge(g, 0, 1, 29);
	insert_edge(g, 1, 2, 16);
	insert_edge(g, 2, 3, 12);
	insert_edge(g, 3, 4, 22);
	insert_edge(g, 4, 5, 27);
	insert_edge(g, 5, 0, 10);
	insert_edge(g, 6, 1, 15);
	insert_edge(g, 6, 3, 18);
	insert_edge(g, 6, 4, 25);

	kruskal(g);
	free(g);
	return 0;
}

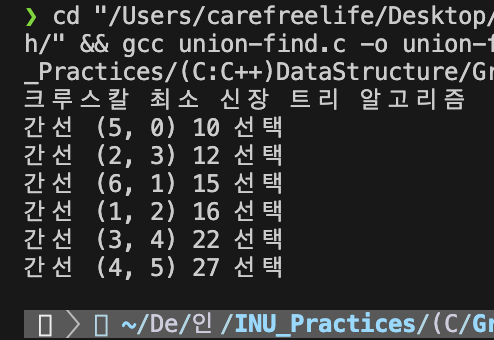
Kruskal 알고리즘 실행 결과

Kruskal 알고리즘의 시간 복잡도 분석

union-find 알고리즘을 이용하면 kruskal의 알고리즘의 시간 복잡도는 간선들을 정렬하는 시간에 좌우됨.

효율적인 정렬 알고리즘을 사용한다면 kruskal 알고리즘의 시간복잡도는
e * log_2 e 이다.

Prim 의 MST 알고리즘

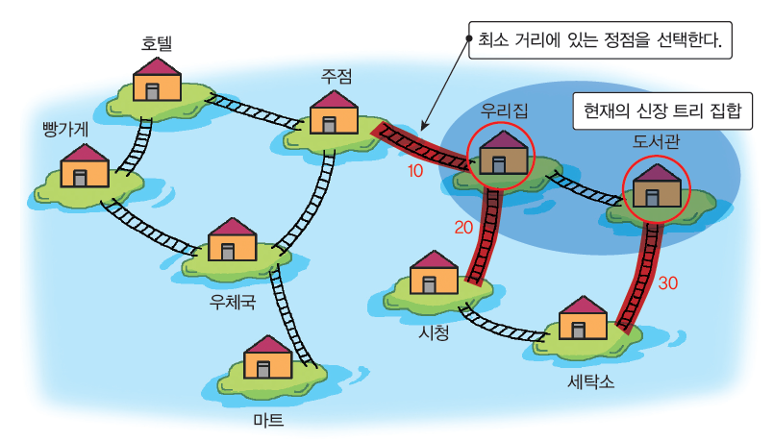
Prim's MST Algorithm
시작 정점에서부터 출발하여 신장 트리 집합을 단계적으로 확장해나가는 방법

시작 정점을 신장 트리 집합에 추가하여 시작한다.

앞 단계에서 만들어진 신장 트리 집합에 인접 정점 중 최저 가중치의 간선으로 연결된 정점을 선택 및 추가하여 트리를 확장.

트리가 n - 1개의 간선을 가질 때까지 반복.

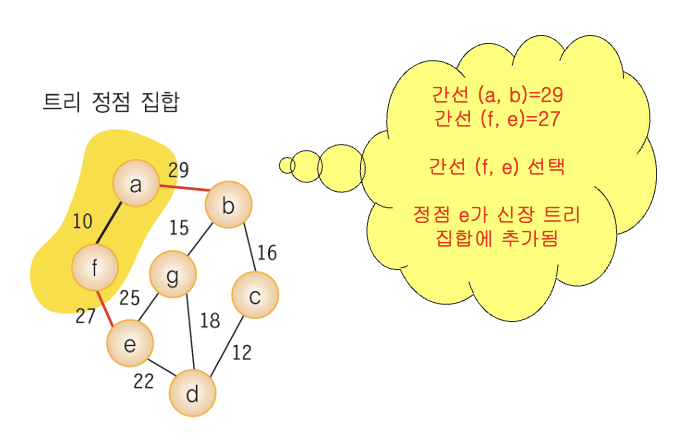
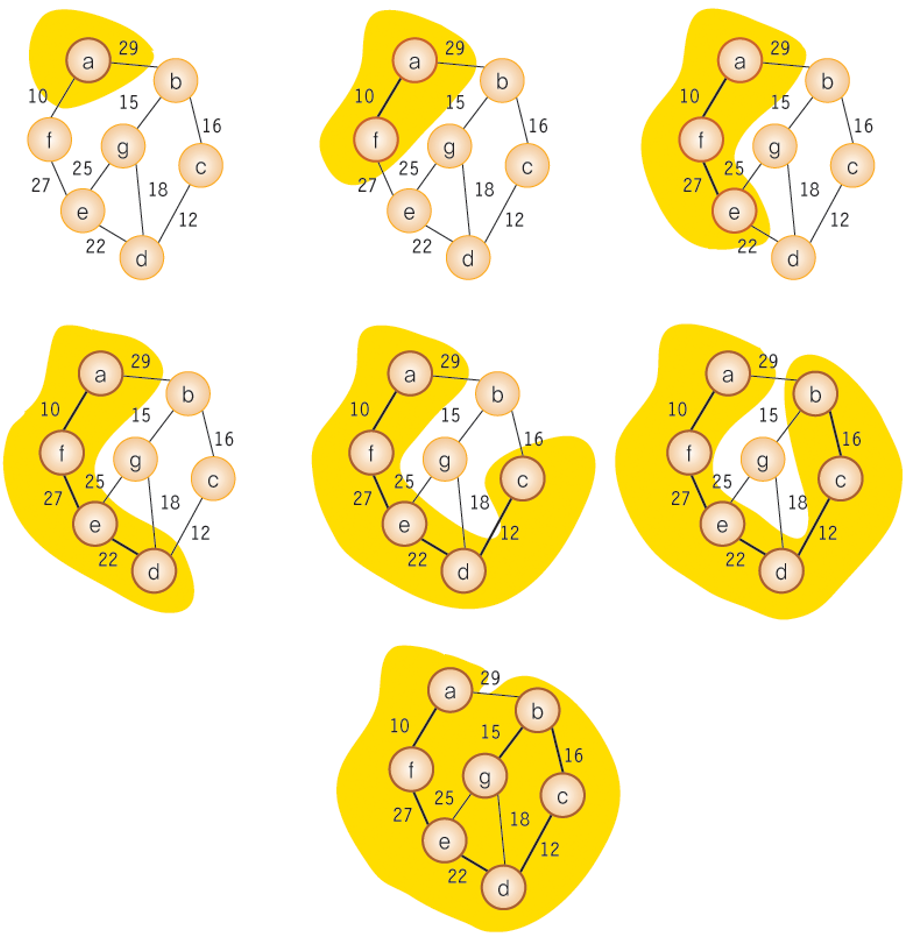
Prim 알고리즘의 동작 과정

정점 a에서 출발. - 신장 트리 집합 : {a}

a의 인접 정점 중 최저 가중치 간선을 선택 (a, f) - 신장 트리 집합 : {a, f}

신장 트리 집합에 인접한 정점은 b, e 해당 간선의 가중치에 따라 (f, e)간선 선택. - 신장 트리 집합 : {a, f, e}

위 과정을 신장 트리 집합의 정점 개수가 n - 1 개가 될 때까지 반복.

Prim의 MST 알고리즘 (pseudo code)

// Prim의 MST 알고리즘
// 입력: 네트워크 G=(V, E), S는 시작 정점
// 출력: V_T, MST를 이루는 정점들의 집합

// distance[] 는 현재까지 알려진, 신장 트리 정점 집합에서 각 정점까지의 거리를 가지고 있다.
//  - 처음에는 시작 노드만 값이 0 이고 다른 노드는 전부 무한대의 값을 가진다. (아직 알려지지 않았으므로)

Prim(G, s):
    for each u ⍷ V do
        distance[u] ← ⚭ // 각 정점과의 거리 초기화.
    distance[s] = 0; // 시작 노드와의 거리는 0
    우선 순위 큐 Q에 모든 정점을 삽입 (우선 순위는 dist[])
    for i ← 0 to n - 1 do
        u ← delete_min(Q)
        화면에 u를 출력
        for each v ⍷ (u의 인접 정점)
            if(v ⍷ Q and weight[u][v] < dist[v])
                then dist[v] ← weight[u][v] 

정점들이 트리 집합에 추가되면서 distance 값은 변경된다.

우선 순위 큐에 모든 정점을 삽입한다. 이때의 우선 순위는 distance 배열 값이 된다.

while 루프로 우선 큐에서 가장 작은 distance 값을 가진 정점을 꺼낸다.

바로 이 정점이 트리 집합에 추가된다.

트리 집합에 새로운 정점인 u 가 추가 되었으므로 u에 인접한 정점v 들의 distance 값을 갱신해준다.

기존의 distance[v] 값보다 간선(u, v)의 가중치 값이 적으면 간선 (u, v)의 가중치 값으로 distance를 변경시킨다. 5. Q에 있는 모든 정점들이 소진 될 때까지 위의 과정을 반복한다. (is_empty)

한번 선택된 정점은 Q에서 dequeue 되는 것이므로 삭제된다.

트리 집합에 인접하지 않은 정점들의 dist 값은 무한대이므로 선택되지 않는다.

만약 선택된 정점의 값이 무한대이면 오류인 것.

전체 Prim 알고리즘을 C코드로 구현 해보자.

// Prim 알고리즘
#include<stdio.h>
#include<stdlib.h>

#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000L

typedef struct GraphType {
    int n; // 정점의 개수
    int weight[MAX_VERTICES][MAX_VERTICES];
}GraphType;

int selected[MAX_VERTICES];
int distance[MAX_VERTICES];

// 최소 dist[v] 값을 갖는 정점을 반환
int get_min_vertex(int n){
    int v, i;
    for (i = 0; i < n; i++){
        // 아직 선택 되지 않은 정점을 찾아 해당 정점의 값을 v에 복사.
        if(!selected[i]){
            v = i;
            break;
        }
    }
    for(i = 0; i < n; i++){
        
        // 아직 선택 되지 않은 정점 중 distance가 가장 작은 값을 가진 정점을 v에 복사.
        if(!selected[i] && (distance[i] < distance[v]))
            v = i;
    }
    // 가장 작은 값을 가진 distance의 정점을 반환.
    return (v);
}

void prim(GraphType *g, int s){
    int i, u, v;
    // distance[] 초기화
    for(u = 0; u < g->n; u++){
        distance[u] = INF;
    }
    distance[s] = 0;    // 시작 정점의 거리 == 0;
    for(i = 0; i < g->n; i++){
        u = get_min_vertex(g->n);
        selected[u] = TRUE;
        if(distance[u] == INF) return;
        printf("정점 %d 추가\n", u);
        for(v = 0; v < g->n; v++){
            if(g->weight[u][v] != INF){
                if(!selected[v] && g->weight[u][v] < distance[v]){
                    distance[v] = g->weight[u][v];
                }
            }
        }
    }
}

int main(void) {
	GraphType g = { 7, 
	{ { 0, 29, INF, INF, INF, 10, INF },
	{ 29,  0, 16, INF, INF, INF, 15 },
	{ INF, 16, 0, 12, INF, INF, INF },
	{ INF, INF, 12, 0, 22, INF, 18 },
	{ INF, INF, INF, 22, 0, 27, 25 },
	{ 10, INF, INF, INF, 27, 0, INF },
	{ INF, 15, INF, 18, 25, INF, 0 } }
	};
	prim(&g, 0);
	return 0;
}

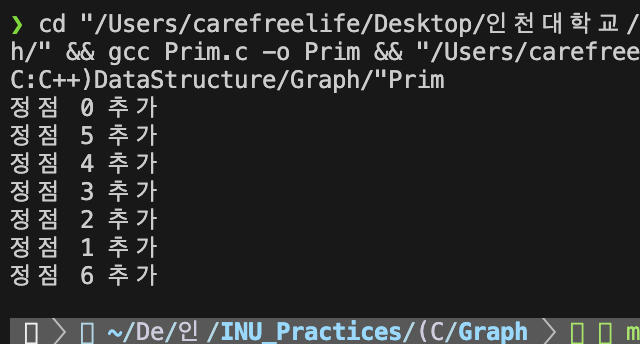
Prim 알고리즘 실행 결과

Prim 알고리즘의 분석

주 반복문이 정점의 수 n 만큼 반복, 내부 반복문이 n번 반복하므로

Prim 알고리즘은 O(n^2)의 복잡도를 가진다.

Kruskal VS Prim

Kruskal

간선을 기반으로 하는 알고리즘.

이전 단계에서 만들어진 신장 트리와 상관 없이 사이클이 없는 조건 하에 무조건 최저 간선만을 선택.

희소 그래프에 유리

O(e * log_2 e)

Prim

정점을 기반으로 하는 알고리즘.

이전 단계에서 만들어진 신장 트리를 확장해 나가는 방식.

밀집 그래프에 유리

O(n^2)

최대한의 설명을 코드 블럭 내의 주석으로 달아 놓았습니다.

혹시 이해가 안가거나 추가적인 설명이 필요한 부분, 오류 등의 피드백은 언제든지 환영합니다!

긴 글 읽어주셔서 감사합니다. 포스팅을 마칩니다.

처음으로~

참고: C언어로 쉽게 풀어쓴 자료구조 <개정 3판> 천인국, 공용해, 하상국 지음

Task Lists

신장 트리 (Spanning Tree) 란?
최소 비용 신장 트리 (MST : Minimum Spanning Tree) 란?
Kruskal 의 MST 알고리즘
(Kruskal) union - find 연산
Prim 의 MST 알고리즘
Kruskal VS Prim

Twitter Facebook LinkedIn

Chae Seungmin

Data Structure - 그래프 (Graph) (2) - Kruskal VS Prim

신장 트리 (Spanning Tree) 란?

최소 비용 신장 트리 (MST : Minimum Spanning Tree) 란?

Kruskal 의 MST 알고리즘

(Kruskal) union - find 연산

Prim 의 MST 알고리즘

Kruskal VS Prim

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)

※블로그 이전 안내※

Chae Seungmin

신장 트리 (Spanning Tree) 란?

최소 비용 신장 트리 (MST : Minimum Spanning Tree) 란?

Kruskal 의 MST 알고리즘

(Kruskal) union - find 연산

Prim 의 MST 알고리즘

Kruskal VS Prim

Task Lists

Comments

You May Also Enjoy

[Spring Basic] Spring - 컴포넌트 스캔 (Component Scan) 이란 ?

[2024 INU CSE 졸업작품] Smart Barricade: 우회전 교통사고 방지를 위한 전자 방지턱 시스템 (Spring Boot, Thymeleaf, Docker, Kafka, YoloV8, OpenCV)

[Capstone Design] Docker 통해서 Kafka, ZooKeeper 1시간 만에 사용해보기 (매우 간단, M1 Mac)

[Capstone Design] 스마트 방지턱 - 실시간 객체 탐지 및 속력 구하기 (YOLOv8, Supervision)