Python : 정렬 (Sort)의 개념 및 종류: 선택 정렬 / 삽입 정렬 / 합병 정렬 / 버블 정렬 / 자연 합병 정렬
정렬 문제의 정의
데이터를 특정 순서에 따라 나열하는 문제
- [3, 5, 2, 4] -> [2, 3, 4, 5]
전통적으로 컴퓨터 공학에서 많이 다루어지는 중요한 문제.
- 정렬되어 있다는 특성 자체로 효율적인 데이터의 처리를 할 수 있게 된다.
- 여러 정렬 방법 / 알고리즘이 존재하며, 각각의 해결 방법마다 시간 및 공간적 특성이 다르다.
-> 알고리즘 분석을 연습하기에 용이하다.
정렬 알고리즘 1. 선택 정렬 (Selection Sort)
- 리스트에서 가장 작은 원소를 선택하여 새로운 리스트에 추가하는 방식
- 리스트의 모든 원소가 선택 될 때까지 반복.
// pseudo code def selection_sort(s): while s != [], // 반복 조건 : list 가 공백 상태가 될 때까지 smallest ← min(s), s에서 min(s)를 제거한다. return [smallest]+selection_sort(s) //smallest와 s를 차례로 나란히 붙여 반환. if s == [], // 종료 조건 : 리스트가 공백이 되면 정렬할 필요가 없으므로 [] 반환
def selection_sort(l):
while l != []:
smallest = min(l)
l.remove(smallest)
return [smallest] + selection_sort(l)
if l == []:
return []
if __name__ == '__main__':
print(selection_sort([1, 5, 6, 7, 3, 5, 6, 4]))
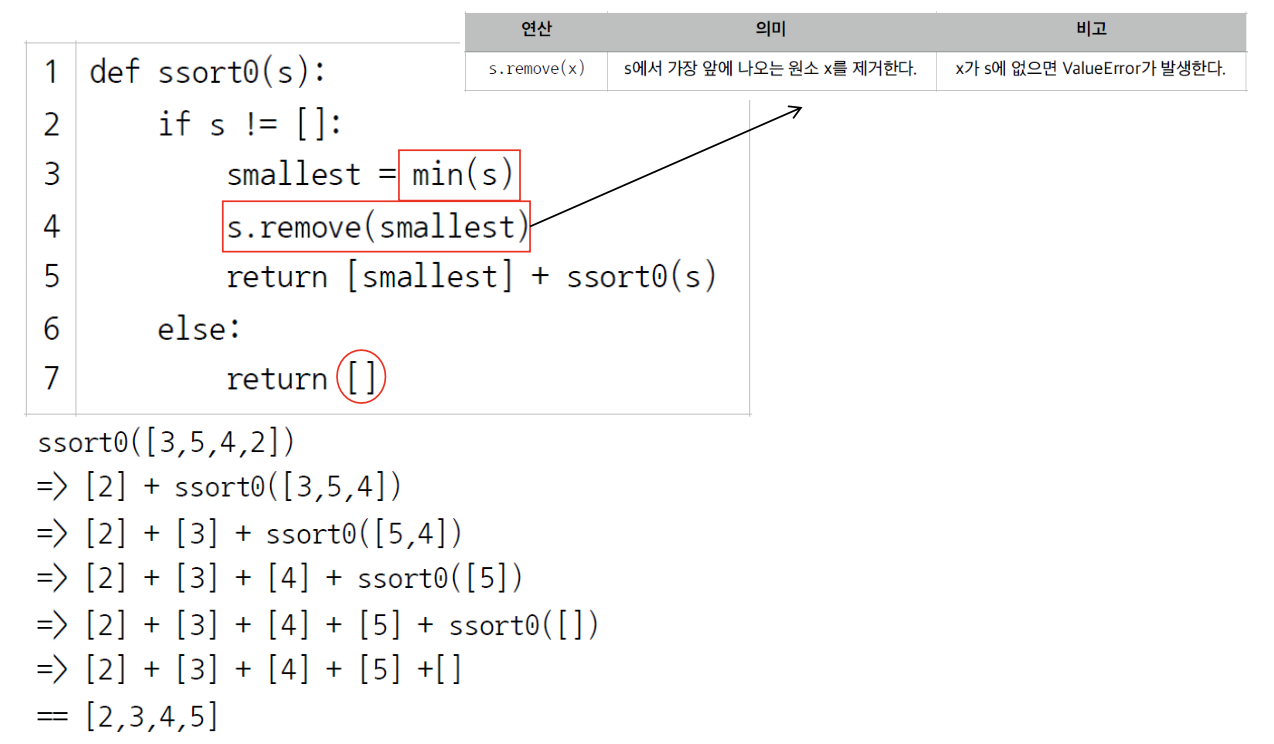
선택 정렬(Selection Sort)의 실행 결과선택 정렬의 구현 및 동작 과정
선택 정렬(Selection Sort)의 동작 과정꼬리 재귀 함수로의 변형
# 1단계 (결과를 저장해나갈 def loop 추가): def ssort(s): def loop(s, ss): if s != []: smallest = mis(s) s.remove(smallest) return loop(s, ss+[smallest]) else: return ss return loop(s, []) # 2단계 (완성): def ssort(s): def loop(s, ss): if s != []: smallest = min(s) s.remove(smallest) ss.append(smallest) return loop(s, ss) else: return ss return loop(s, []) # 3단계(선택 : 꼬리재귀 -> 반복문으로 변형) def ssort(s): ss = [] while s != []: smallest = min(s) s.remove(smallest) ss.append(smallest) return ss
정렬 알고리즘 2. 삽입 정렬 (Insert Sort)
- 리스트의 모든 요소들을 순차적으로 진행해가면서 각각 적절한 위치에 삽입하는 정렬 방식
- 리스트의 모든 원소가 선택될 때까지 반복.
# pseudo code - 삽입 정렬 (Insertion Sort)
정수 리스트 s를 정렬하려면
- (반복조건) s != [],
s의 후미 리스트인 s[1:] 를 정렬하여 ss 라고 한다.
정렬된 리스트 ss의 적당한 위치에 s의 선두원소인 s[0]를 끼워서 반환
- (종료조건) s == [], 정렬할 필요가 없으므로 그대로 반환
삽입 정렬의 구현 및 동작 과정
삽입 정렬의 구현 및 동작 과정
정렬 알고리즘 3. 합병 정렬 (Merge Sort)
리스트를 요소가 하나가 될 때까지 반으로 분할.
- 이후 요소들을 적절한 위치에 삽입하며 합병하여 정렬
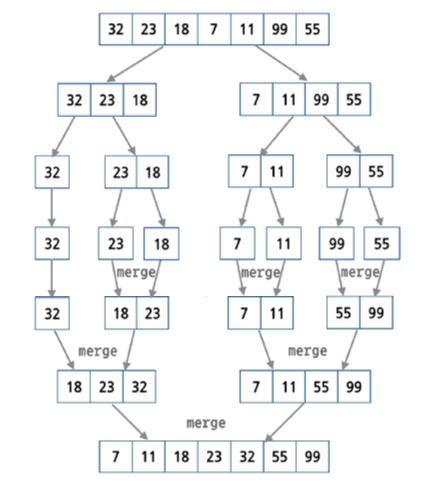
합병 정렬의 동작 과정
# 합병 정렬에서 메인이 되는 merge 함수.
# 함수 내에서 리스트를 분할하고, 적절한 위치에 삽입하여 정렬한다.
def merge(left, right):
if left != [] and right != []:
if left[0] <= right[0]:
return [left[0]] + merge(left[1:], right)
else:
return [right[0]] + merge(left, right[1:])
else:
return left + right
# merge 함수를 이용하여 합병 정렬 구현
def msort(s):
if len(s) > 1:
mid = len(s) // 2
return merge(msort(s[:mid]), msort(s[mid:]))
else:
return s
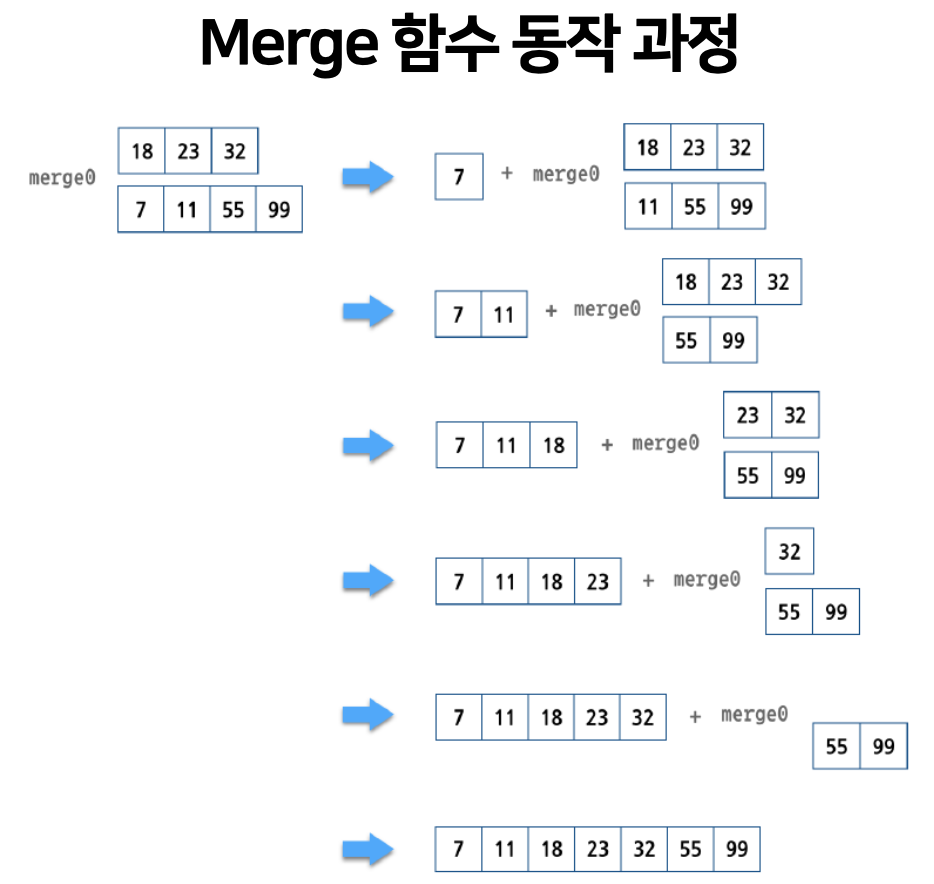
Merge 함수 동작 과정
Merge 함수 동작 과정
정렬 알고리즘 4. 버블 정렬 (Bubble Sort)
Step
1. 리스트의 제일 끝에서부터 인접한 두 요소를 비교하여 교환 정렬.
- 현재 검사하는 요소중 최소 값을 제일 앞으로.
2. 과정 1을 요소의 수 만큼 반복 -> 최종 정렬 완료
제자리 정렬 (in-place sort)
- 추가 공간(메모리)을 사용하지 않고 자체적으로 교환 정렬
- 버블 정렬은 리스트 내부 요소 간의 교환을 통한 정렬을 하기에 제자리 정렬이다.
- 선택, 삽입, 합병 정렬은 정렬의 중간 과정을 저장할 추가적인 공간을 필요로 함.
- 제자리 정렬이 아니다.
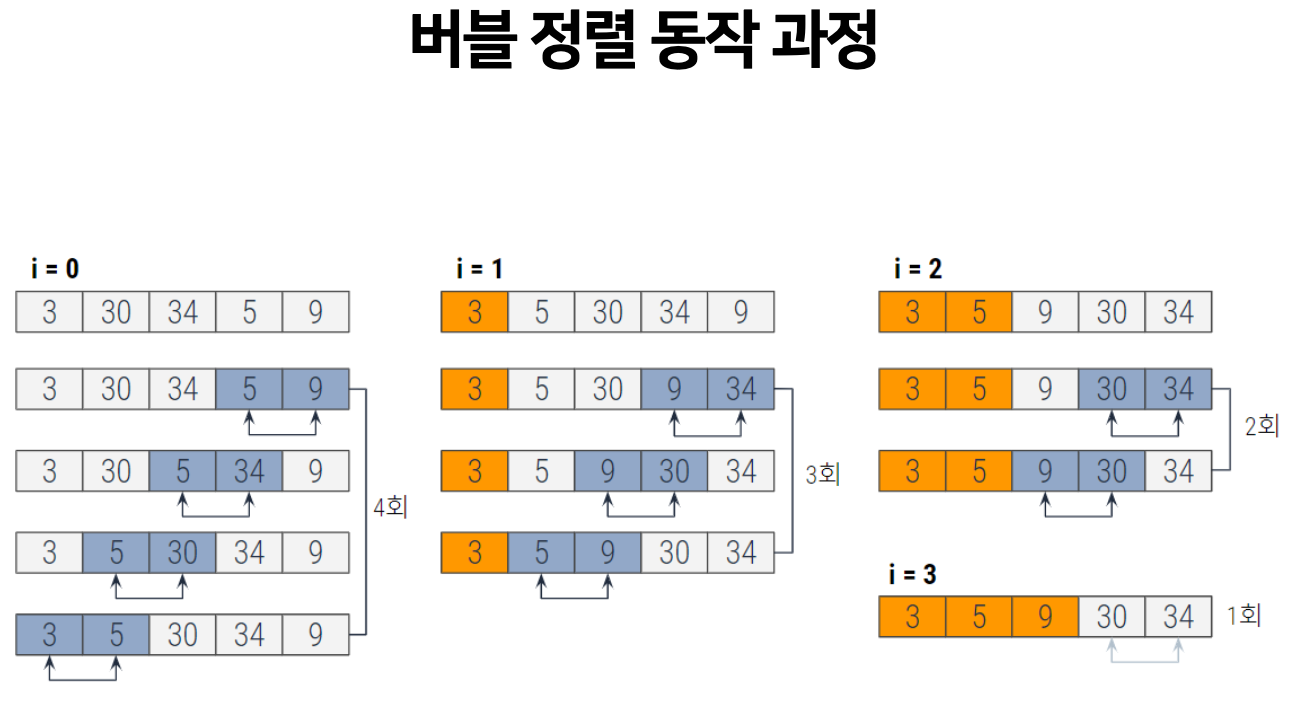
버블 정렬의 동작 과정
버블 정렬 동작 과정
# 버블 정렬의 구현
# 요소의 개수 만큼 반복
for k in range(len(l)):
# k는 1씩 증가하는데, 이는 한번 반복 후 리스트 앞 쪽부터 정렬된 요소를 제외하는 것을 의미.
# 리스트의 마지막 요소부터 시작, 리스트의 앞 쪽 부터 정렬된 요소 k개 만큼 제외한 위치까지 반복
for idx in range(len(l) - 1, k, -1):
# 만약 현재 요소가 자신보다 앞에 위치한 요소보다 작을 경우
if l[idx] < l[idx - 1]:
# 두 요소를 교환.
l[idx - 1], l[idx] = l[idx], l[idx - 1]
최대한의 설명을 코드 블럭 내의 주석으로 달아 놓았습니다.
혹시 이해가 안가거나 추가적인 설명이 필요한 부분, 오류 등의 피드백은 언제든지 환영합니다!
긴 글 읽어주셔서 감사합니다. 포스팅을 마칩니다.
Task Lists
- 정렬 문제의 정의
- 정렬 알고리즘 1. 선택 정렬 (Selection Sort)
- 정렬 알고리즘 2. 삽입 정렬 (Insert Sort)
- 정렬 알고리즘 3. 합병 정렬 (Merge Sort)
- 정렬 알고리즘 4. 버블 정렬 (Bubble Sort)






Comments